强化学习——价值学习中的DQN
文章目录
- 前言
- DQN算法
-
- 损失函数推导
- 训练DQN
- 训练DQN的技巧
-
- 优先经验回放数组
- 缓解高估问题
-
- 自举造成的高估问题
- 最大化造成的高估问题
- 双DQN
前言
本文为《深度强化学习》的阅读笔记,如有错误,欢迎指出
DQN算法
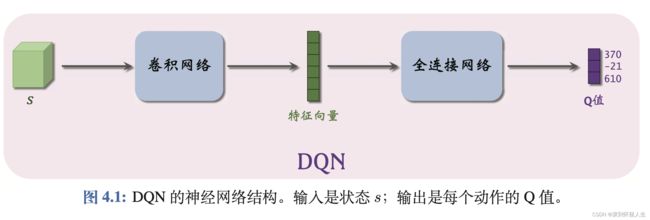
DQN算法通过神经网络拟合最优动作价值函数 Q ∗ ( s t , a t ) Q_*(s_t,a_t) Q∗(st,at),神经网络结构如下,输入为状态s,输出为每个动作的动作价值函数 Q ∗ ( s t , a t ) Q_*(s_t,a_t) Q∗(st,at)的值,即Q值, ∗ * ∗表示最优策略,有多少个动作,就有多少个输出,DQN处理离散动作空间。
损失函数推导
DQN的拟合目标为最优贝尔曼方程,其数学表达式为
Q ∗ ( s t , a t ) = E S t + 1 [ R t + γ max A Q ∗ ( S t + 1 , A ) ∣ S t = s t , A t = a t ] Q_{*}(s_t,a_t)=E_{S_{t+1}}[R_t+\gamma \max_{A}Q_{*}(S_{t+1},A)|S_t=s_t,A_t=a_t] Q∗(st,at)=ESt+1[Rt+γAmaxQ∗(St+1,A)∣St=st,At=at]
其中 R t R_t Rt为智能体在状态 s t s_t st做出动作 a t a_t at后,环境返回的奖励, γ \gamma γ为回报的折扣率,是一个超参数,其推导如下:


DQN的拟合目标可看成回归问题,则损失函数为均方误差,数学表达式为
L = 1 2 [ Q ∗ ( s t , a t ) − ( E S t + 1 [ R t + γ max A Q ∗ ( S t + 1 , A ) ∣ S t = s t , A t = a t ] ) ] 2 L=\frac{1}{2}[Q_{*}(s_t,a_t)-(E_{S_{t+1}}[R_t+\gamma \max_{A}Q_{*}(S_{t+1},A)|S_t=s_t,A_t=a_t])]^2 L=21[Q∗(st,at)−(ESt+1[Rt+γAmaxQ∗(St+1,A)∣St=st,At=at])]2
对于上式可以使用蒙特卡洛近似,假设现有一个四元组( s t , a t , r t , s t + 1 s_t,a_t,r_t,s_{t+1} st,at,rt,st+1),则有
L = 1 2 [ Q ∗ ( s t , a t ) − ( E S t + 1 [ R t + γ max A Q ∗ ( S t + 1 , A ) ∣ S t = s t , A t = a t ] ] ) ] 2 ≈ 1 2 [ Q ∗ ( s t , a t ) − [ r t + γ max A Q ∗ ( s t + 1 , A ) ] ] 2 \begin{aligned} L&=\frac{1}{2}[Q_{*}(s_t,a_t)-(E_{S_{t+1}}[R_t+\gamma \max_{A}Q_{*}(S_{t+1},A)|S_t=s_t,A_t=a_t]])]^2\\ &\approx \frac{1}{2}[Q_{*}(s_t,a_t)-[r_t+\gamma \max_A Q_{*}(s_{t+1},A)]]^2 \end{aligned} L=21[Q∗(st,at)−(ESt+1[Rt+γAmaxQ∗(St+1,A)∣St=st,At=at]])]2≈21[Q∗(st,at)−[rt+γAmaxQ∗(st+1,A)]]2
上式中的 Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at)和 max A Q ∗ ( s t + 1 , A ) \max_A Q_{*}(s_{t+1},A) maxAQ∗(st+1,A)均可通过DQN计算
训练DQN
DQN的具体训练流程为
-
收集训练数据,用任意策略控制智能体与环境进行交互,从而获得一系列四元组( s t , a t , r t , s t + 1 s_t,a_t,r_t,s_{t+1} st,at,rt,st+1),将这些四元组存储起来,构成经验回放数组。经验回放数组的大小为超参数,一般大小为 1 0 5 1 0 6 10^5~10^6 105 106,使用的策略一般为
a t = { arg max a Q ( s t , a ) , 概 率 为 1 − α 均 匀 抽 取 动 作 , 概 率 为 α \begin{aligned} a_t=\left\{\begin{matrix} & \argmax_a Q(s_t,a),概率为1-\alpha\\ & 均匀抽取动作,概率为\alpha \end{matrix}\right. \end{aligned} at={aargmaxQ(st,a),概率为1−α均匀抽取动作,概率为α
α \alpha α为超参数,Q(s_t,a)可以是随机初始化的神经网络 -
从经验回放数组中抽取一个四元组( s t , a t , r t , s t + 1 s_t,a_t,r_t,s_{t+1} st,at,rt,st+1),计算 Q ( s t , a t ) Q(s_t,a_t) Q(st,at)、 max A Q ( S t + 1 , A ) \max_{A}Q(S_{t+1},A) maxAQ(St+1,A)
-
计算损失函数,进行反向传播
上述流程也可改成批量梯度的训练方式,此时从经验回放数组中抽取 N N N个四元组,进行反向传播计算。
训练DQN的技巧
优先经验回放数组
经验回放数组均匀抽取四元组,优先经验回放数组非均匀抽取四元组,损失函数越大的四元组,被抽取的概率越大,直观理解,对于错误程度较大的样本,应该多训练,以减少错误程度。设四元组( s i , a i , r i , s i + 1 s_i,a_i,r_i,s_{i+1} si,ai,ri,si+1)的损失函数为 ∣ δ i ∣ |\delta_i| ∣δi∣,对 ∣ δ ∣ |\delta| ∣δ∣进行降序排序,每个四元组被抽取的概率为
p i = 1 r a n k ( i ) p_i=\frac{1}{rank(i)} pi=rank(i)1
r a n k ( i ) rank(i) rank(i)为 ∣ δ i ∣ |\delta_i| ∣δi∣的序号,更新完DQN后,需要更新经验回放数组中的对应四元组的 ∣ δ i ∣ |\delta_i| ∣δi∣。对于抽样频率较高的样本,更新次数较多,应该施加较小的学习率,反之,应该施加较大的学习率,优先经验回放数组将四元组( s i , a i , r i , s i + 1 s_i,a_i,r_i,s_{i+1} si,ai,ri,si+1)的学习率 a i a_i ai设置为
a i = α ( b ∗ p j ) β a_i=\frac{\alpha}{(b*p_j)^\beta} ai=(b∗pj)βα
b b b为经验回放数组的大小, α \alpha α为基础学习率, β \beta β为(0,1)之间的超参数。
缓解高估问题
自举造成的高估问题
DQN的损失函数为
L ≈ 1 2 [ Q ∗ ( s t , a t ) − [ r t + γ max A Q ∗ ( s t + 1 , A ) ] ] 2 \begin{aligned} L\approx \frac{1}{2}[Q_{*}(s_t,a_t)-[r_t+\gamma \max_A Q_{*}(s_{t+1},A)]]^2 \end{aligned} L≈21[Q∗(st,at)−[rt+γAmaxQ∗(st+1,A)]]2
Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at)和 max A Q ∗ ( s t + 1 , A ) \max_A Q_{*}(s_{t+1},A) maxAQ∗(st+1,A)均由神经网络自己估计,如果神经网络计算的 max A Q ∗ ( s t + 1 , A ) \max_A Q_{*}(s_{t+1},A) maxAQ∗(st+1,A)比真实的动作价值函数高,由于 Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at)用于逼近 r t + γ max A Q ∗ ( s t + 1 , A ) r_t+\gamma\max_A Q_{*}(s_{t+1},A) rt+γmaxAQ∗(st+1,A),这种高估现象会导致 Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at)的取值也变高,即高估从 max A Q ∗ ( s t + 1 , A ) \max_A Q_{*}(s_{t+1},A) maxAQ∗(st+1,A)传播至 Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at),从而导致DQN针对某些状态和动作给出过高的估计(高估是不均匀的),可能导致智能体做出一些错误的行为。
最大化造成的高估问题
假设现有一系列随机变量 X 1 、 X 2 、 X 3 、 . . . X n X_1、X_2、X_3、... X_n X1、X2、X3、...Xn,往随机变量中添加一些均值为0的噪声 ϵ \epsilon ϵ得到随机变量 Z 1 、 Z 2 、 Z 3 、 . . . Z n Z_1、Z_2、Z_3、... Z_n Z1、Z2、Z3、...Zn,则有下列不等式
E ϵ [ max ( Z 1 , Z 2 , Z 3 , . . . , Z n ) ] ≥ max ( X 1 , X 2 , X 3 . . . . X n ) E_{\epsilon}[\max(Z_1,Z_2,Z_3,...,Z_n)]\geq \max(X_1,X_2,X_3....X_n) Eϵ[max(Z1,Z2,Z3,...,Zn)]≥max(X1,X2,X3....Xn)
设DQN的输出 Q ( s t , a t ) Q(s_t,a_t) Q(st,at)为真实价值函数 Q ∗ ( s t , a t ) Q_{*}(s_t,a_t) Q∗(st,at)与均值为0的噪声之和,则有
E ϵ [ max a t ( Q ( s t , a t ) ) ] ≥ max a t Q ∗ ( s t , a t ) E_\epsilon[\max_{a_t}(Q(s_t,a_t))]\geq \max_{a_t} Q_{*}(s_t,a_t) Eϵ[atmax(Q(st,at))]≥atmaxQ∗(st,at)
注意上式是噪声 ϵ \epsilon ϵ的期望。DQN的优化目标为:
Q ( s t , a t ) = r t + γ max A Q ( s t + 1 , A ) Q(s_t,a_t)=r_t+\gamma \max_A Q(s_{t+1},A) Q(st,at)=rt+γAmaxQ(st+1,A)
在有噪声情况下,则有
E ϵ [ Q ( s t , a t ) ] = r t + γ E ϵ [ max A Q ( s t + 1 , A ) ] ≥ r t + γ max a t Q ∗ ( s t + 1 , a t ) E_\epsilon[Q(s_t,a_t)]=r_t+\gamma E_\epsilon[\max_A Q(s_{t+1},A)]\geq r_t+\gamma \max_{a_t} Q_{*}(s_{t+1},a_t) Eϵ[Q(st,at)]=rt+γEϵ[AmaxQ(st+1,A)]≥rt+γatmaxQ∗(st+1,at)
即在有噪声的情况下(通常情况下都有噪声),且模型参数变动情况不大情况下,DQN优化的是最优贝尔曼方程的上界,从而使DQN对某些动作和状态做出过高估计,导致智能体做出错误动作。
双DQN
双DQN引入了目标网络,设目标网络与DQN的参数分别为 w n o w − 、 w n o w w^-_{now}、w_{now} wnow−、wnow,则双DQN的具体更新步骤为
- 从经验回放数组中抽取四元组 ( s t , a t , s t + 1 , r t ) (s_t,a_t,s_{t+1},r_t) (st,at,st+1,rt)
- 对DQN进行前向传播, q ^ t = Q ( s t , a t ; w n o w ) \hat q_t=Q(s_t,a_t;w_{now}) q^t=Q(st,at;wnow)
- 选择动作 : a ∗ = arg max a Q ( s t + 1 , a ; w n o w ) a^*=\argmax_{a} Q(s_{t+1},a;w_{now}) a∗=aargmaxQ(st+1,a;wnow)
- 利用目标网络计算: q ^ t + 1 = Q ( s t + 1 , a ∗ ; w n o w − ) \hat q_{t+1}= Q(s_{t+1},a^*;w_{now}^-) q^t+1=Q(st+1,a∗;wnow−),由于动作来自于DQN,则有 m a x a Q ( s t + 1 , a ; w n o w − ) ≥ Q ( s t + 1 , a ∗ ; w n o w − ) max_{a} Q(s_{t+1},a;w_{now}^-)\geq Q(s_{t+1},a^*;w_{now}^-) maxaQ(st+1,a;wnow−)≥Q(st+1,a∗;wnow−),从而避免最大化导致的高估问题,并且使用目标网络计算 q ^ j + 1 \hat q_{j+1} q^j+1,切断了自举导致的高估传播,即DQN的高估不会从 Q ( s t + 1 , a t + 1 ; w n o w ) Q(s_{t+1},a_{t+1};w_{now}) Q(st+1,at+1;wnow)传递至 Q ( s t , a t ; w n o w ) Q(s_{t},a_{t};w_{now}) Q(st,at;wnow)
- 计算loss: 1 2 [ q ^ t − [ r t + γ q ^ t + 1 ] ] 2 \frac{1}{2}[\hat q_t-[r_t+\gamma \hat q_{t+1}]]^2 21[q^t−[rt+γq^t+1]]2,进行反向传播