二维Poisson方程五点差分格式与Python实现

• 最近没怎么写新文章，主要在学抽象代数
• 下学期还有凸分析
• 好累的一学期
• 哦对，我不是数学系的，我是物理系的。而且博主需要澄清一下，博主没有对象，至少现在还没有。

---

---

• 好，兄弟们，好习惯，先上代码后说话！

Python 实现

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import scipy.sparse as ss
from scipy.sparse.linalg import spsolve

class PDE2DModel:
    #均应该传入一个一维二元数组，表示起止值
    def __init__(self,x,y):
        assert len(x)==len(y)==2,"ERROR:UNEXPECTED SV and EV!!"
        self.x = x
        self.y = y

    #hx表示X上的步长
    #hy表示Y上的步长
    def space_grid(self,hx,hy):
        M = int(round((self.x[1]-self.x[0])/hx,0))
        N = int(round((self.y[1]-self.y[0])/hy,0))
        assert M==N>=3,"至少网格数是合理的"
        X = np.linspace(self.x[0],self.x[1],M+1)
        Y = np.linspace(self.y[0],self.y[1],N+1)
        return M,N,X,Y

    def f(self,X,Y):
        return 6*X*Y**3+6*X**3*Y+np.e**X*np.sin(Y)-np.e**X*np.sin(Y)

    def solution(self,X,Y):
        return np.e**X*np.sin(Y)-X**3*Y**3

    #左边界
    def left(self,Y):
        return np.sin(Y)
    #右边界
    def right(self,Y):
        return np.e**3*np.sin(Y)-27*Y**3
    #上边界
    def up(self,X):
        return np.sin(1)*np.e**X-X**3
    #下边界
    def down(self,X):
        return 0*X

#解算核心
def NDM5_2D(PDE2DModel,hx,hy):
    M,N,X0,Y0 = PDE2DModel.space_grid(hx,hy)
    Y,X = np.meshgrid(Y0,X0)
##    print("X0",X0)
##    print("Y0",Y0)
##    #数值结果保存在U中 从0到N共N+1个
##    print("M",M)
##    print("N",N)
    U = np.zeros((M+1,N+1))
    U[0,:]  = PDE2DModel.left(Y0)
    U[-1,:] = PDE2DModel.right(Y0)
    U[:,0]  = PDE2DModel.down(X0)
    U[:,-1] = PDE2DModel.up(X0)

    D = np.diag([-1/(hy**2) for i in range(M-1)])
    C = np.zeros((N-1,N-1),dtype="float64")
    for i in range(N-1):
        C[i][i] = 2*(1/hx**2+1/hy**2)
        if i

---

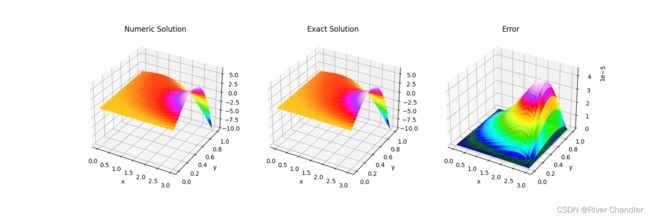
• 好习惯2,效果图

很好,接下去接着讲

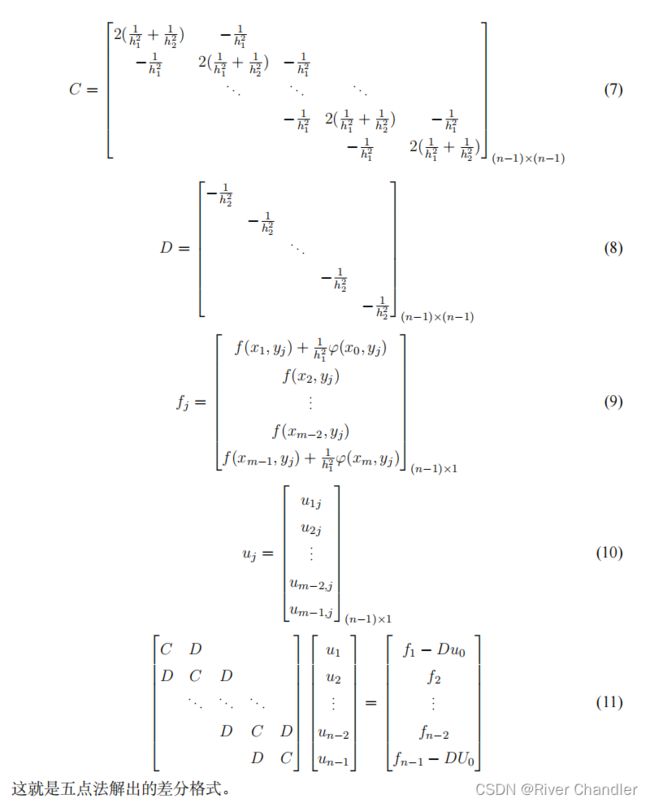
五点差分格式

•  这里我要用截图,截的我的小论文.没办法,CSDN写作太麻烦了,没有Latex好用.我记得这个好像可以调整,但我没学会

 

 很好,结束了.

注意事项

• 你在写代码的时候,容易犯几个错误.
• 在纸上图画出来了,然后呢,纸上是右手系,写进数组了,就忘了是啥系了!
• 比如:

    Y,X = np.meshgrid(Y0,X0)

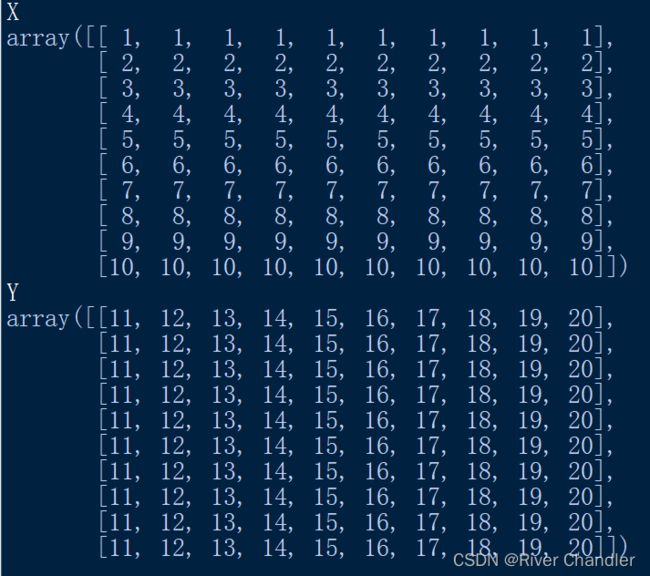
• 我们需要重点看一下np.meshgrid问题.这才是大家想要的数据结构.....

import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9,10])
y = np.array([11,12,13,14,15,16,17,18,19,20])

Y,X = np.meshgrid(y,x)

•  其实这个还涉及到稀疏矩阵的问题,稀疏矩阵解决不了的话,你的运算量会变得超大!一定要用系数矩阵优化才能解决问题!!

所以,优化之后!

用稀疏矩阵优化

import numpy as np
import scipy as sp
from scipy.sparse.linalg import spsolve
from scipy.sparse import csr_matrix,csc_matrix
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import scipy.sparse as ss
from scipy.sparse.linalg import spsolve
import  time

class PDE2DModel:
    def __init__(self):
        self.x = np.array([0,3])
        self.y = np.array([0,1])

    def space_grid(self,hx,hy):
        M = int(round((self.x[1]-self.x[0])/hx,0))
        N = int(round((self.y[1]-self.y[0])/hy,0))
        assert M==N>=3,"ERROR:UNECPECTED GRIDS M:"+str(M)+" N:"+str(N)
        X = np.linspace(self.x[0],self.x[1],M+1)
        Y = np.linspace(self.y[0],self.y[1],N+1)
        return M,N,X,Y

    def f(self,X,Y):
        return 6*X*Y**3+6*X**3*Y+np.e**X*np.sin(Y)-np.e**X*np.sin(Y)

    #左边界
    def left(self,Y):
        return np.sin(Y)
    #右边界
    def right(self,Y):
        return np.e**3*np.sin(Y)-27*Y**3
    #上边界
    def up(self,X):
        return np.sin(1)*np.e**X-X**3
    #下边界
    def down(self,X):
        return 0*X


def NDM5_2D(PDE2DModel,hx,hy):

    M,N,X0,Y0 = PDE2DModel.space_grid(hx,hy)
    Y,X = np.meshgrid(Y0,X0)

    U = np.zeros((M+1,N+1))
    U[0,:]  = PDE2DModel.left(Y0)
    U[-1,:] = PDE2DModel.right(Y0)
    U[:,0]  = PDE2DModel.down(X0)
    U[:,-1] = PDE2DModel.up(X0)

    D = np.diag([-1/(hy**2) for i in range(M-1)])
    C = np.zeros((N-1,N-1),dtype="float64")
    for i in range(N-1):
        C[i][i] = 2*(1/hx**2+1/hy**2)
        if i

Python技巧

map

• 水字数用,哥以后转战其他网站了.这个评分系统太恶心了.太恶心了.
• 其实有个很有趣的现象.没考过计算机二级的人觉得二级Python弱爆了.一点用没有,备考计算机二级Python的人觉得难暴了.......
• 挺好的,说不出话来......
• 其实我个人认为非专业人士考一次计算机二级有助于学习的,还可以水创新学分.真是想不通哪个SX想出的创新学分.不是,这个人啊,他创新,创新这个是用指标逼出来的吗?

f = lambda x:x+5
X = [1,2,3,4,5]
map(f,X)

Python自制警告

• Python 自制警告是很有必要的.
• 自制的警告与自制的错误不一样,不会打断程序运行(显然废话)

import warnings
a = 0
if a==0:
    warnings.warn("IGNORE!")
print(a+3)

Warning (from warnings module):
  File "C:\Users\LX\Desktop\新建 文本文档.py", line 34
    warnings.warn("IGNORE!")
UserWarning: IGNORE THIS WARNING!
3

Python matplotlib技巧

##import matplotlib
##import matplotlib.pyplot as plt
##from mpl_toolkits.mplot3d import Axes3D
##matplotlib.rcParams["font.sans-serif"] = ["SimHei"]
##matplotlib.rcParams["axes.unicode_minus"] = False
##
##import numpy as np
##
##x = np.linspace(1,2,6)
##y = np.linspace(3,9,13)
##Y,X = np.meshgrid(y,x)
##X2,Y2 = np.meshgrid(x,y)
##
##plt.figure(figsize=(15,5))
##ax1 = plt.subplot(121,projection="3d")
##ax2 = plt.subplot(122,projection="3d")
##
##ax1.set_title("Inverse order")
##ax2.set_title("Ordinary order")
##ax1.set_xlabel("x")
##ax2.set_xlabel("x")
##
##f = lambda x,y:x*2+y*3
##ax1.plot_surface(X,Y,f(X,Y))
##
##ax2.plot_surface(X2,Y2,f(X2,Y2))
##
##plt.show()