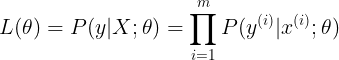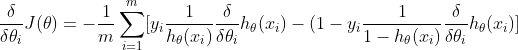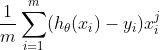机器学习——逻辑回归算法
文章目录
- 逻辑回归算法
-
- 逻辑回归概念
- Sigmoid函数
- 逻辑回归模型
- 代价函数
- 最终运用梯度下降求解
- 实验
- 总结
逻辑回归算法
首先明确一个概念,逻辑回归并不是解决回归问题,而是解决分类问题,它是通过训练数据中的正负例,学习样本特征得到标签之间的假设函数,是一种典型的线性分类器。
逻辑回归概念
面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证求解模型的好坏。
逻辑回归实际是一种分类方法,主要用于两分类问题,即输出只有两种,分别代表两个类别。用Sigmoid函数就可以让逻辑回归只能输出两种值。
Sigmoid函数
Logistic函数(或Sigmoid函数),函数形式为:
对应图形如下:
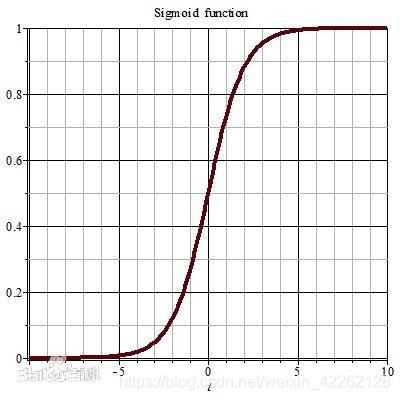
可以看出,Sigmoid函数是一个S型的曲线,它的取值在[0,1]之间,在远离0的地方函数值会很快接近0或1。可以思考,一个事件发生的概率是在0到1之间的,每一个概率都可以映射到函数的某一个值上,就可以归类为超过50%的概率更容易实现归一为1,低于50%的概率更不容易实现归一为0,这样就存在了只有0/1的二分类问题。
逻辑回归模型
逻辑回归模型所做的假设是:
![]()
可以发现,这里离将Sigmoid函数中的变量x换成了一个线性回归公式,组成了新的逻辑回归公式。
代价函数
逻辑回归算法也是用最大似然估计来学习的,所以单个样本的后验概率为:
![]()
这是一个二项分布的整合式,相当于当y取1时,式子取h(x),而当y取0时,式子取1-h(x)。那么整个样本的后验概率为:
转换成矩阵式,取对数可以得到对数似然度:
![]()
最终运用梯度下降求解
对数似然是越大越好的,求梯度下降需要在式子前边加负号,转变为求解最小值。所以求偏导的式子可以表示为:
最终可以化简为:
可以说,沿梯度负方向选择一个较小的步长可以保证代价函数是减小的,另一方面代价函数是凸函数,可以保证找到的局部最优值是全局最优。
实验
利用梯度下降实现逻辑回归模型,下述代码用于求解y=2x1+x2+3,即使用梯度下降法求解y=ax1+bx2+c中参数a、b、c的最优值:
import numpy as np
import matplotlib.pyplot as plt
rate = 0.001
x_train = np.array([[1,2], [2,1], [2,3], [3,5], [1,3], [4,2], [7,3], [4,5], [11,3], [8,7]])
y_train = np.array([7,8,10,14,8,13,20,16,28,26])
x_test = np.array([[1,4], [2,2], [2,5], [5,3], [1,5], [4,1]])
a = np.random.normal()
b = np.random.normal()
c = np.random.normal()
def h(x):
return a * x[0] + b * x[1] + c
for i in range(100):
sum_a = 0
sum_b = 0
sum_c = 0
for x, y in zip(x_train, y_train):
for xi in x:
sum_a = sum_a + rate * (y - h(x)) * xi
sum_b = sum_b + rate * (y - h(x)) * xi
a = a + sum_a
b = b + sum_b
c = c + sum_c
plt.plot([h(xi) for xi in x_test])
print(a)
print(b)
print(c)
result = [h(xi) for xi in x_train]
print(result)
result = [h(xi) for xi in x_test]
print(result)
plt.show()
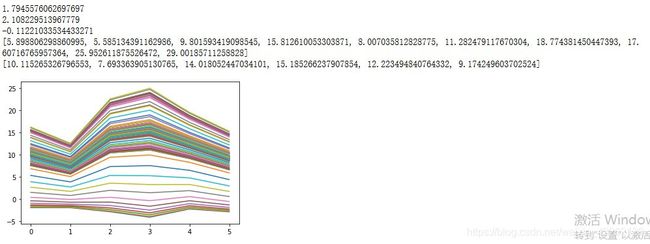
算法求得的a、b、c的最优值和效果图如图所示:
总结
逻辑回归具有一些优点:形式简单,模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响,某个特征的权重值比较高,那么这个特征最后对结果的影响会比较大。训练速度较快。分类的时候,计算量仅仅只和特征的数目相关,训练的速度可以通过堆机器进一步提高,这样我们可以在短时间内迭代好几个版本的模型。
但是逻辑回归本身也有许多的缺点:准确率并不是很高。因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布。很难处理数据不平衡的问题。举个例子:如果我们对于一个正负样本非常不平衡的问题,比如正负样本比 10000:1,我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器,它对正负样本的区分能力不会很好。处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下,只能处理线性可分的数据,或者进一步说,处理二分类的问题 。