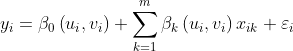ArcGIS中GWR模型的构建
- 介绍
回归分析分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系。线性回归是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。在传统回归分析中,如最小二乘模型(OLS),基本假设是自变量与因变量的关系在整个地区保持稳定。一般线性回归都是全局的。
地理加权回归是一种空间分析技术,广泛应用于地理学及涉及空间模式分析的相关学科研究。在空间分析中,观测数据一般按照给定的地理位置作为采样单元进行采样,随着地理位置的变化,变量间的关系或者结构会发生改变,这种因为地理位置的变化,而引起的变量间关系或结构的变化称之为空间非平稳性。空间非平稳性普遍存在于空间数据中,如不同省份的AIDS发病率、湖泊不同深度TN含量、城市工业区与非工业区PM2.5浓度等等。假如采用全局空间回归模型,便忽略了数据的空间位置属性,只反映平均意义下因变量与自变量的相关关系,而不能有效反映回归关系的空间非平稳性的特征。地理加权回归是对普通线性回归模型的扩展,将数据的空间位置嵌入到回归方程中,具有更高的准确性。
根据地理学第一定律,以不同数据点和回归点的空间距离得到一个连续的衰减函数。对各数据点赋予不同的权重,离得近的样点在计算时候占的权重更大,离得远的样点占的权重小。空间权重矩阵的常用计算方法有Gauss函数法和bi-square 函数法。确定空间权重矩阵而后建立局部区域的加权回归方程。形式如下:
![]()
其中(ui,vi)为第i个数据点的坐标;w(ui,vi)是地i个数据点的权重;βk(ui,vi)是第i个数据点上第k个回归参数,为空间地理位置函数。
2 数据
南昌市行政区划、南昌市停车场矢量数据和南昌市道路矢量数据。
3 ArcGIS操作
3.1 输入要素:
输入矢量数据。把需要使用的数据都合并到一个要素类中,每一个变量都有一列独立的数据,且不能出现空值。
3.2 输入因变量 有且只有一个因变量
3.3 输入自变量 至少一个自变量
3.4 输出结果
3.5 核的类型
工具提供两种核函数:
(1)FIXED :固定距离法,按照一定的距离选择带宽,创建核表面。
(2)ADAPTIVE :自适应法。按照要素样本分布的疏密,创建核表面,如果要素分布紧密,则核表面覆盖的范围小,反之则大。默认会使用固定方式,固定方式能够生成更加平滑的核表面。
3.6 带宽
此参数用于设定GWR的带宽。参数有三个选项:
(1)CV:通过交叉验证法来决定最佳带宽。
(2)AICc:通过最小信息准则来决定最佳带宽。
(3)BANDWIDTH_PARAMETER :指定宽度或者临近要素数目的方法。
3.7 距离(可选)
选择指定宽度时,自定义带宽的距离
3.8 临近要素的数目(可选)
选择核类型为自适应,核带宽为BANDWIDTH_PARAMETER时,此参数可用。默认数目为30,表示选择回归点周边的30个点作为核局部带宽中作为临近要素的点。
3.9 权重字段(可选):
对每个要素设置独立的权重。
3.10系数栅格的工作空间
生成各样本的各个自变量系数的栅格数据
4 分析
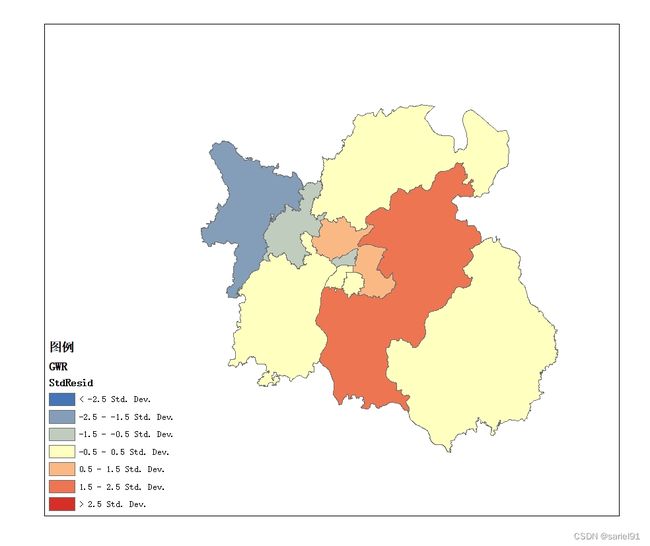
4.1 GWR结果图
生成图的数值是系数的标准误差。主要用来衡量每个系数估计值的可靠性。标准误差与实际系数值相比较小时,可信度高,较大时可能表示局部多重共线性存在问题。
4.2 GWR属性表
Observed F:因变量的观测值。
Condition Number:条件数,数值用于此诊断评估局部多重共线性。存在较强局部多重共线性的情况下,结果将变得不稳定。如果出现了大于 30 的条件数相关联,结果就可能是不可靠的。
Local R2:范围在 0.0 与 1.0 之间,表示局部回归模型与观测所得 y 值的拟合程度。值低则表示局部模型性能不佳。对 Local R2进行地图可视化,可以查看哪些位置 GWR 预测较准确,哪些位置预测不准确。
Predicted:对因变量的预测值,是由 GWR 计算所得的估计y 值。预测值越接近因变量的值表示拟合度越高。
Coefficient Intercept:截距,表示与Y轴的交点,截距为负表示观测值小于预测值。
Coefficient:各样本的各个自变量的系数。
Residual:残差,观测值与预测值的差。
Standard Error:标准误,衡量的是在用样本统计量去推断相应的总体参数(常见如均值、方差等)的时候,一种估计的精度。
Standard Error Intercept:标准误的截距,标准差与Y轴的交点。
Standard Error Coefficient:各自变量系数标准误。用于衡量每个系数估计值的可靠性。标准误与实际系数值相比较小时,可信度高。较大标准误差时,表示局部多重共线性存在问题。
Std. Residual:标准化残差。标准化残差的平均值为零,标准差为 1。在 ArcMap 中执行 GWR 时,将自动将标准化残差渲染为由冷色到暖色渲染的地图。超过2.5倍标准化残差的地方可能有问题。
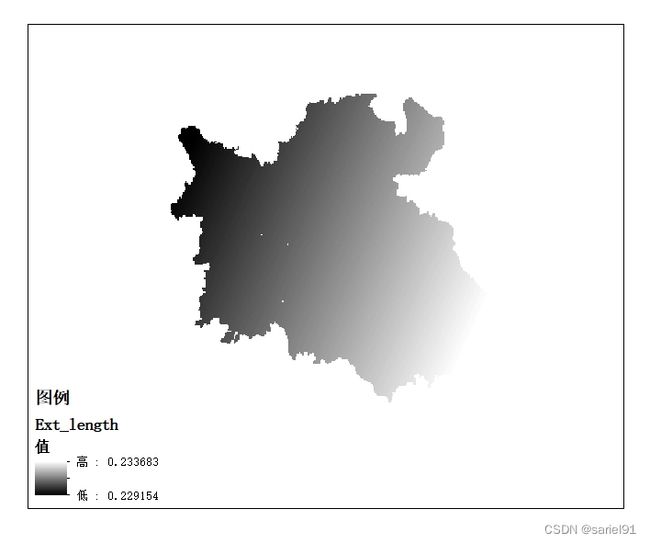
4.2 系数栅格图
各样本的各个自变量的系数(Coefficient)的栅格化,体现出的是变量在不同区域位置对因变量的作用的强弱。
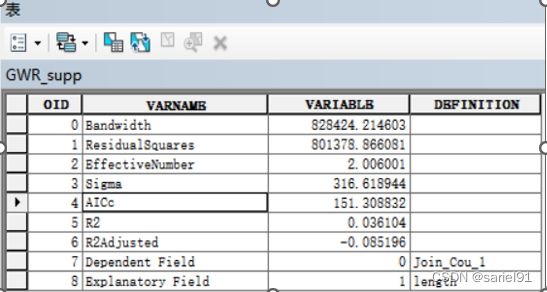
4.3 辅助表:
Bandwidth 或 Neighbors:是指用于各个局部估计的带宽或相邻点数目。它控制模型中的平滑程度。
ResidualSquares:指模型中的残差平方和(残差为观测所得 y 值与 GWR 模型所返回的 y 值估计值之间的差值)。此测量值越小,GWR 模型越拟合观测数据。
EffectiveNumber:值反映了拟合值的方差与系数估计值的偏差之间的折中,与带宽的选择有关。带宽接近无穷大时,每个观测值的地理权重都将接近 1,系数估计值与全局 OLS 模型的相应值将非常接近。对于较大的带宽,系数的有效数量将接近实际数量;局部系数估计值将具有较小的方差,但偏差将非常大。相反,带宽接近零时,每个观测值的地理权重都将接近零(回归点本身除外)。对于非常小的带宽,系数的有效数量为观测值的数量,局部系数估计值将具有较大方差但偏差较低。该有效数量用于计算多个诊断测量值。
Sigma:此值为正规化剩余平方和(剩余平方和除以残差的有效自由度)的平方根。它是残差的估计标准差。此统计值越小越好。Sigma 用于 AICc 计算。
AICc:这是模型性能的一种度量,有助于比较不同的回归模型。考虑到模型复杂性,具有较低 AICc 值的模型将更好地拟合观测数据。AICc 不是拟合度的绝对度量,但对于比较适用于同一因变量且具有不同解释变量的模型非常有用。如果两个模型的 AICc 值相差大于 3,具有较低 AICc 值的模型将被视为更佳的模型。
R2:R 平方是拟合度的一种度量。其值在 0.0 到 1.0 范围内变化,值越大越好。R2 计算的分母为因变量值平方和。向模型中再添加一个解释变量不会更改分母但会更改分子;这将出现改善模型拟合的情况(但可能为假象)。
R2Adjusted:由于上述 R2 值问题,校正的 R 平方值的计算将按分子和分母的自由度对它们进行正规化。这具有对模型中变量数进行补偿的效果,因此校正的 R2 值通常小于 R2 值。但是,执行此校正时,无法将该值的解释作为所解释方差的比例。
参考资料:
- 《白话空间统计:地理加权回归系列》——大虾卢
- 《地理加权回归基本理论与应用研究》——覃文忠
- 《ArcGIS与地理加权回归GWR》——公众号:一点规划
- 《地理加权回归简易总结》