空间自相关—莫兰指数
想起这个素材是因为读研时学过这门课...（啧，就这还敢说学过）前面大部分内容根据官方帮助文档自己整理，详细信息可参照Arcgis帮助文档，正好在看论文有份数据就借来练习了...
公众号原文链接，欢迎关注
空间自相关—莫兰指数莫兰指数 热点分析
https://mp.weixin.qq.com/s/QtymA6nrW9rpdMJYCjCZww
【莫兰指数】
莫兰指数分为全局莫兰指数（Global Moran's I）和局部莫兰指数（Local Moran's I），前者是Patrick Alfred Pierce Moran开发的空间自相关的度量；后者是美国亚利桑那州立大学地理与规划学院院长Luc Anselin 教授在1995年提出的。在Arcgis里分别是“空间自相关”与“聚类和异常值分析”工具。
通常情况，先做一个地区的全局莫兰指数，全局指数告诉我们空间是否出现了集聚或异常值。如果全局有自相关出现，接着做局部自相关，局部Moran'I会告诉我们哪里出现了异常值或者哪里出现了集聚。
【零假设与置信度】
在解释p值z得分前，需要了解一下这两个名词:
1.零假设：官方的解释是指进行统计检验时预先建立的假设。这个“零假设”的设立是为了去否定它的，空间统计中的零假设是指“统计的空间要素是随机分布的”，要去做的也就是去证明要素不是随机分布的，是呈现聚类或者离散分布的。
2.置信度与置信区间：比如我这个实验结论有95%的置信度，意义就是我有95%的把握拒绝零假设，证明零假设是错误的，是可以实现这个结果。置信区间是保证这个置信度的变量或参数的区间范围。区间越大猜中概率越大。
【Moran's I、P值、Z值】
Moran's I指数：它的范围在 -1.0 与 +1.0 之间。
Moran's I大于0时，表示数据呈现空间正相关，值越大空间相关性越明显；Moran's I小于0时，表示数据呈现空间负相关，值越小空间差异越大；Moran's I为0时，空间呈随机性。
解读莫兰指数的时候，需要有P值和Z得分来判定。他们两个要结合在一起看。
P值：表示概率，当p很小时，意味着所观测到的空间模式不太可能产生于随机过程（小概率事件），因此可以拒绝零假设。
Z得分：标准差倍数。如果工具返回的 z 得分为+2.5，我们就会说，结果是2.5倍标准差。记住标准差能反映一个数据集的离散程度，就可以了。
| z 得分（标准差） | p 值 | 置信度 |
| < -1.65 或> +1.65 |
< 0.10 | 90% |
| < -1.96 或> +1.96 |
< 0.05 | 95% |
| < -2.58 或> +2.58 |
< 0.01 | 99% |
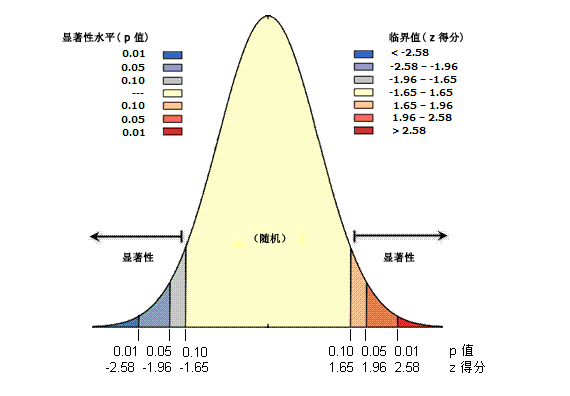
中间黄色部分为随机分布，右侧为集聚分布，左侧为离散分布。
在下面有P值与Z得分两行数值。在两端出现非常高或非常低（负值）的z得分，这些得分与非常小的 p 值关联。结合表格看：
假如P值＜0.01，且Z得分＞2.58，那么就落在图的最最最右边红色的区域，我们可以说有99%的把握要素是集聚分布的。对应的，如果P值＜0.01，且Z得分<-2.58，那么就落在图的最最最左边蓝色的区域，我们可以说有99%的把握要素是离散分布的。假如P值＜0.01，但Z得分<2.58，那么就表示不可以拒绝零假设，所表现出的模式很可能是随机空间过程产生的结果。还有一种情况，如果做出来的P值很小，Z得分的绝对值又很大，远超过两端，那么表明观测到的空间模式不可能是随机过程产生的结果。在这种情况下，可以拒绝零假设，并着手找出是什么可能导致数据出现具有统计显著性的空间结构。
【空间关系概念化】
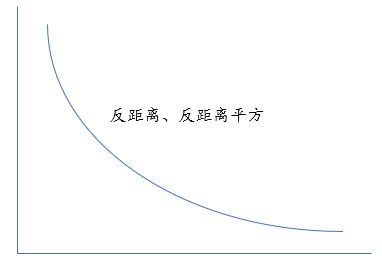
1.inverse_distance（反距离）：与远处的要素相比，附近的邻近要素对目标要素的计算的影响要大一些。
2.inverse_distance_squared（反距离平方）：与第一种相似，但它对距离反应更为敏感。所以这两种方法区别就在于附近邻近要素对目标要素的计算的影响有多大，特别大就第二种。
如果横坐标代表距离，纵轴代表影响力，那么随着距离增加，影响力就变得越来越小。这就是反距离。
3.fixed_diatance_band（距离范围影响）：将对邻近要素环境中的每个要素进行分析。在指定临界距离（距离范围或距离阈值）内的邻近要素将分配有值为 1 的权重，并对目标要素的计算产生重大影响。在指定临界距离外的邻近要素将分配值为零的权重，并且不会对目标要素的计算产生任何影响。其实就是在一定范围内的临近要素对目标要素影响力是一样的，不存在随距离增加而减小。
横轴代表距离，纵轴代表影响力，在到达蓝点之前，影响力不会随距离增加而衰减，都是一样的。而过了这个点就不会产生影响。
4.zone_of_indifference（无差别的区域）：在目标要素的指定临界距离（距离范围或距离阈值）内的要素将分配有值为1的权重，并且会影响目标要素的计算。一旦超出该临界距离，权重（以及邻近要素对目标要素计算的影响）就会随距离的增加而减小。
可以看做是“反距离”与“距离范围”的结合，在指定的范围内影响力都是一样的，超过后影响力便随着距离增加而减小。
5.contiguity_edges_only—只有共用边界或重叠的相邻面要素会影响目标面要素的计算。
6.contiguity_edges_corners—共享边界、结点或重叠的面要素会影响目标面要素的计算。
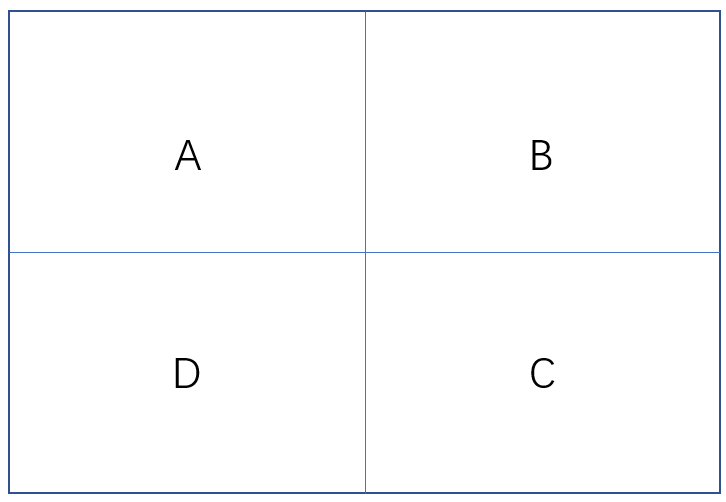
下图，我要研究A区域受哪些区域影响，假如我选取了only，那么B和D与A是有共用边的，而C没有共边，所以C是没影响的。假如我选择corners，那么BCD都有影响，因为他们共享了角。在GeoDa里有Rook和Queen邻接，对应的就是only与corners。一般用这个Queen邻接。
【距离法】
指定计算每个要素与邻近要素之间的距离的方式。有两种。
1.欧氏距离—两点间的直线距离，一般是用这个。
2.曼哈顿距离—沿垂直轴度量的两点间的距离（城市街区）；计算方法是对两点的 x 和 y 坐标的差值（绝对值）求和。
【示例练习】
数据来源：来自全球变化科学研究出版系统“广州都市区118 个街道社会空间质量质量得分”，出自论文“广州市社会空间质量的综合评价与分布格局”......
ArcGIS里计算莫兰指数的工具是【空间统计工具】-【空间自相关】，具体操作步骤都是前面说的几个参数的选择（
记得勾选生成报表文件哦）下图为生成的报表文件。图中已标明此数据是集聚分布的，Moran's I为0.53，p值为0且小于0.01，z得分为9.9远大于2.58，说明有99%的把握认为此数据不是随机分布的，随机分布的可能性小于1%
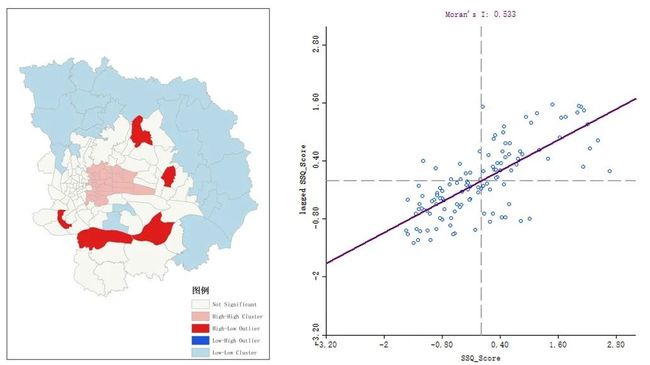
接着来看LISA图...就是局部莫兰指数，在ArcGIS是【聚类和异常值分析】工具，结果显示了具体地区与邻近地区的关系（左图）。
当然也可以用Geoda做空间自相关，还可以顺便出一下莫兰散点图（右图），这四个象限从左上顺时针开始依次代表低高，高高，高低，低低聚集。从数量上来看低低和高高型聚集的街道较高低和低高型的更多，即社会空间质量得分高(低)的街道在空间上更易聚集。
最后还有冷热点分析，可见高值聚类和低值聚类的空间分布格局。
如想用此数据请前往全球变化科学研究出版系统网站自行下载
最后再附一下Geoda下载地址吧
http://geodacenter.github.io/download_windows.html
END
如果在实验过程中有什么地方遇到问题可以后台留言，竭力解答，大概率不会。需要练习数据也请后台留言。如果可以的话，希望能够点个关注转发和分享，点个在看并且点个赞~~
一点规划 求关注/(ㄒoㄒ)/~~
