TeaPearce/Conditional_Diffusion_MNIST 源码阅读

tqdm

 dataset = MNIST("./data", train=True, download=True, transform=tf)
    dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=5)

 for ep in range(n_epoch):
 	...
 	pbar = tqdm(dataloader)
    loss_ema = None
    for x, c in pbar:
    	...

这里的使用了tqdm类库，可参考tqdm类库

超参数预运算

调用了ddpm_schedules来提前计算一些常数值，比如${\beta }_t$、${\sqrt{\alpha }}_t$、$\sqrt{\overline{{\alpha }_t}}$等等，都在返回值的注释中写明了公式。它们都是会用在论文公式中的常数，所以可以提前计算。

def ddpm_schedules(beta1, beta2, T):
    """
    Returns pre-computed schedules for DDPM sampling, training process.
    预计算关于$beta_t$的各种参数，比如sqrt(1-beta_t)等等。它们都是从超参数beta计算而来的常数。
    """
    assert beta1 < beta2 < 1.0, "beta1 and beta2 must be in (0, 1)"

    # 每个t时刻的beta，维度为[T+1]，从beta1递增到beta2
    beta_t = (beta2 - beta1) * torch.arange(0, T + 1, dtype=torch.float32) / T + beta1
    sqrt_beta_t = torch.sqrt(beta_t)
    alpha_t = 1 - beta_t
    log_alpha_t = torch.log(alpha_t)
    alphabar_t = torch.cumsum(log_alpha_t, dim=0).exp()

    sqrtab = torch.sqrt(alphabar_t)
    oneover_sqrta = 1 / torch.sqrt(alpha_t)

    sqrtmab = torch.sqrt(1 - alphabar_t)
    mab_over_sqrtmab_inv = (1 - alpha_t) / sqrtmab

    return {
        "alpha_t": alpha_t,  # \alpha_t
        "oneover_sqrta": oneover_sqrta,  # 1/\sqrt{\alpha_t}
        "sqrt_beta_t": sqrt_beta_t,  # \sqrt{\beta_t}
        "alphabar_t": alphabar_t,  # \bar{\alpha_t}
        "sqrtab": sqrtab,  # \sqrt{\bar{\alpha_t}}
        "sqrtmab": sqrtmab,  # \sqrt{1-\bar{\alpha_t}}
        "mab_over_sqrtmab": mab_over_sqrtmab_inv,  # (1-\alpha_t)/\sqrt{1-\bar{\alpha_t}}
    }

nn.Module.register_buffer

class DDPM(nn.Module):
    # betas: 噪音权重beta的变化幅度，论文设置从0.0001到0.02。beta会随着t逐渐增大，从而令前向传播时，高斯噪声的权重更大。
    def __init__(self, nn_model, betas, n_T, device, drop_prob=0.1):
        super(DDPM, self).__init__()
        self.nn_model = nn_model.to(device)

        # register_buffer allows accessing dictionary produced by ddpm_schedules
        # e.g. can access self.sqrtab later
        for k, v in ddpm_schedules(betas[0], betas[1], n_T).items():
            self.register_buffer(k, v)
        ...

在调用ddpm_schedules整理出需要使用的常数后，调用了nn.Module.register_buffer来注册变量，看注释可知:

This is typically used to register a buffer that should not to be considered a model parameter. For example, BatchNorm’s running_mean is not a parameter, but is part of the module’s state. …

这个方法是用来注册一个变量，但不是模型要训练的参数。换句话说，就是用来注册${\beta }_t$这样的常量，它们不会被反向传播影响。那么怎么使用呢？直接像用成员变量一样，调用self.oneover_sqrta、self.mab_over_sqrtmab即可。

x_i = (
		self.oneover_sqrta[i] * (x_i - eps * self.mab_over_sqrtmab[i])
		+ self.sqrt_beta_t[i] * z
)

绘制动画

在原代码中绘制动画gif图时用到了两种接口，plt.subplots和FuncAnimation。

fig, axs = plt.subplots(nrows=int(n_sample/n_classes), ncols=n_classes,sharex=True,sharey=True,figsize=(8,3))
def animate_diff(i, x_gen_store):
     print(f'gif animating frame {i} of {x_gen_store.shape[0]}', end='\r')
     plots = []
     for row in range(int(n_sample/n_classes)):
         for col in range(n_classes):
             axs[row, col].clear()
             axs[row, col].set_xticks([])
             axs[row, col].set_yticks([])
             # plots.append(axs[row, col].imshow(x_gen_store[i,(row*n_classes)+col,0],cmap='gray'))
             plots.append(axs[row, col].imshow(-x_gen_store[i,(row*n_classes)+col,0],cmap='gray',vmin=(-x_gen_store[i]).min(), vmax=(-x_gen_store[i]).max()))
     return plots
 # 传给
 ani = FuncAnimation(fig, animate_diff, fargs=[x_gen_store],  interval=200, blit=False, repeat=True, frames=x_gen_store.shape[0])    
 ani.save(save_dir + f"gif_ep{ep}_w{w}.gif", dpi=100, writer=PillowWriter(fps=5))
 print('saved image at ' + save_dir + f"gif_ep{ep}_w{w}.gif")

这里的各种调用subplots、animate_diff、FuncAnimation是什么？阅读理解subplots, ax.imshow, FuncAnimation可以帮助深入理解这些调用。

ddpm

接下来看到ddpm网络的核心实现。其forward代表扩散过程，而sample代表还原过程。

forward

    def forward(self, x, c):
        """
        this method is used in training, so samples t and noise randomly
        """

        _ts = torch.randint(1, self.n_T, (x.shape[0],)).to(self.device)  # t ~ Uniform(0, n_T)
        noise = torch.randn_like(x)  # eps ~ N(0, 1)loss

        x_t = (
            self.sqrtab[_ts, None, None, None] * x
            + self.sqrtmab[_ts, None, None, None] * noise
        )  # This is the x_t, which is sqrt(alphabar) x_0 + sqrt(1-alphabar) * eps
        # We should predict the "error term" from this x_t. Loss is what we return.

        # dropout context with some probability
        context_mask = torch.bernoulli(torch.zeros_like(c)+self.drop_prob).to(self.device)
        
        # return MSE between added noise, and our predicted noise
        return self.loss_mse(noise, self.nn_model(x_t, c, _ts / self.n_T, context_mask))

_ts 的意思是采样的时刻t。这里torch.randint的3个参数分别是low, high, shape。也就是说，我们要从[1, T]中采样batch_size个t，然后计算$x_t$。换句话说，输入模型的有batch_size张图片，对于每张图片，我们随机取一个t，让模型预测该时刻下的噪声，再作反向传播。
noise是高斯分布中采样的噪声，维度与图片完全一致。
如何理解 self.sqrtab[_ts, None, None, None]？阅读Pytorch中[:,None]的用法解析可知，[None]可以用于拓展维度，比如以下代码：

res = torch.randn((3,4))
print(res.shape)  // torch.Size([3, 4])
res = res[:,:,None]
print(res.shape)  // torch.Size([3, 4, 1])

这里的变量x_t是论文里t时刻的$x_t$，维度拓展成了[batch_size, 1, 1, 1]。

# 输出为torch.Size([256, 1, 1, 1])
print(self.sqrtab[_ts, None, None, None].shape)

变量x_t的运算过程与原文公式一致：
$$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{\bar{z}}_t$$

context_mask是标签语义掩码。正常情况下，我们希望U-net在预测噪声时，能结合标签再预测。但这里模型希望在输入U-net时，以drop_prob的概率丢弃标签。伯努利分布是一种0-1分布，有p概率采样得到1，1-p概率采样得到0。torch.zeros_like(c)的维度是[batch_size]，也就是说每个批次有一个0或1的值，代表标签是否被掩盖。

self.nn_model(x_t, c, _ts / self.n_T, context_mask)这行代码表示，输入U-net的参数有混噪音的图像$x_t$，标签语义$c$，_ts / self.n_T代表当前时刻t的进度百分比(相较于T)，context_mask代表该样例的标签是否要掩盖。

U-net噪声预测模型

时间刻度t和标签c的信息是如何与图像信息融合，从而指导U-net预测像素点的噪声呢？回顾U-net的结构如下图。

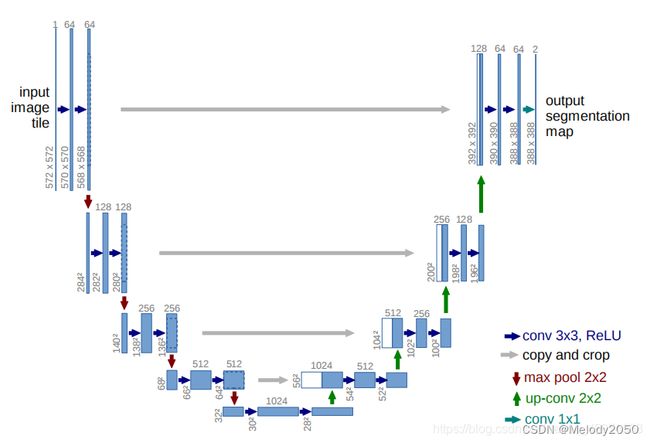
在下采样阶段，卷积层会将输入逐渐降到比较低维度后，进入上采样阶段，隐式向量逐步恢复到原图尺寸大小。而在恢复阶段，下采样阶段的中间向量会与上采样的向量融合，从而指导后者生成更好的结果。
而看向forward代码，其U-net实现是：

1. 为每个时间进度t/T、标签c设置嵌入向量。
2. 与传统U-net不同，上采样阶段用于指导的向量是下采样阶段的中间结果，而在本文还使用了时间向量、标签向量。

def forward(self, x, c, t, context_mask):
    # x is (noisy) image, c is context label, t is timestep, 
    # context_mask says which samples to block the context on

    x = self.init_conv(x)
    down1 = self.down1(x)
    down2 = self.down2(down1)
    hiddenvec = self.to_vec(down2)

    # convert context to one hot embedding
    c = nn.functional.one_hot(c, num_classes=self.n_classes).type(torch.float)
    
    # mask out context if context_mask == 1
    context_mask = context_mask[:, None]
    context_mask = context_mask.repeat(1,self.n_classes)
    context_mask = (-1*(1-context_mask)) # need to flip 0 <-> 1
    c = c * context_mask
    
    # embed context, time step
    cemb1 = self.contextembed1(c).view(-1, self.n_feat * 2, 1, 1)
    temb1 = self.timeembed1(t).view(-1, self.n_feat * 2, 1, 1)
    cemb2 = self.contextembed2(c).view(-1, self.n_feat, 1, 1)
    temb2 = self.timeembed2(t).view(-1, self.n_feat, 1, 1)

    # could concatenate the context embedding here instead of adaGN
    # hiddenvec = torch.cat((hiddenvec, temb1, cemb1), 1)

    up1 = self.up0(hiddenvec)
    # up2 = self.up1(up1, down2) # if want to avoid add and multiply embeddings
    up2 = self.up1(cemb1*up1+ temb1, down2)  # add and multiply embeddings
    up3 = self.up2(cemb2*up2+ temb2, down1)
    out = self.out(torch.cat((up3, x), 1))
    return out

信息向量

U-net为每个时间进度t/T、标签c设置嵌入向量。

首先，定义了嵌入全连接层，用于将输入维度的向量通过全连接层转化到输出维度的向量。

class EmbedFC(nn.Module):
    def __init__(self, input_dim, emb_dim):
        super(EmbedFC, self).__init__()
        '''
        generic one layer FC NN for embedding things  
        '''
        self.input_dim = input_dim
        layers = [
            nn.Linear(input_dim, emb_dim),
            nn.GELU(),
            nn.Linear(emb_dim, emb_dim),
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x):
        x = x.view(-1, self.input_dim)
        return self.model(x)

时间进度是个一维向量，取值范围在[0, 1]，可用线性层转化为高维向量。比如这里的timeembed1会将1维向量转化到2*n_feat维度。

self.timeembed1 = EmbedFC(1, 2*n_feat)
...
temb1 = self.timeembed1(t).view(-1, self.n_feat * 2, 1, 1)
..

同理，标签c可视为长度为n_classes的one-hot向量，通过线性层contextembed1转化为2*n_feat的长度(最后view函数再拓展到4维)

self.contextembed1 = EmbedFC(n_classes, 2*n_feat)
cemb1 = self.contextembed1(c).view(-1, self.n_feat * 2, 1, 1)

语义向量的长度以n_feat为基准，可以是n_feat、2*n_feat

掩码向量conext_mask

下列代码可以使掩码向量发生作用，当标签向量要被遮盖时，其乘法结果为0，否则不变。

# mask out context if context_mask == 1
context_mask = context_mask[:, None]
context_mask = context_mask.repeat(1,self.n_classes)
context_mask = (-1*(1-context_mask)) # need to flip 0 <-> 1
c = c * context_mask

上采样层的信息融合

那么上采样层是如何将各种信息向量融合的呢？首先，U-net的上采样层定义为UnetUp，其接收x, skip两个参数，将它们拼接后交给逆卷积层。

class UnetUp(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(UnetUp, self).__init__()
        '''
        process and upscale the image feature maps
        '''
        layers = [
            nn.ConvTranspose2d(in_channels, out_channels, 2, 2),
            ResidualConvBlock(out_channels, out_channels),
            ResidualConvBlock(out_channels, out_channels),
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x, skip):
        # 关键行为
        x = torch.cat((x, skip), 1)
        x = self.model(x)
        return x
      
class ContextUnet(nn.Module):
    def __init__(self, in_channels, n_feat = 256, n_classes=10):
    	...
		self.up1 = UnetUp(4 * n_feat, n_feat)

那么上采样阶段的信息融合代码如下，可见，在一个上采样步骤

• cemb1*up1+ temb1先将信息向量与up1相乘，再将其加上时间向量temb1。
• 然后，混合向量与down2一同输入上采样层，其实做了拼接操作。

up1 = self.up0(hiddenvec)
up2 = self.up1(cemb1*up1+ temb1, down2)  # add and multiply embeddings
up3 = self.up2(cemb2*up2+ temb2, down1)
out = self.out(torch.cat((up3, x), 1))

用先乘法，再加法的方式融合时间和标签两种信息向量是否合理？

恢复阶段

sample函数展示了恢复阶段，其对应了图中红框部分的功能。

模型使用了双批次生成的做法，将输入复制为两批，第一批禁用标签向量作指导，第二批则使用标签向量作指导。之后，在每个还原步骤的时刻t，按照权重guide_w将两种中间结果混合。

Q：如何禁用标签？
A：利用上文分析过的context_mask机制，将上半批的掩码设置为0，下半批的掩码设置为1即可。

# don't drop context at test time
context_mask = torch.zeros_like(c_i).to(device)

# double the batch
c_i = c_i.repeat(2)
context_mask = context_mask.repeat(2)
context_mask[n_sample:] = 1. # makes second half of batch context free

Q：guide_w是如何如何混合两种中间结果？
A：参考代码，

 # split predictions and compute weighting
eps = self.nn_model(x_i, c_i, t_is, context_mask)
eps1 = eps[:n_sample]
eps2 = eps[n_sample:]
eps = (1+guide_w)*eps1 - guide_w*eps2

可知，(1+guide_w)*eps1 - guide_w*eps2是混合的计算公式。本人还不太理解这种做法，为什么要以无标签的噪声减去有标签的噪声，而不是两者相加。

然后，代码中x_i遵从论文迭代公式。

z = torch.randn(n_sample, *size).to(device) if i > 1 else 0
x_i = (
  self.oneover_sqrta[i] * (x_i - eps * self.mab_over_sqrtmab[i])
    + self.sqrt_beta_t[i] * z
)

这是一个从高斯分布采样，z采样自标准高斯分布，前半部分是均值，后半部分是方差。

前半部分是均值，显然遵从下方公式
$${\tilde{\mathbf{\mu }}}_t=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{a}}_t}}{ϵ}_t\right)$$
后半部分是方差，应该使用了简化版本的${\sqrt{\beta }}_t$。

应该没有遵从如下公式：
$$\frac{1}{{\sigma }^2}=\frac{1}{{\tilde{\beta }}_t}=\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right);{\tilde{\beta }}_t=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t$$

总结

这份代码实现了diffusion的骨架，并用到了如下技巧：

1. 上下文信息掩码context_mask与双输入混合生成guide_w的技巧。
2. 使用乘法和加法，将上下文信息、时间刻度信息混入向量，指导U-net预测噪音的技巧。但语义向量的融合方式或许还能改进
3. tqdm进度条的使用、matplotlib动画的生成。

后记

自失业以后已经几个月了，学习这些不知道能有何用，但只是凭着兴趣在学。