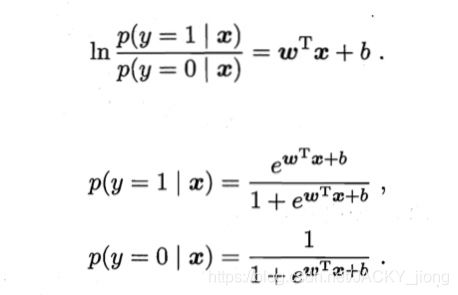机器学习算法(一): 基于逻辑回归的分类预测
机器学习算法(一): 基于逻辑回归的分类预测
- 了解 逻辑回归 的理论
-
- 线性模型的基本概念
- 公式推导
- 公式变形
- 对数几率回归(逻辑回归)
-
- 公式导出
- 公式应用
- 掌握 逻辑回归 的 sklearn 函数调用使用并将其运用到鸢尾花数据集预测
-
- STEP1(函数库导入)
- STEP2(数据读取/载入)
- STEP3(数据信息简单查看)
- STEP4(数据可视化)
-
- 2D可视
-
- *pairplot*
- *箱型图*
- 3D
- STEP5(利用 逻辑回归模型 在二分类上 进行训练和预测)
-
- 二分类
- (利用 逻辑回归模型 在三分类(多分类)上 进行训练和预测)
了解 逻辑回归 的理论
线性模型的基本概念
在日常生活中,我们对于某一件事情的判断往往是一个二分类问题,二分类顾名思义就是将情况分为两类:
如这个西瓜是好瓜还是坏瓜,这只猫可爱不可爱,等下会下雨还是不下雨……
这些问题都需要我们做出判断,我们往往用Y来表示我们的判断,因为二分类问题,所以通常用[-1,1]或者[0,1]来标记我们的最终判断,而支撑我们做出判断的条件,即该事物的特征,如瓜的纹理,大小,有无藤;猫的品种,大小,年纪;此时的云层密度,空气湿度;我们将做这些作为支撑我们做出判断的特征用X来表示,通常x有很多个特征组成(比如,只看西瓜的大小的难以判断西瓜好不好),我们用 x 1 , x 2 . . . . x n x_1,x_2....x_n x1,x2....xn来表示,而且每个特征对于我们做成判断的影响程度即权重不同,所以我们又引入了 ω标记每个特征的权重, ω 1 , ω 2 . . . . ω n ω_1,ω_2....ω_n ω1,ω2....ωn与 x 1 , x 2 . . . . x n x_1,x_2....x_n x1,x2....xn一一对应。
所以在了解基本概念以及每个符号所代表的含义以后,我们要做的就是建立线性模型。
公式推导
f ( x ) = ω T x + b f(x)=\omega^T x+b f(x)=ωTx+b
- f(x)为通过公式计算出的模型预测结果
- x为特征值
- ω \omega ω为每个特征值的权重
- y为实际的结果
PS:f(x)可以理解为电脑做出的判断,可能会错的(我们的目的就是让他尽可能对,逼近人脑的正确率);y为人脑做出的判断,是塑造模型前就已经有了的,是100%正确的。
目标: f ( x i ) = ω x i + b , 使 得 f ( x i ) ≈ y i f(x_i)=\omega x_i+b,使得f(x_i)\approx y_i f(xi)=ωxi+b,使得f(xi)≈yi
方法(最小化均方误差):
( ω ∗ , b ∗ ) = a r g m i n ( ω , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 (\omega ^*,b^*)=argmin_(\omega,b) \sum_{i=1}^{m}(f(x_i)-y_i)^2 (ω∗,b∗)=argmin(ω,b)i=1∑m(f(xi)−yi)2
= a r g m i n ( ω , b ) ∑ i = 1 m ( y i − ω x i − b ) 2 =argmin_(\omega,b) \sum_{i=1}^{m}(y_i-\omega x_i-b)^2 =argmin(ω,b)i=1∑m(yi−ωxi−b)2
我们可以将 ∑ i = 1 m ( f ( x i ) − y i ) 2 \sum_{i=1}^{m}(f(x_i)-y_i)^2 ∑i=1m(f(xi)−yi)2理解为错误的量化累加,累计越大说明这个模型越垃圾,测得越不准,累计越小说明这个模型越牛掰,测得越准。
至于如何最小化均方误差,这里运用到了“最小二乘法”,其数学原理在此不做解释,我们只需要知道将 E ( ω , b ) 对 ω 和 b E_(\omega,b)对\omega 和b E(ω,b)对ω和b分别求导且取零解出 ω , b \omega,b ω,b就是我们最终模型所要的答案。
公式过程如下:
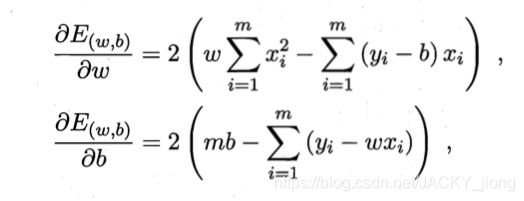
以上两条公式各自取零即可得到以下的解:
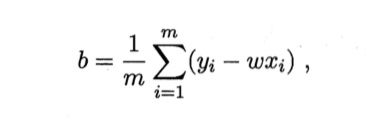
读到这里你可能已经发现,以上的线性模型这是应用于单特征值的预测,但是实际上多个特征值的预测与它殊途同归——“多元线性回归”:
f ( x i ) = ω T x i + b , 使 得 f ( x i ) ≈ y i f(x_i)=\omega^Tx_i+b,使得f(x_i)\approx y_i f(xi)=ωTxi+b,使得f(xi)≈yi
关于最优解的求解与单特征值的求解方法相同,但由于矩阵的存在需要简单的讨论。这里不做推导(推导也是复制黏贴,看官可以去别的大佬那里看就行了,嘻嘻)。
公式变形
通过以上的公式推导,我们已经了解并得到了线性回归模型及其公式表达,为了便于观察,我们把线性回归模型简写为 y = ω T x + b y=\omega^Tx+b y=ωTx+b
但有时我们的线性模型可能不能直接估测y的大小,而需要通过一个y的直接函数来间接表达预测,为什么这样绕弯下文揭晓!
这里便引入了“对数线性回归” l n y = ω T x + b lny=\omega^Tx+b lny=ωTx+b
虽然y,x在函数空间上无法一一直接对应,但x,y仍然还是线性关系。
更一般地,考虑到单调可微函数g(·),令
y = g − 1 ( ω T x + b ) ( 广 义 线 性 模 型 ) y=g^{-1}(\omega^Tx+b) (广义线性模型) y=g−1(ωTx+b)(广义线性模型)
对数几率回归(逻辑回归)
公式导出
学到这里,或许有人会有疑惑了,明明是一开始我们都在讨论二分类问题,判断是好瓜还是坏瓜,怎么用的公式都是回归公式,通过回归公式算出的必然是一个连续的值,y又怎么会是一开始设定的[-1,1]或[0,1]
我们以[0,1]为例,如何将公式输出的值与0,1联系起来成为了分类的关键。我们可以这么想,对于人群年龄的定位是一个分类问题,为了简化描述,我们就分两类人:老人,年轻人。而我们通常是用年龄来区分他们的,这也是最直接准确的方法。最简单的划分方法也就是通过年龄一刀切。设定一个阈值,超过这个值的都是老人,低于就是年轻人。这里的老人(设为1),年轻人(设为0)就是我们最终想要的y,而年龄就是线性回归模型预测的值,我们用z来表示。为了z–>y的转化,这里便用到了阶跃函数,我们可以想象阶跃函数的图像,当x>=0是,y=1;x<0,y=0;这就能很好的还原阈值的概念。即
y = w ( z ) y=w(z) y=w(z)
这与上文的广义线性模型其实就是一个东西。
但是阶跃函数是一个理想模型,且不连续,我们没办法找到一个函数完全符合他,所以我们需要用找到一个一定程度上近似单位阶跃函数的替代函数,并希望它单调可微,所以天降猛男“对数几率函数”横空出世:
y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1
即 y = 1 1 + e − ω T x + b y=\frac{1}{1+e^{-\omega^Tx+b}} y=1+e−ωTx+b1
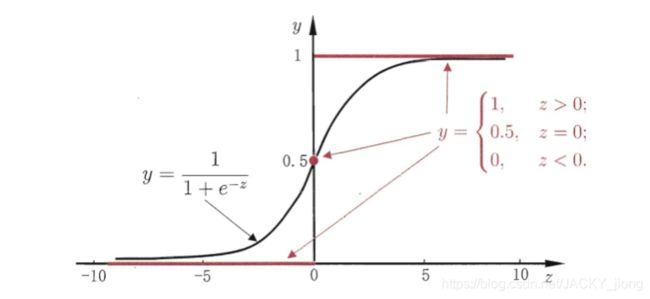
从而推出
l n y 1 − y = ω T x + b ln{\frac{y}{1-y}}=\omega^Tx+b ln1−yy=ωTx+b
在这我们将y视为x作为正例的可能性,那么1-y自然就是其反例可能性。两者相比取ln,这便是对数几率函数的由来。
公式应用
掌握 逻辑回归 的 sklearn 函数调用使用并将其运用到鸢尾花数据集预测
逻辑回归的实战演练以鸢尾花的种类判断为例(山鸢尾 (Iris-setosa),变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)),根据四种特征预测种类,分别是:
花萼长度(cm)----sepal length
花萼宽度(cm)----sepal width
花瓣长度(cm)----petal length
花瓣宽度(cm)----petal width
鸢尾的三个亚属类别,‘setosa’(0), ‘versicolor’(1), ‘virginica’(2)----target
STEP1(函数库导入)
## 基础函数库
import numpy as np
import pandas as pd
## 绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns
STEP2(数据读取/载入)
##我们利用sklearn中自带的iris数据作为数据载入,并利用Pandas转化为DataFrame格式
from sklearn.datasets import load_iris
data = load_iris() #得到数据特征
iris_target = data.target #得到数据对应的标签
iris_features = pd.DataFrame(data=data.data,columns=data.feature_names) #利用Pandas转化为DataFrame格式
鸢尾花的数据集在sklearn中就有,直接调用即可,不用手动输入。
STEP3(数据信息简单查看)
##利用.info()查看数据的整体信息
iris_features.info()
##STEP4(数据可视化)
## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝,防止对于原始数据的修改
iris_all['target'] = iris_target
2D可视
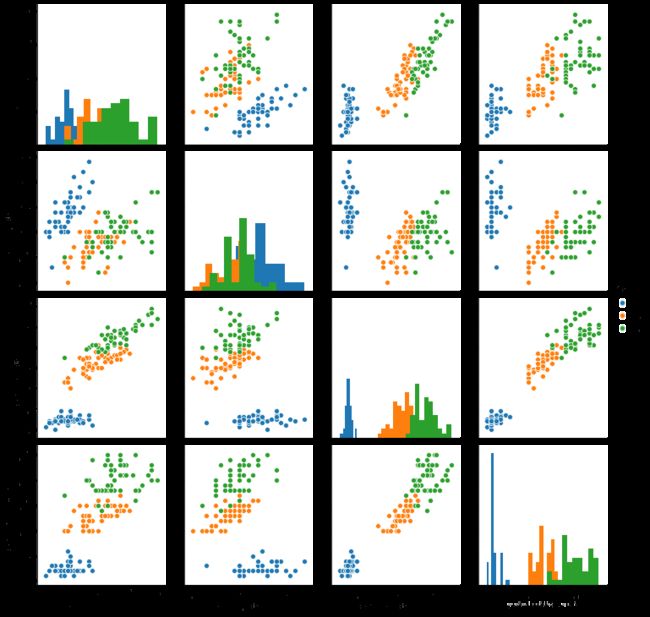
pairplot
## 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()
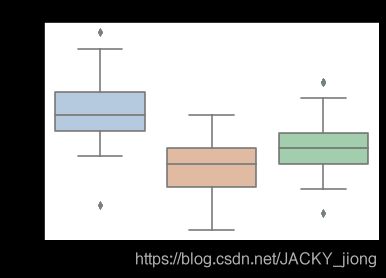
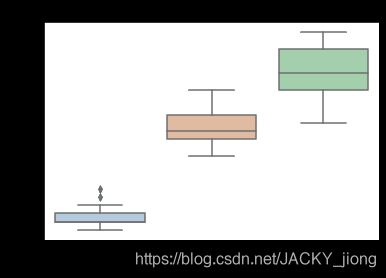
箱型图
for col in iris_features.columns:
sns.boxplot(x='target', y=col, saturation=0.5,
palette='pastel', data=iris_all)
plt.title(col)
plt.show()
3D
# 选取其前三个特征绘制三维散点图
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')
iris_all_class0 = iris_all[iris_all['target']==0].values
iris_all_class1 = iris_all[iris_all['target']==1].values
iris_all_class2 = iris_all[iris_all['target']==2].values
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()
plt.show()
STEP5(利用 逻辑回归模型 在二分类上 进行训练和预测)
二分类
##为了正确评估模型性能,将数据划分为训练集和测试集,并在训练集上训练模型,在测试集上验证模型性能。
from sklearn.model_selection import train_test_split
##选择其类别为0和1的样本(不包括类别为2的样本)
iris_features_part=iris_features.iloc[:100]
iris_target_part=iris_target[:100]
#df.iloc[:100]取前100行
##测试集大小为20%,80%/20%分
x_train,x_test,y_train,y_test=train_test_split(iris_features_part,iris_target_part,test_size=0.2,random_state=2020)
先只进行二分类,所以只取前100个数据集,0-49是样本1,50-99是样本2。
##从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
##定义逻辑回归模型
clf=LogisticRegression(random_state=0,solver='lbfgs')
##在训练集上训练逻辑回归模型
clf.fit(x_train,y_train)
##查看其对应的w
print('the weight of Logistic Regression:',clf.coef_)
##查看其对应的w0
print('the intercept(w0) of Logistic Regression:',clf.intercept_)
##在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(x_train)
test_predict=clf.predict(x_test)
from sklearn import metrics
##利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
##查看混淆矩阵(预测值和真实值的各类情况统计矩阵)
confusion_matrix_result=metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
##利用热力图对于结果进行可视化
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_result,annot=True,cmap='Blues')
plt.xlabel('Predictedlabels')
plt.ylabel('Truelabels')
plt.show()
##The accuracy of the Logistic Regressionis:1.0
##The accuracy of the Logistic Regressionis:1.0
##The confusion matrix result:
##[[9 0]
##[0 11]]
(利用 逻辑回归模型 在三分类(多分类)上 进行训练和预测)
##测试集大小为20%,80%/20%分
x_train,x_test,y_train,y_test=train_test_split(iris_features,iris_target,test_size=0.2,random_state=2020)
##定义逻辑回归模型
clf=LogisticRegression(random_state=0,solver='lbfgs')
##在训练集上训练逻辑回归模型
clf.fit(x_train,y_train)
##查看其对应的w
print('the weight of Logistic Regression:\n',clf.coef_)
##查看其对应的w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
##由于这个是3分类,所有我们这里得到了三个逻辑回归模型的参数,其三个逻辑回归组合起来即可实现三分类
##在训练集和测试集上分布利用训练好的模型进行预测
train_predict=clf.predict(x_train)
test_predict=clf.predict(x_test)
##由于逻辑回归模型是概率预测模型(前文介绍的p=p(y=1|x,\theta)),所有我们可以利用predict_proba函数预测其概率
train_predict_proba=clf.predict_proba(x_train)
test_predict_proba=clf.predict_proba(x_test)
print('The test predict Probability of each class:\n',test_predict_proba)
##其中第一列代表预测为0类的概率,第二列代表预测为1类的概率,第三列代表预测为2类的概率。
##利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
##查看混淆矩阵
confusion_matrix_result=metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
##利用热力图对于结果进行可视化
plt.figure(figsize=(8,6))
sns.heatmap(confusion_matrix_result,annot=True,cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
##The confusion matrix result:
##[[10 0 0]
##[0 8 2]
##[0 2 8]]
以上仅为个人学习笔记,如有错误还请指出。
参考资料:《机器学习》周志华