使用Python实现单隐藏层神经网络的训练

1 实验内容

不使用Keras，Tensorfolow 或Pytorch 等框架，仅使用Numpy，Scipy 和Matplotlib 等Python 常用科学计算库，完成单隐藏层的全连接神经网络（和之后要讲的卷积神经网络形成对比），实现Scikit-learn 里的half moons 数据集的分类。

2 实验要求

• 使用Scikit-learn 加载half moon 数据，实现数据的可视化
• 构建单隐藏层的全连接神经网络，参考课件的内容，推导正、反向传播并给出代码实现
• 考虑不同的激活函数、不同的隐藏层宽度对网络训练和性能的影响
• 需要具备的功能或者模块：数据读取、加载，正反向传播，使用梯度下降训练模型（可采用mini-batch 的随机梯度下降方法），模型训练、测试性能指标的显示和评估
• PPT 汇报（每组3min），提交2-4 页实验报告，需简要叙述方法原理、实验步骤、方法参数讨论、实验结果；需明确说明组员分工、给出组内排名（可标注同等贡献#）。

3 实验原理

多层感知机：

多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network），除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构，如下图：

前向传播与后向传播

神经网络实际上就是一个输入为输出为的映射函数:,只要我们通过训练得到较优的参数,那么对于任何输入我们都能得到一个与之对应的输出,至于是不是正确的,误差有多大,那就是效果的问题了。

**前向传播( Forward propagation)与反向传播( Back propagation)**是神经网络中的两个基础概念,其实模拟的就是人脑中神经元的正向传导和反向反馈信号回路。

这是一场以误差 Error为主导的反向传播 Back Propagation运动,目的是得到最优的全局参数矩阵：

前向传播输入信号直至输出产生误差,反向传播误差更新重矩阵

这句话很好地形容了信息的流动方向,权重得以在信息双向流动中得到优化,可以理解为一个带反馈校正循环的电子信号处理系统。

我们可以使用梯度下降法去优化误差。如果没有隐藏层,那么输岀层接受输入层传递的数据并产生结果,通过计算产生的误差,可以直接将误差反馈给输出层,知道参数向更优的方向调整。也就是说,此时,可以直接通过误差进行参数优化。

但是如果加入隐藏层，误差可以被直接反馈给输出层，即直接通过误差进行参数优化;然而隐藏层则不能得到误差反馈，即不能够被直接优化。反向传播算法使得误差可以被传递到隐藏层，进而产生间接误差,则隐藏层左侧的权重矩阵可以通过间接误差得到权重更新，进行迭代优化。

4 具体实现

数据加载与可视化：

从make_moons函数来生成数据集，并划分训练集与测试集。

X, y = datasets.make_moons(num, noise=0.2) #产生数据集

train_X, train_y = np.array(X[:train_num]), np.array(y[:train_num])
test_X, test_y = np.array(X[train_num:]), np.array(y[train_num:])

对数据进行可视化。

def draw(X, y, name='yuanshi.png'):
    plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)
    plt.savefig(name)

激活函数：

我们选取了几种经典的激活函数进行实现。

有使用很多的ReLU，Sigmoid，Tanh：

class ReLU:
    def __init__(self):
        self.mask = None
        self.out = None
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        self.out = out
        return out
    def backward(self):
        dx = self.out
        return dx
class Sigmoid:
    def __init__(self):
        self.out = None
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out
    def backward(self):
        dx = (1.0 - self.out) * self.out
        return dx
class Tanh:
    def __init__(self):
        self.out = None
    def forward(self, x):
        out = (1 - np.exp(-2 * x)) / (1 + np.exp(-2 * x))
        self.out = out
        return out
    def backward(self):
        dx = 1 - np.power(self.out, 2)
        return dx
    

也有对ReLU的后续改进，LeakyReLU、ELU、SELU。

SELU部分参考https://github.com/bioinf-jku/SNNs/blob/master/SelfNormalizingNetworks_MLP_MNIST.ipynb

class LeakyRelu:
    def __init__(self,alpha):
        self.out, self.alpha = None, alpha
    def forward(self, x):
        mask = (x <= 0)
        out = x.copy()
        out[mask] = x[mask] * self.alpha
        self.out = out
        return out
    def backward(self):
        dx = np.where(self.out>=0, 1, self.alpha)
        return dx

class ELU:
    def __init__(self, alpha=0.1):
        self.alpha = alpha
        self.x = None
        self.out = None

    def forward(self, x):
        self.x = x 
        self.out = np.where(x >= 0.0, x, self.alpha * (np.exp(x) - 1))
        return self.out

    def backward(self):
        return np.where(self.x >= 0.0, 1, self.out + self.alpha)

class SELU:
    def __init__(self):
        self.alpha = 1.6732632423543772848170429916717
        self.scale = 1.0507009873554804934193349852946 
		self.x = None
		self.out = None
        
    def forward(self, x):
        self.x = x 
        self.out = self.scale * np.where(x >= 0.0, x, self.alpha*(np.exp(x)-1))
        return self.out

    def backward(self):
        return self.scale * np.where(self.x >= 0.0, 1, self.alpha * np.exp(x))

单隐层神经网络

这里搭建了一个单隐层的神经网络。

class bpNN:
    def __init__(self, input_dim, numH, numO, learning_rate, reg_lambda, grad = 'tanh'):
        self.numH = numH
        self.numO = numO
        self.learning_rate = learning_rate
        self.reg_lambda = reg_lambda
        #初始化权重和偏置
        self.weight_H = np.random.random([input_dim, self.numH]) * 0.001
        self.b_H = np.zeros([1,self.numH])
        self.weight_O = np.random.random([self.numH, self.numO]) * 0.001
        self.b_O = np.zeros([1,self.numO])
        self.AF = None
        if grad == 'sigmoid':
            self.AF = Sigmoid()
        elif grad == 'tanh':
            self.AF = Tanh()
        elif grad == 'relu':
            self.AF = ReLU()
        elif grad == 'leakyrelu':
            self.AF = LeakyReLU()
        elif grad == 'ELU':
            self.AF = ELU()
        elif grad == 'SELU':
            self.AF = SELU()

前向传播

def z_a(self, x): #计算隐层z1 = w1x + b1, a1 = sigmoid(z1), 输出层z2 = w2a1 + b2
    z1 = np.dot(x, self.weight_H) + self.b_H
    a1 = self.AF.forward(z1)
    z2 = np.dot(a1, self.weight_O) + self.b_O
    z = z2 - np.max(z2)
    exp_scores = np.exp(z)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
    return z1, a1, z2, probs

后向传播

通过后向传播更新权重。

def train(self, x, y): #训练函数, BP误差传递主体
    z1, a1, z2, probs = self.z_a(x)
    delta3 = probs - y
    dw2 = np.dot(a1.T, delta3)
    db2 = np.sum(delta3, axis=0, keepdims=True)
    delta2 = np.dot(delta3, self.weight_O.T) * self.AF.backward()
    dw1 = np.dot(x.T, delta2)
    db1 = np.sum(delta2, axis=0)
    # dw2 += self.reg_lambda * self.weight_O
    # dw1 += self.reg_lambda * self.weight_H
    self.weight_H -= self.learning_rate * dw1
    self.b_H -= self.learning_rate * db1
    self.weight_O -= self.learning_rate * dw2
    self.b_O -= self.learning_rate * db2

Mini-batch梯度下降：

for i in range(iter):
    for j in range(0, train_num, batch_size):
        net.train(train_X[j:j+batch_size], make_one_hot(train_y[j:j+batch_size]))

预测与评估：

def predict(self, x): #预测函数
    z1, a1, z2, probs= self.z_a(x)
    return np.argmax(probs,axis=1)

def accuracy(self, x, y):
    predict_y = self.predict(x)
    acc = 1 - np.sum(abs(predict_y-y))/len(y)
    return acc

分类结果可视化：

def draw_p(X, y, net, name='yuanshi1.png'):
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = np.floor(net.predict(np.c_[xx.ravel(), yy.ravel()]) * 1.99999)
    Z = Z.reshape(xx.shape)
    #预测分界图像s
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
    plt.savefig(name)

5 实验结果

不同激活函数：

固定网络结构，只更换激活函数，得到最终模型的acc进行对比。

activation_functions	test-acc
Sigmoid	0.972
Tanh	0.8614999999999999
ReLU	0.965
Leaky-ReLU	0.862
ELU	0.869
SELU	0.8815

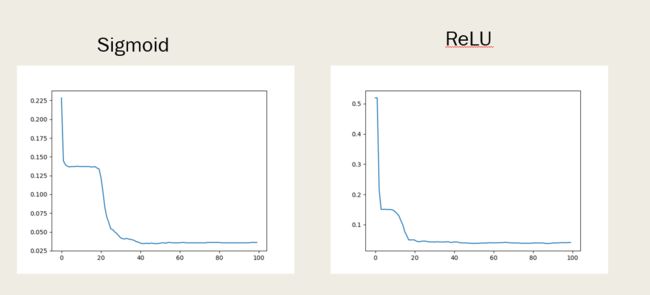
收敛速度

观察到虽然只有一层，但ReLU的收敛速度依然稍快。

分类结果可视化

这里只展示了使用Sigmoid时的分类结果。
]