基于邻接矩阵的有向图的广度优先遍历(BFS)和深度优先遍历(DFS)算法
BFS
概念:广度优先遍历算法是图的另一种基本遍历算法,其基本思想是尽最大程度辐射能够覆盖的节点,并对其进行访问。
以迷宫为例,广度优先搜索则可以想象成一组人一起朝不同的方向走迷宫,当出现新的未走过的路的时候,可以理解成一个人有分身术,继续从不同的方向走,,当相遇的时候则是合二为一,那么也就类似于树的层次遍历,当访问完一层后接下去访问,唯一的区别就是图存在回路,为了避免二次访问需要添加一个访问数组,来判断当前节点是否被访问过。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓下面给出有向图的例子↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
那么根据BFS的思想假设以v1作为起始顶点,依次向下遍历顺序为 V1->V0->V2->V4->V3,如果根据树的层次遍历应用在BFS上,当V0遍历完后将V0的邻接点V1 V4 依次入队 访问v1再重复以上步骤,当队为空时,遍历完成。这里只是用邻接节点代替了左右孩子的思想,本质还是层次遍历
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓下面给出具体代码实现↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
void BFS(PGraph G,int v,bool visited [])
{
//广度优先遍历图,v-->首个要遍历的节点
printf(" %d ",v);
visited[v] = true; //首个节点已访问
Queue Q;
Init_Queue(&Q); //初始化队列
En_Queue(&Q,v); //首个元素入队
while(!is_Empty(&Q)) //队列非空
{
int ver = out_Queue(&Q); //获取首个节点
for(int w = firstArc(G,ver);w>=0;w=adjArc(G,ver,w))
{ // firstArc()->根据给定顶点返回第一个相邻的边的依附节点
//表示ver相对于w的下一个邻接节点
if(!visited[w])
{
printf(" %d ",w);
visited[w] = true;
En_Queue(&Q,w);
}
}
}
}
int firstArc(PGraph G,int ver)
{
//根据给定ver去领接矩阵中找到第一个领接节点
for(int i = 0;ivertexNums;i++)
{
if(G->ArcType[ver][i]==1) //当前j表示的是ver的第一个邻接点
return i; //将j顶点返回
}
return -1;
}
int adjArc(PGraph G,int ver,int w)
{
//返回顶点ver相对于w的下一个邻接点
for(int i = w+1;ivertexNums;i++)
{
if(G->ArcType[ver][i]==1)
{
return i;
}
}
return -1;
} ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 下面是求第一个邻接节点和其余邻接节点的实现代码↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
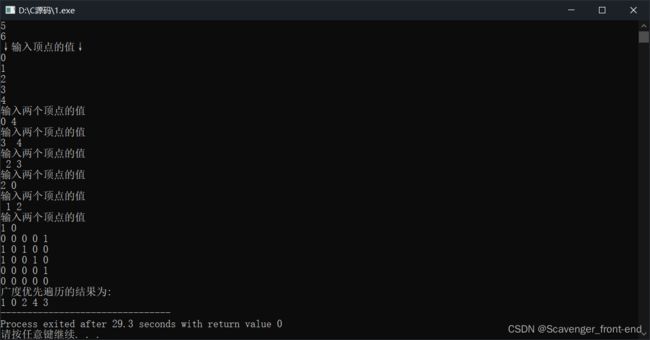
结果如我们所见,这里的1 0 2 4 3分别对应的顶点在顶点表中对应的索引值
DFS
深度优先遍历主要思路是从图中一个未访问的顶点 V 开始,沿着一条路一直走到底,然后从这条路尽头的节点回退到上一个节点,再从另一条路开始走到底…,不断递归重复此过程,直到所有的顶点都遍历完成,它的特点是不撞南墙不回头,先走完一条路,再换一条路继续走。
树是图的一种特例(连通无环的图就是树),接下来我们来看看树用深度优先遍历该怎么遍历。
深度优先遍历同树的递归遍历类似, 当访问到最深层的节点,就返回访问另一分支,只是与树不同的也是会存在回路所以需要传入判断数组来判断当前索引是否被访问过
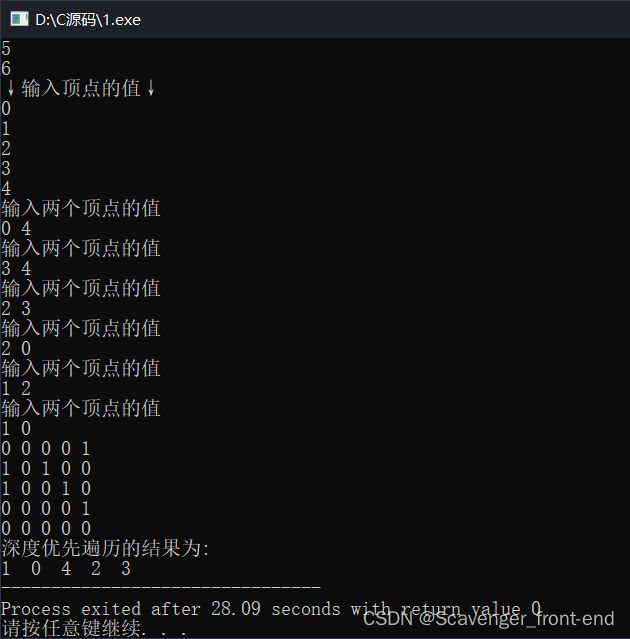
根据上述定理,通过DFS得出的结果就应该为V1->V0->V4->V2->V3
具体代码如下
void DFS(PGraph G,bool visited [],int v) //v->顶点
{
//深度优先遍历查找数组
printf("%d ",v);
visited[v] = true;
for(int j = 0;jvertexNums;j++)
{
if(G->ArcType[v][j]!=0&&!visited[j]) //当I->J 之间有边 并且 j顶点没被访问过
{
DFS(G,visited,j);
}
}
}
全部实现代码如下
#include
#include
#define Maxsize 20
typedef struct Graph{
int vertex[20];//定义顶点表
int ArcType[20][20];
int vertexNums,arcNums; //定义边的和顶点的数量
}Graph,*PGraph;
typedef struct Queue{
int *VerIndex;//顶点的索引
int front,rear;
}Queue,*PQueue;
void Init_Queue(PQueue Q)
{
Q->VerIndex = (int*)malloc(sizeof(int)*Maxsize); //为队列分配一个20内存大小的空间
if(Q->VerIndex == NULL)
{
printf("分配失败 ");
}
Q->front = 0;
Q->rear = Q->front;
}
bool is_Empty(PQueue Q)
{
if(Q->rear == Q->front)
{
return true;
}
return false;
}
void En_Queue(PQueue Q,int index)
{
if((Q->rear+1)%10==Q->front)
{
printf("队列满,无法插入新元素");
}
Q->VerIndex[Q->rear] = index;
Q->rear++;
}
int out_Queue(PQueue Q)
{
if(is_Empty(Q))
{
printf("队列为空");
exit(-1);
}
int index;
index = Q->VerIndex[Q->front];
Q->front++;
return index;
}
int Location(PGraph G,char data)
{
for (int j = 0; j< G->vertexNums; j++)
{
if(G->vertex[j] == data)
{
return j;
}
}
return -1;
}
void Init_Graph(PGraph G)
{
int ver = 0,arc = 0;
printf("定义顶点数和边数\n");
scanf("%d %d",&ver,&arc);
G->arcNums = arc;G->vertexNums = ver;
printf("↓输入顶点的值↓\n");
int temp;
for (int i = 0; i < G->vertexNums; i++)
{
scanf("%d",&temp);
G->vertex[i] = temp;
}
for (int i = 0; i vertexNums ; i++)
{
for (int j = 0; j vertexNums; j++)
{
G->ArcType[i][j] = 0;//将所有标志赋为0 代表当前没有连接
}
}
getchar();
int v1,v2;
int index1,index2;
for (int i = 0; iarcNums;i++)
{
printf("输入两个顶点的值\n");
scanf("%d %d",&v1,&v2);
index1 = Location(G,v1);index2 = Location(G,v2);
//获得两个顶点的索引
G->ArcType[index1][index2] = 1;
}
}
void DFS(PGraph G,bool visited [],int v) //v->顶点
{
//深度优先遍历查找数组
printf("%d ",v);
visited[v] = true;
for(int j = 0;jvertexNums;j++)
{
if(G->ArcType[v][j]!=0&&!visited[j]) //当I->J 之间有边 并且 j顶点没被访问过
{
DFS(G,visited,j);
}
}
}
int firstArc(PGraph G,int ver)
{
//根据给定ver去领接矩阵中找到第一个领接节点
for(int i = 0;ivertexNums;i++)
{
if(G->ArcType[ver][i]==1) //当前j表示的是ver的第一个邻接点
return i; //将j顶点返回
}
return -1;
}
int adjArc(PGraph G,int ver,int w)
{
//返回顶点ver相对于w的下一个邻接点
for(int i = w+1;ivertexNums;i++)
{
if(G->ArcType[ver][i]==1)
{
return i;
}
}
return -1;
}
void BFS(PGraph G,int v,bool visited [])
{
//广度优先遍历图,v-->首个要遍历的节点
printf("%d ",v);
visited[v] = true; //首个节点已访问
Queue Q;
Init_Queue(&Q); //初始化队列
En_Queue(&Q,v); //首个元素入队
while(!is_Empty(&Q)) //队列非空
{
int ver = out_Queue(&Q); //获取首个节点
for(int w = firstArc(G,ver);w>=0;w=adjArc(G,ver,w))
{ // firstArc()->根据给定顶点返回第一个相邻的边的依附节点
//表示ver相对于w的下一个邻接节点
if(!visited[w])
{
printf("%d ",w);
visited[w] = true;
En_Queue(&Q,w);
}
}
}
}
int main(){
Graph G;
Init_Graph(&G);
for (int i = 0; i < G.vertexNums; i++)
{
for (int j = 0; j