Pymoo：基于多准则决策制定 (MCDM) 方法的算法设计

pymoo: 基于 Python 的多目标优化仓库 (MOO, Multi-objective Optimization) : anyoptimization/pymoo Github 仓库地址。

一、多准则决策制定 (MCDM, Multi-Criteria Decision Making)

• Multi-Criteria Decision Making的内涵：
  在多目标优化过程中，我们会获得一组非支配(non-dominated)的解，当有了这些可以做决策的非支配解的时候，我们如何做决策呢？这个问题正是我么为什么要做多目标优化的目的。我们可以根据的最优方案(非支配解)做出单个决定，这个过程就是所谓的多准则决策制定(MCDM)。

虽然，Pymoo的主要重点在于优化，而不是 MCDM，但是该框架同样提供了一些基本的相关工具，可用于MCDM问题的分析，最终寻找一个理论上最优的决策。

二、MCDM相关的基本分析方法

2.1 折中编程 (Compromise Programming)

我们可以使用任何标量化方法，并将其用于后处理（post-processing）。假设我们的算法已经收敛于Pareto前沿，我们可以通过以下几步实现折中编程方法：

说明：
（1）这里以一个包含两个目标函数的zdt1问题为例，并别两个目标的重要程度一样，即将权重向量weight设置为[0.5, 0.5]。
（2）使用的分解函数为增强的标量化函数（ASF, Augmented Scalarization Function），它是一个非常有名的多目标评价量。由于这里求解的是最小化问题，所以我们使用ASF()对象的argmin()类方法选择计算后的最小值。

• （1） 获取求解的问题

from pymoo.problems import get_problem

# 定义一个已经准备好的 zdt1 问题
F = get_problem("zdt1").pareto_front()

• （2） 初始化权重和分解函数(decomposition function)

import numpy as np
from pymoo.decomposition.asf import ASF

weights = np.array([0.5, 0.5])
decomp = ASF()

• （3） 使用分解来搜索最佳的值：

I = decomp(F, weights).argmin()
print("Best regarding decomposition: Point %s - %s" % (I, F[I]))

上面三步执行的结果如下图所示：

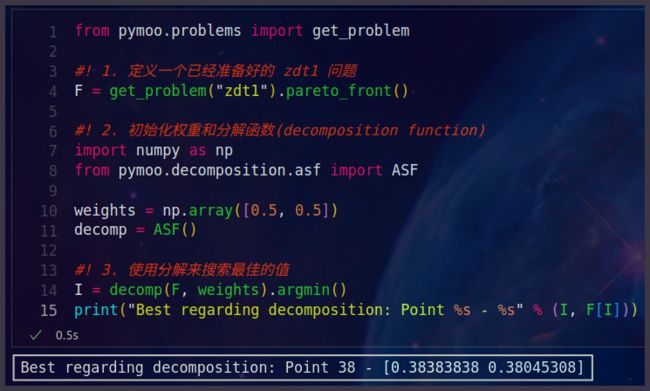
• （4） 结果可视化：

from pymoo.visualization.scatter import Scatter

#! 4. 绘制散点图
plot = Scatter()
#? 添加 zdt1 函数的采样点
plot.add(F, color="blue", alpha=0.2, s=10)
#? 添加最佳决策点 I
plot.add(F[I], color="red", s=30)
plot.do()
plot.apply(lambda ax: ax.arrow(0, 0, 0.5, 0.5, color='black', head_width=0.01, head_length=0.01, alpha=0.4))
plot.show()

代码执行结果如下图所示：

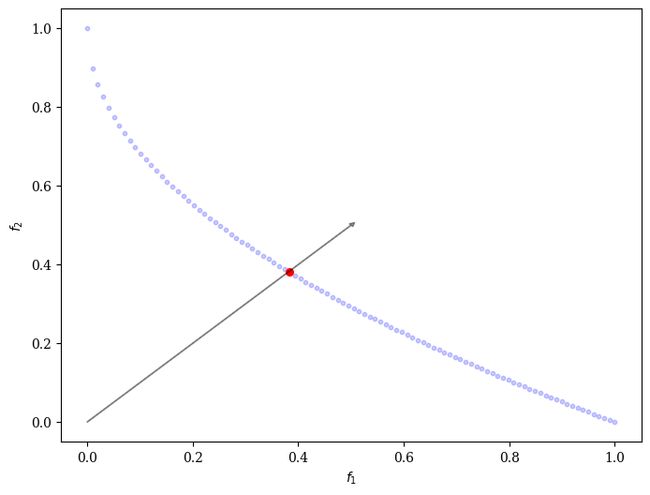
2.2 伪权重方法(Pseudo-Weights)

伪权重方法的具体原理可以参考文献¹（后续有机会，我可以翻译一下），通过下面的公式计算出第$i$个目标函数的伪权重$w_i$：
$$w_i=\frac{(f_i^{max}-f_i(x))/(f_i^{max}-f_i^{min})}{{\sum }_{m=1}^M(f_m^{max}-f_m(x))/(f_m^{max}-f_m^{min})}$$

该方程计算每个目标$i$到最差解的归一化距离（Normalized Distance）。

from pymoo.problems import get_problem
from pymoo.mcdm.pseudo_weights import PseudoWeights
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.petal import Petal
import numpy as np

#! 1. 问题定义：
#? 使用das-dennis方法，定义参考方向
ref_dirs = get_reference_directions("das-dennis", 4, n_partitions=12)
#? 获取问题 dtlz1
F = get_problem("dtlz1").pareto_front(ref_dirs)

#! 2. 初始化权重与权重计算
#* (1) 假设四个方向的重要性一致的情况
weights = np.array([0.25, 0.25, 0.25, 0.25])
#? 使用 PseudoWeights 方法计算决策伪权重
a, pseduo_weights = PseudoWeights(weights).do(F, return_pseudo_weights=True)

#* (2) 假设四个方向的重要性不一致的情况
weights = np.array([0.4, 0.2, 0.15, 0.25])
b, pseduo_weights = PseudoWeights(weights).do(F, return_pseudo_weights=True)

#! 3. 结果可视化
plot = Petal(bounds=(0, 0.5), reverse=True)
plot.add(F[[a, b]])
plot.show()

代码执行结果如下图所示：

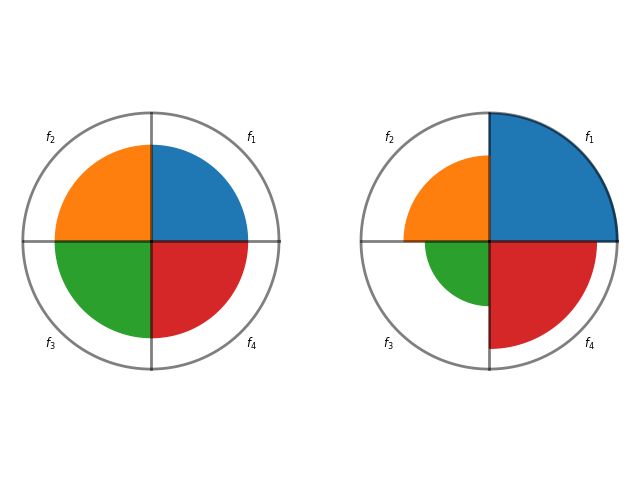
2.3 高折中点(High Trade-off Points)

该方法的具体原理可以参考文献²，pymoo在计算高折中点指标的方法就是参考这篇文献的。下面分别给出3D空间决策的示例：

• （1）获取3D（三目标）Pareto前沿
  我们这里首先应该得到一个多目标优化的一个3D空间的一组Pareto前沿。我的获取方法是，从Stanford 3D 扫描仓库获得 bunny.tar.gz 数据，解压得到 top3.ply 文件，将其放到与脚本文件夹下。截取前400行top3.ply的点阵数据作为Pareto前沿计算结果，代码如下所示：

import numpy as np
from pymoo.visualization.scatter import Scatter
from pymoo.mcdm.high_tradeoff import HighTradeoffPoints
from plyfile import PlyData

# 1. 读取top3.ply点阵文件的前400行数据作为Pareto前沿
plydata = PlyData.read("top3.ply")
pf = np.array([plydata['vertex']['x'], plydata['vertex']['y'], plydata['vertex']['z']])
pf = pf.T
pf = pf[0:400, :]

# 2. 使用HighTradeoffPoints方法计算决策点
dm = HighTradeoffPoints()
I = dm(pf)

# 3. 高折中点计算结果可视化
plot = Scatter(angle=(30, 130))
plot.add(pf, alpha=0.2)
plot.add(pf[I], color="red", s=100)
plot.show()

代码执行结果如下图所示：

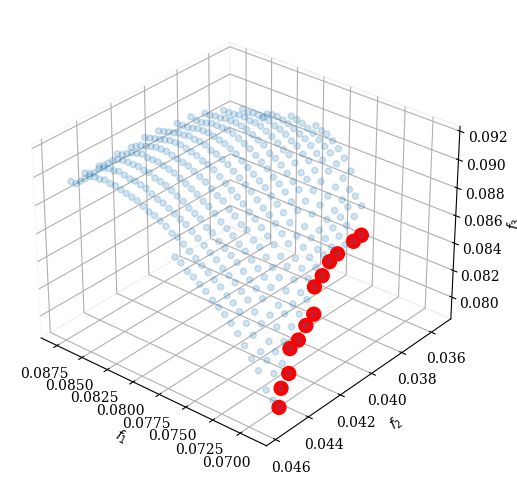
参考文献

---

1. Kalyanmoy Deb and Deb Kalyanmoy. Multi-Objective Optimization Using Evolutionary Algorithms. John Wiley & Sons, Inc., New York, NY, USA, 2001. ISBN 047187339X. ↩︎

2. L. Rachmawati and D. Srinivasan. Multiobjective evolutionary algorithm with controllable focus on the knees of the pareto front. IEEE Transactions on Evolutionary Computation, 13(4):810–824, Aug 2009. ↩︎