BP神经网络Matlab实现(工具箱实现、自主编程实现)
序
BP神经网络是最常见、也是最基础的一种神经网络。网上教程颇多,但是对初学者可能会不太友好。本文打算由浅入深,先使用神经网络工具箱快速实现,然后再自己编写代码加深理解。本文使用 MATLAB 2018B。
一、快速实现
1.1 背景介绍
我们将拟合一个非线性的函数,为简单起见而不失一般性,这个函数有两个自变量,函数为:
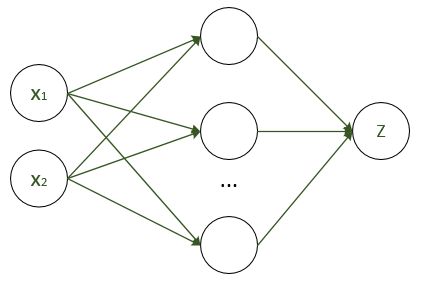
那么,现在神经网络的结构如下:
输入为 x1, x2,输出为 z,中间层数量待定,现需要训练网络,使得各个箭头获得合适的权值,以拟合我们的目标式子。
1.2 神经网络工具箱实现
%% ann_toobox.m
%% 1、模拟产生数据
x1 = -10: 0.2: 10; % 自变量1(行向量)
x2 = -10: 0.2: 10; % 自变量2(行向量)
z = cos(x1) + sqrt(abs(x2))-2; % 真实函数关系
inputs = [x1; x2]; % 输入矩阵(变量数 x 样本数)
targets = z; % 目标矩阵(目标数 x 样本数)
%% 2、训练网络
net = newff(inputs,targets, 50); % 定义网络结构,一个隐含层,含50个神经元
net = train(net,inputs,targets); % 训练网络
outputs = net(inputs); % 训练结果
%% 3、可视化
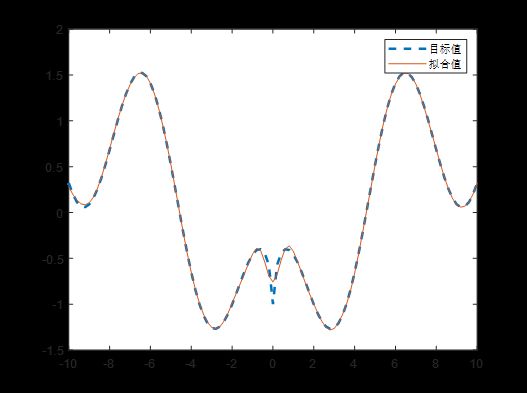
plot(x1, targets,'--','LineWidth', 2); hold on % 绘制真实目标曲线
plot(x1, outputs, 'LineWidth', 1); % 绘制拟合结果
legend('目标值', '拟合值'); hold off % 加图标
结果如下:
可见,整体上已经拟合得很不错了,但是在 0 附近还是有一定偏差。我们可以调节调节网络参数,使得拟合更加准确。
二、更进一步
2.1 归一化
基于以上例子,我们可以做进一步思考和完善。首先是需要归一化,好处有:
- 如果输入值很大,而初始化的权值不变,容易导致非线性变换前的数值太大,梯度消失,不利于训练;
- 输入数据可能量纲不一样,取值范围可能在不同数量级,不利于权值初始化;
一种归一化的方式为
实现了从 x —>y 的映射。这也即 MATLAB 里面的mapminmax()函数,默认归一化到 [-1, 1] 区间。
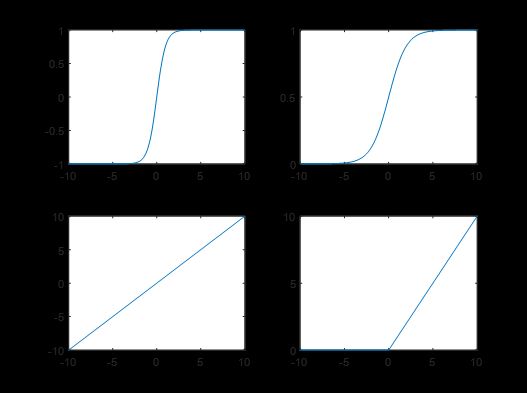
2.2 非线性函数
常用的非线性函数及其图像如下:
遗憾的是,MATLAB似乎只提供前三个,而没有ReLU 函数。在实际工程中,最常用的方式是最后一层使用 tansig,而前面所有层使用ReLU。实际上,ReLU具有
- 单侧抑制
- 相对宽阔的兴奋边界
- 稀疏激活性质(小于零则为零,而不像其他的稍微有点激活)
这些特点其实与生物的神经元有相似之处,自2001年来 ReLU函数成为了后起之秀。
三、自己实现(2020.5.5补充)
3.1 写在前面
其实,关于BP神经网络实现,网上有不少教程,但大多数直接调用工具箱。讲解BP神经网络原理的文章也可以说汗牛充栋。但是,从原理到实例到编程的文章,少之又少。
其实,个人觉得神经网络之所以复杂,其中一个原因就是向量化带来的矩阵运算。如果输入层,隐含层和输出层都只含有一个节点,那么会容易实现很多,包括前向后反向传播,想要自己实现的同行可以先尝试次方案,由浅入深。
为了说明向量化过程,此处以输入层 2 个节点,隐含层 3 个节点,输出层 1 个节点,每次同时输入100个数据训练为例。
为了弄懂原理,务必自己手动计算下面三张图片的过程。没有谁是大神,一眼就能看出里面的矩阵,反正我不能。
如果图片不够清晰,可以在百度网盘链接(链接:https://pan.baidu.com/s/1zo4gm_71OsYxS8G8rgN0kA 提取码:fsyf)下载原图(据说CSDN下载要积分,一个好好的功能就这么废了大半)。
3.2 向量化过程
第一张图片,只考虑一个样本输入,而不是100个样本一起输入的情况。图中包括整个网络结构图,正向传播、部分反向传播。第一层指的是隐含层,第二层值的是输出层。输入层一般不算。注意,图中有的符号,比如 w11 同时是两层的参数,但是注意一下是容易辨识的。为了简洁,牺牲一点精确性是值得的。这里采用经典的 sigma 函数作为激活函数。
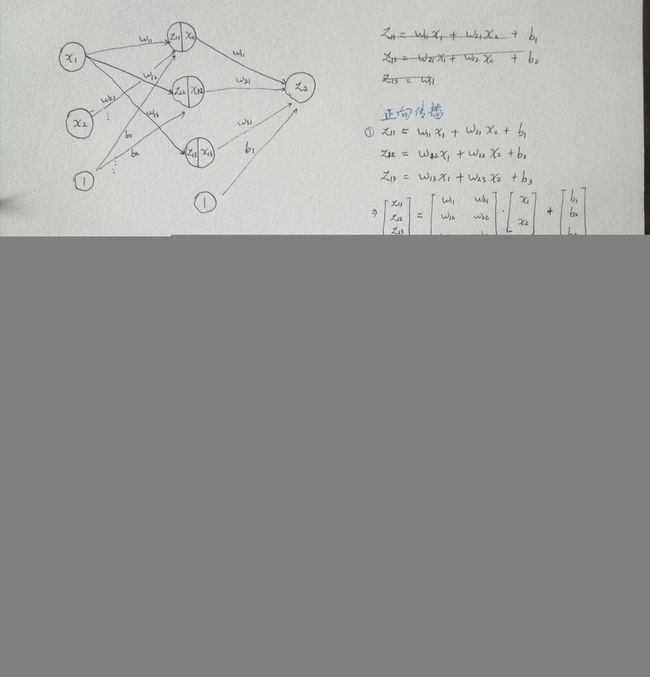
第二张图接着实现剩下的 dW1, db1,并且进行更新。可以看出,最关键的就是求导的链式法则,算好每一个导数,最终的导数自然也有了。注意,这里用星号(*)表示对应元素相乘,用点(·)表示矩阵乘法。
d W 2 = z 2 − t dW_{2} = z_{2} - t dW2=z2−t
特殊点,例如当 z 2 < t z_{2}
W 2 = W 2 − α d W 2 W_{2} = W_{2} - \alpha dW_{2} W2=W2−αdW2
减去一个负数才能增大 W 2 W_{2} W2,因此是减法而不是加。
第三张图片是考虑100个样本同时输入时的情况,图中所有求和都是这100个样本的数据对应求和。这里多引入一个符号(圆圈内加点)表示这一步即含有矩阵的乘法又含有对应元素相乘的方法。随时标注矩阵大小更容易明白整个过程。

3.3 编程实现
弄懂上面三张图片,才有可能自己编写出程序,当然,只想要程序的话,直接看下面程序即可。还是拟合下面的函数,在 [-10, 10] 之间取100个点拟合。
先看效果,看起来不够完美,但是莫方,后面会有改进。
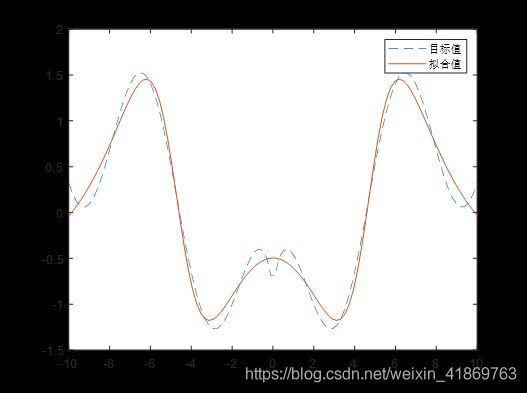
程序如下,里面最难的就是dW2, db2, dW1, db1 的计算,矩阵顺序为什么这样,为什么要转置,这些原因都在上面的图片里。
此外,我觉得使用模块化的思想很重要,这是学习吴恩达《神经网络与深度学习》课程时深刻感受到的。这里也把很多小模块封装成函数,一个个调用,思路更清晰,也方便debug。
rng(0) % 设定随机数种子,保证可重复性
m = 2; % 输入层数量
n1 = 5; % 隐含层数量
n2 = 1; % 输出层数量
N = 100; % 并行输入样本数
x = [linspace(-10, 10, N); % 目标函数的 x1
linspace(-10, 10, N)]; % 目标函数的 x2
t = cos(x(1,:))+ sqrt(abs(x(2,:)))-2; % 目标值
x1 = mapminmax(x); % 归一化
W1 = randn(n1, m); % 随机初始化参数 W1
b1 = randn(n1, 1); % 随机初始化参数 b1
W2 = randn(n2, n1); % 随机初始化参数 W2
b2 = randn(n2, 1); % 随机初始化参数 b2
alpha = 0.001; % 学习率,可调节查看效果
for k = 1:50000 % 训练50000次
z1 = forward_linear(x1, W1, b1); % 前向线性变换
x2 = forward_nonlinear(z1); % 非线性变换
z2 = forward_linear(x2, W2, b2); % 前向线性变换
E = sum_err_squ(z2, t); % 计算误差
if E < 0.01
break; % 误差小于给定值,退出
end
[dW2, db2] = backward_w2b2(z2, t, x2); % 计算参数增量
[dW1, db1] = backward_w1b1(z2, t, W2, x2, x1); % 计算参数增量
W2 = W2 - alpha * dW2; % 更新参数
b2 = b2 - alpha * db2; % 更新参数
W1 = W1 - alpha * dW1; % 更新参数
b1 = b1 - alpha * db1; % 更新参数
end
plot(x(1,:), t, '--',x(1,:), z2); % 绘图
legend('目标值', '拟合值');
function z = forward_linear(x, W, b) % 前向线性变换
z = W * x + b;
end
function x = forward_nonlinear(z) % 前向非线性变换
x = 1 ./ (1 + exp(-z));
end
function E = sum_err_squ(z2, t) % 误差平方和
E = 1/2 * sum((z2 - t).^2);
end
function [dW2, db2] = backward_w2b2(z2, t, x2) % 参数增量 dW2, db2
dW2 = (z2 - t) * x2';
db2 = sum(z2 - t);
end
function [dW1, db1] = backward_w1b1(z2, t, W2, x2, x1) % 参数增量 dW1, db1
dW1 = (z2 - t) .* (W2' .* x2 .* (1-x2)) * x1';
db1 = (W2' .* x2 .* (1-x2)) * (z2 - t)';
end
运行结果已经在上面了。可是尝试改变隐含层神经元数量,学习因子 alpha 来看看不同的效果。
3.4 改进
曲线总是拟合得不够好,其实一个原因是学习率是固定的,这又个缺点,学习率太小训练缓慢,学习率太大精度有限。因此,我们希望刚开始学习率大些,后期学习率小些,一种方法是给定学习率函数,但是比较复杂。动量因子法是经过历史考验传承下来的方法,因此采用。
依旧是简单看下原理:
之前的更新公式: W 2 = W 2 − α ∗ d W 2 W_{2} = W_{2} - \alpha*dW_{2} W2=W2−α∗dW2
使用动量法的更新公式: d W 2 = m ⋅ d W 2 ^ + α ⋅ d W 2 dW_{2} = m\cdot \hat{dW_{2}} + \alpha \cdot dW_{2} dW2=m⋅dW2^+α⋅dW2
W 2 = W 2 − d W 2 W_{2} = W_{2} - dW_{2} W2=W2−dW2
其中 m m m 是动量因子, d W 2 ^ \hat{dW_{2}} dW2^ 是上一次的误差量,也即梯度。
简单说, W 2 W_{2} W2 的最终增量从 α ∗ d W 2 \alpha*dW_{2} α∗dW2 变为 m ⋅ d W 2 ^ + α ⋅ d W 2 m\cdot \hat{dW_{2}} +\alpha \cdot dW_{2} m⋅dW2^+α⋅dW2
这样的好处是什么呢?能够延续上一次的梯度。上一次梯度和这一次梯度都为正,这一次也将会有很大正的梯度,而且越加越快,加快刚开始时的网络收敛速度。后期某一次上次梯度为正,这次为负,那么一次又一次地负梯度打击下,梯度绝对值将逐渐减小,最后到 0 附近,可能收敛了,也可能继续往负方向越来越快地增大。但最终,网络收敛时,梯度接近0。
说了那么多,先看效果(其他条件不变),使用动量(动量因子0.9)后好一些:
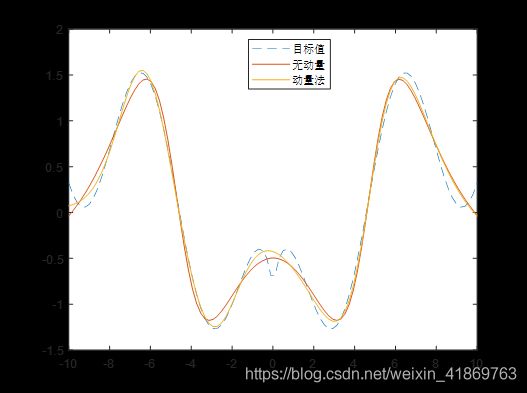 程序如下:
程序如下:
rng(0) % 设定随机数种子
m = 2; % 输入层数量
n1 = 5; % 隐含层数量
n2 = 1; % 输出层数量
N = 100; % 并行输入样本数
x = [linspace(-10, 10, N); % 目标函数的 x1
linspace(-10, 10, N)]; % 目标函数的 x2
t = cos(x(1,:))+ sqrt(abs(x(2,:)))-2; % 目标值
x1 = mapminmax(x); % 归一化
W1 = randn(n1, m); % 随机初始化参数 W1
b1 = randn(n1, 1); % 随机初始化参数 b1
W2 = randn(n2, n1); % 随机初始化参数 W2
b2 = randn(n2, 1); % 随机初始化参数 b2
alpha = 0.001; % 学习率,可调节查看效果
m = 0.9;
dW2 = zeros(size(W2));
db2 = zeros(size(b2));
dW1 = zeros(size(W1));
db1 = zeros(size(b1));
for k = 1:50000 % 训练50000次
z1 = forward_linear(x1, W1, b1); % 前向线性变换
x2 = forward_nonlinear(z1); % 非线性变换
z2 = forward_linear(x2, W2, b2); % 前向线性变换
E = sum_err_squ(z2, t); % 计算误差
if E < 0.01
break; % 误差小于给定值,退出
end
dW2_last = dW2; % 记录上次 dW2
db2_last = db2;
dW1_last = dW1;
db1_last = db1;
[dW2, db2] = backward_w2b2(z2, t, x2); % 计算参数增量
[dW1, db1] = backward_w1b1(z2, t, W2, x2, x1); % 计算参数增量
dW2 = m * dW2_last + alpha * dW2; % 动量法更新 dW2
db2 = m * db2_last + alpha * db2;
dW1 = m * dW1_last + alpha * dW1;
db1 = m * db1_last + alpha * db1;
W2 = W2 - dW2; % 更新参数
b2 = b2 - db2; % 更新参数
W1 = W1 - dW1; % 更新参数
b1 = b1 - db1; % 更新参数
end
plot(x(1,:), t, '--',x(1,:), z2); hold on % 绘图
legend('目标值', '拟合值');
function z = forward_linear(x, W, b) % 前向线性变换
z = W * x + b;
end
function x = forward_nonlinear(z) % 前向非线性变换
x = 1 ./ (1 + exp(-z));
end
function E = sum_err_squ(z2, t) % 误差平方和
E = 1/2 * sum((z2 - t).^2);
end
function [dW2, db2] = backward_w2b2(z2, t, x2) % 参数增量 dW2, db2
dW2 = (z2 - t) * x2';
db2 = sum(z2 - t);
end
function [dW1, db1] = backward_w1b1(z2, t, W2, x2, x1) % 参数增量 dW1, db1
dW1 = (z2 - t) .* (W2' .* x2 .* (1-x2)) * x1';
db1 = (W2' .* x2 .* (1-x2)) * (z2 - t)';
end
3.5 炼丹师的工作
慢慢调节隐含层数目、动量因子、学习率、初始化参数这些,如果有能力,连激活函数改了(记得反向传播公式也要修改)或许能够找到一组好的参数。深度学习工程师(炼丹师)就是做这个的。调了一组,效果如下:
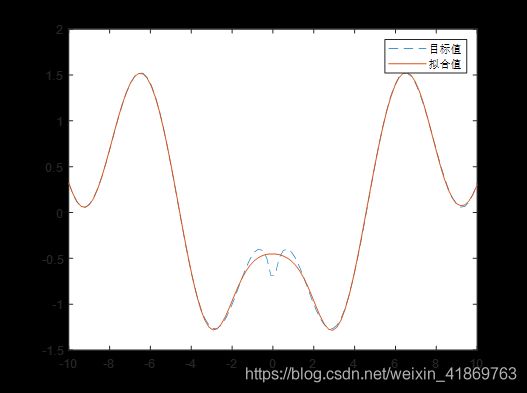
比其刚开始的使用工具箱的那张,效果差些,但是勉强可以接受了。代码附上:
rng(0) % 设定随机数种子
m = 2; % 输入层数量
n1 = 8; % 隐含层数量
n2 = 1; % 输出层数量
N = 100; % 并行输入样本数
x = [linspace(-10, 10, N); % 目标函数的 x1
linspace(-10, 10, N)]; % 目标函数的 x2
t = cos(x(1,:))+ sqrt(abs(x(2,:)))-2; % 目标值
x1 = mapminmax(x); % 归一化
W1 = randn(n1, m) / 10; % 随机初始化参数 W1
b1 = randn(n1, 1) / 10; % 随机初始化参数 b1
W2 = randn(n2, n1) / 10; % 随机初始化参数 W2
b2 = randn(n2, 1) / 10; % 随机初始化参数 b2
alpha = 0.008; % 学习率,可调节查看效果
m = 0.90;
dW2 = zeros(size(W2));
db2 = zeros(size(b2));
dW1 = zeros(size(W1));
db1 = zeros(size(b1));
for k = 1:50000 % 训练50000次
z1 = forward_linear(x1, W1, b1); % 前向线性变换
x2 = forward_nonlinear(z1); % 非线性变换
z2 = forward_linear(x2, W2, b2); % 前向线性变换
E = sum_err_squ(z2, t); % 计算误差
if E < 0.01
break; % 误差小于给定值,退出
end
dW2_last = dW2; % 记录上次 dW2
db2_last = db2;
dW1_last = dW1;
db1_last = db1;
[dW2, db2] = backward_w2b2(z2, t, x2); % 计算参数增量
[dW1, db1] = backward_w1b1(z2, t, W2, x2, x1); % 计算参数增量
dW2 = m * dW2_last + alpha * dW2; % 动量法更新 dW2
db2 = m * db2_last + alpha * db2;
dW1 = m * dW1_last + alpha * dW1;
db1 = m * db1_last + alpha * db1;
W2 = W2 - dW2; % 更新参数
b2 = b2 - db2; % 更新参数
W1 = W1 - dW1; % 更新参数
b1 = b1 - db1; % 更新参数
end
plot(x(1,:), t, '--',x(1,:), z2); % 绘图
legend('目标值', '拟合值');
function z = forward_linear(x, W, b) % 前向线性变换
z = W * x + b;
end
function x = forward_nonlinear(z) % 前向非线性变换
x = 1 ./ (1 + exp(-z));
end
function E = sum_err_squ(z2, t) % 误差平方和
E = 1/2 * sum((z2 - t).^2);
end
function [dW2, db2] = backward_w2b2(z2, t, x2) % 参数增量 dW2, db2
dW2 = (z2 - t) * x2';
db2 = sum(z2 - t);
end
function [dW1, db1] = backward_w1b1(z2, t, W2, x2, x1) % 参数增量 dW1, db1
dW1 = (z2 - t) .* (W2' .* x2 .* (1-x2)) * x1';
db1 = (W2' .* x2 .* (1-x2)) * (z2 - t)';
end
完!