机器学习复习

第一章 绪论

1、机器学习定义

机器学习致力于研究如何通过计算的手段，利用经验来改善系统自身的性能。

2、机器学习的过程、框架

模型、策略、算法

3、机器学习分类

按照训练数据是否有标记信息

监督学习：回归问题、分类问题 有标记
非监督学习：聚类问题 无标记

监督学习	非监督学习
线性回归	聚类算法
对数几率回归	原型聚类（k均值、学习向量量化、高斯混合聚类）
决策树	密度聚类
神经网络	层次聚类
支持向量机
贝叶斯分类器

4、机器学习目标

使得学得的模型更好地适用于“新样本”。适用于新样本的能力，称之为泛化能力

5、基本术语

• 数据集：训练集、测试集
• 示例、样例
• 样本
• 属性、特征；属性值
• 属性空间、样本空间、输入空间
• 特征向量
• 标记空间、输出空间
• 假设空间

第二章 模型的评估与选择

1、错误率和精度

错误率： 分类错误的样本数占总样本数的比例
精度： 1-错误率

2、误差

学习器的实际预测输出与样本的真实输出之间的差异

泛化误差： 在新样本上的误差
经验误差： 在训练集上的误差（训练误差）

泛化误差越小越好
经验误差过小会导致过拟合

3、过拟合和欠拟合的概念

过拟合： 学习能力过于强大，以至于把训练样本所包含的不太一般的特性都学到了
欠拟合： 通常由学习能力低下造成

4、正则化

正则化的主要目的是控制模型复杂度，减小过拟合。

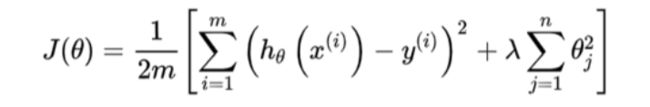
其中，λ为正则化参数

5、模型选择的三个关键问题

• 评估方法
• 性能度量
• 比较检验

6、评估方法

• 留出法
• 交叉验证法
• 自助法

7、留出法

给定n个样本，一半做训练，一半做测试，则训练误差和测试误差之间的差距会随n的增大而减小

注意：

• 保持数据分布的一致性（分层抽样）
• 多次重复划分
• 测试集不能太大、不能太小（1/5~1/3）

8、k-折交叉验证法

过程： 先将数据集划分为k个大小相似的互斥子集，每个子集都尽可能保持数据分布的一致性，即从数据集中通过分层抽样得到。然后每次用k-1个子集的并集作为训练集，余下那个子集作为测试集，这样就可获得k组训练/测试集，从而进行k次训练和测试，最终返回的是这k个测试结果的均值。

9、自助法

基于自助采样，也称“有放回采样”、“可重复采样”
约有36.8%的样本不会在训练集中出现，称为包外估计

10、“调参”与最终模型

算法的参数：一般由人工设定，亦称“超参数”
模型的参数：一般由学习确定

区别：
训练集：
测试集：
验证集：为了加以区分，模型评估与选择中用于评估测试的数据集称为“验证集”

我们用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和验证集，基于验证集上的性能来进行模型的选择和调参。

11、性能度量

性能度量是衡量模型泛化能力的评价标准，反映了任务需求
使用不同的性能度量往往会导致不同的评判结果

回归任务：	分类任务：
均方误差	错误率与精度
	查准率、查全率与F1
	ROC与AUC
	代价敏感错误率与代价曲线

均方误差：
混淆矩阵

TP——将正类预测为正类数
FN——将正类预测为负类数
FP——将负类预测为正类数
TN——将负类预测为负类数

查准率：P=TP/（TP+FP）
查全率：R=TP/（TP+FN）

例题：有100个样本，其中有80个正样本，20个负样本。预测出70个正样本，30个负样本。其中60个预测正确的正样本，10个预测正确的负样本，计算P和R。

9、PR图

纵坐标是查准率
横坐标是查全率

10、ROC曲线和AUC

ROC曲线下面的面积用AUC表示
AUC越大，模型的训练效果越好

11、误差

包含偏差、方差和噪音

• 偏差：期望输出与真实输出的差别，刻画了学习算法本身的拟合能力
• 方差：同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响
• 噪声：刻画了学习问题本身的难度
  偏差和方差都比较小时，泛化能力比较好。

第三章 线性模型

1、基本形式

线性模型试图学得一个通过属性的线性组合来进行预测的函数

2、线性回归

策略：使均方误差最小
算法：最小二乘法、梯度下降法

均方误差：预测值与真实值之间差的平方
最小二乘法：基于均方误差最小化来进行模型求解的方法

梯度下降法：
三要素：
假设：
目标函数：
优化算法：给定训练集，如何找到参数使得目标函数最小

学习率α对梯度下降的影响
α太小：梯度下降收敛速度过慢
α太大：梯度下降则不会收敛，振荡或者发散

3、对数几率回归

解决分类问题
sigmod函数：把样本的输出值转为0-1之间
输出的含义：对于输入x，输出表示x的标签为1的可能性

4、多分类学习

拆解法： 将一个多分类任务拆分为若干个二分类任务求解
拆分策略：

• 一对多：如果有k个类别，则训练k个分类器
• 一对一：如果有k个类别，则训练k（k-1）/2个分类器
• 多对多

第四章 决策树

1、概念

决策树基于树结构进行决策
内部结点：对应某个属性上的测试
分支：对应该测试的一种可能结果（即该属性的某个取值）
叶子结点：对应一个预测结果

2、学习过程

通过对训练样本的分析来确定“划分属性”

3、预测过程

将测试示例从根节点开始，沿着划分属性所构成的“判定序列”下行，直到叶节点。

4、基本流程

策略：“分而治之”
自根至叶的递归过程
在每个中间结点寻找一个“划分”属性
三种停止条件：
（1）当前结点包含的样本全属于同一类别
（2）当前属性集为空，或是所有样本在所有属性上的取值相同
（3）当前节点包含的样本集为空，不能划分

5、划分选择

信息增益

信息熵

值越小，信息纯度越高
Ent（D）最小为0，D只有一类
最大为log2|y|，每个都是一类

信息增益

信息增益越大，结果越好
对可取值数目较多的属性有所偏好

增益率
对可取值数目较少的属性有所偏好
增益率越大，结果越好

基尼系数
基尼指数越小，数据集纯度越高

6、剪枝

可通过主动去掉一些分支来降低过拟合的风险
基本策略：
预剪枝：在决策树生成的过程中，对每个结点在划分之前先进行估计，若当前节点的划分属性不能带来泛化性能的提升，则停止划分，并将当前节点记为叶子结点
后剪枝：先从训练集生成一个完整的决策树，然后自底向上对非叶子结点进行考察，若将该节点对应的子树替换为叶子节点能带来泛化性能的提升，则将该子树替换为叶子结点。

第五章 神经网络

1、M-P神经元模型

在这个模型中，神经元接收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元收到的总输入值将于神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出。

2、感知机

感知机由两层神经元组成
感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元。不能解决非线性可分问题。与、或、非可以，异或不行。

3、神经网络

学习过程：利用事先提供的训练数据，来调整神经元之间的连接权，以及每个功能神经元的阈值，这在神经网络中称为学习。

4、误差逆传播算法（BP）

权重和阈值参数
输入层的神经元不是功能神经元，没有阈值

给定一个模型，计算有多少个参数：
输入层d个神经元，隐藏层q个神经元，输出层l个神经元
权重：d * q+q * l
阈值：q+l

5、BP算法

基于梯度下降策略，以目标的负梯度方向对参数进行调整。BP算法是一个迭代学习算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计。
算法流程

• 首先，随机初始化网络中所有的连接权和阈值参数
• 然后进行迭代更新
• 在每次更新的时候，对所有的训练样本，先去计算它当前的输出，根据当前的输出，计算出隐藏层和输出层神经元的梯度项
• 最后更新连接权和阈值参数
• 一直到达终止条件。（可以设置终止条件，比如最大迭代次数）

6、缓解BP算法的过拟合问题

主要策略：
早停： 若训练误差连续a轮的变化小于b，则停止训练
若训练集误差降低但验证集误差升高，则停止训练
正则化： 降低模型复杂度，来缓解过拟合
在误差目标函数中增加一个用于描述网络复杂度的部分

第六章 支持向量机

1、间隔与支持向量

超平面方程：wT