NC：基于38组数据评估14种微生物组差异分析方法—结果差异很大

微生物组差异丰度方法在38个数据集上产生了不同的结果

Microbiome differential abundance methods produce disturbingly different results across 38 datasets

DOI：https://doi.org/10.1038/s41467-022-28034-z

Nature Communications [IF: 14.919]

发表日期：2022-01-17

第一作者: Jacob T. Nearing¹,Gavin M. Douglas¹

通讯作者：Jacob T. Nearing([email protected])¹

合作作者: Molly G. Hayes, Jocelyn MacDonald, Dhwani K. Desai, Nicole Allward, Casey M. A. Jones, Robyn J. Wright, Akhilesh S. Dhanani, André M. Comeau, Morgan G. I. Langille

主要单位：¹加拿大达尔豪斯大学(Department of Microbiology and Immunology, Dalhousie University, Halifax, NS, Canada)

摘要

识别丰度差异的微生物是微生物组研究的共同目标。在文献中，为达到这个目的可以使用多种方法。然而，很少有大规模的研究系统地探讨交替使用这些工具的适当性，以及它们结果之间差异的规模和意义。在此，我们在两个样本组的38个16S rRNA基因数据集上比较14种检测丰度差异的方法的性能。我们检测了这些组之间扩增子序列变体(ASV)和操作分类单位(OTU)的差异。我们的发现证实，这些工具识别出的显著ASV的数量以及集合存在显著差异，并且结果取决于数据预处理。对于许多工具而言，所识别特征的数量与数据的特征相关，例如样本大小、测序深度和群落差异的影响大小。ALDEx2和ANCOM-II在所有研究中得出的结果最一致，与不同方法得出的结果的交集最一致。然而，我们建议研究人员应使用基于多重差异丰度方法的共识方法，以帮助确保稳健的生物学解释。

背景

微生物组通常以DNA序列为特征。标记基因测序，如16S rRNA基因测序，是微生物组分析最常见的形式，可用于比较不同样本中分类群的相对丰度。使用这类数据进行研究时，一个常见且看似简单的问题是:哪些分类群在样本分组之间的相对丰度存在显著差异？微生物组领域的新手可能会惊讶地发现，在如何最好地解决这个问题上几乎没有共识。事实上，关于使用微生物组数据进行差异丰度(differential abundance，DA)检测的最佳实践，目前存在许多持续的争论。

存在分歧的一个领域是，读长(read)计数表是否应进行稀释(即二次采样)，以校正样本间的不同读长深度。 这种方法受到了严厉的批评，因为排除数据可能会降低统计能力并引入偏见。特别是，将稀释后的计数表用于标准检测，如t-检验和Wilcoxon检验，可能会导致不可接受的高假阳性率。尽管如此，微生物组数据仍经常被稀释，因为它可以简化分析，特别是对于不控制样本间read深度变化的方法。例如，LEfSe是鉴定差异丰富分类群的常用方法，它首先将读长计数转换为百分比。因此，读长计数表在输入到该工具之前通常会被稀释，以便样本读长深度的变化不会影响分析。如果不通过某种方法解决样本之间的深度差异，仅由于读长深度，样本之间的丰富度可能会有很大差异。

一个与数据是否应该稀释相关的问题是稀有分类群是否应该被过滤掉。 这个问题出现在许多高通量数据集上，在这些数据集上，对许多测试进行校正的负担会大大降低统计能力。在运行统计测试之前，过滤掉可能没有信息的特征有助于解决这个问题，尽管在某些情况下，这也会产生意想不到的效果，比如增加误报。重要的是，此过滤必须独立于评估的测试统计(称为独立过滤)。例如，通常使用样本间(而非一组与另一组之间)分类群流行率(prevalence)和丰度的硬界限来排除稀有分类群。这种数据过滤对于微生物组数据集尤其重要，因为它们通常极其稀疏。尽管如此，尚不清楚在实践中筛选稀有分类群是否对DA结果有很大影响。

另一个有争议的领域是哪些统计分布最适合分析微生物组数据。已经开发了基于一系列分布的统计框架来对读长计数数据进行建模。例如，DESeq2和edgeR都是假设读长计数遵循负二项分布的工具。为了识别丰度差异的分类单元，对每个分类单元比较一个零假设（null hypothesis）和备择假设（alternative hypothesis）。零假设表明，负二项式解的某些参数的相同设置解释了所有样本分组中的分类群分布。备择假设指出，需要不同的参数设置来说明样本分组之间的差异。如果某一特定分类单元的零假设可以被拒绝，那么它被认为是丰度是差异的。这一思想是基于分布的DA(distribution-based DA)检验的基础，也包括其他方法，如corncob和metagenomeSeq，它们分别用β-二项式分布和零膨胀高斯分布(beta-binomial and zero-inflated Gaussian distributions)对微生物组数据建模。

最后，最近人们越来越广泛地认识到测序数据是组成性的，这意味着测序只提供了特征相对丰度的信息，并且每个特征的观测丰度取决于所有其他特征的观测丰度。这一特征意味着当用于绝对丰度的标准方法与分类相对丰度一起使用时，通常会做出错误的推断。成分数据分析(Compositional data analysis，CoDa)方法通过将分析重点重新定位于样本中不同分类群之间的读长计数比率，从而规避了这一问题。本文所考虑的各种CoDa方法之间的不同之处在于将丰度值用作转换的分母或参考值。居中对数比(centered
log-ratio，CLR)转换是一种CoDa方法，使用样本中所有分类群的读长计数的几何平均值作为该样本的参考/分母。在这种方法中，样本中的所有分类单元读长计数都用这个几何平均值来划分，并比较样本之间这个比值的对数倍数变化。这种方法的扩展在工具ALDEx2中实现。加性对数比转换(additive log-ratio transformation)是一种替代方法，它的参考值是单个分类单元的计数丰度，在样本间的读长计数中应呈现低方差。在这种情况下，所选择的参考分类单元(分母)与该样本中每个分类单元之间的比率在不同样本分组之间进行比较。ANCOM是实现这种加性对数比转换方法的一种工具。

尽管有上述选择，但已证明难以评估用于分析微生物组数据的众多方案。这在很大程度上是因为没有黄金标准来比较DA工具的结果。用差异丰富的特定分类群模拟数据集是解决这个问题的部分方法，但并不完美。例如，已经注意到参数模拟可能导致特定工具的循环论证，从而难以评估它们的真实性能。毫不奇怪，基于分布的方法在应用于基于该分布的模拟数据时表现最佳。尽管如此，没有预期差异的模拟数据对于评估这些方法的错误发现率(FDR)一直很有价值。基于这种方法，很明显许多方法产生不可接受的高数量的假阳性识别。同样，基于含有加标分类群（spiked taxa）的模拟数据集，研究表明这些方法的统计能力可能存在巨大差异。

尽管这些一般性意见得到了很好的证实，但在各种评价研究中，对工具的性能的一致意见较少。某些观察结果是可再现的，如edgeR和metagenomeSeq的FDR更高。同样，ALDEx2已反复显示出检测差异的能力较低。相比之下，根据研究的不同，ANCOM和limma voom都被认为是准确和不良地控制了FDR。为了使比较更为复杂，对不同评估研究中的不同工具集和数据集类型进行了分析。这意味着，在某些情况下，一个评估中表现最好的方法会从另一个评估中消失。此外，过去的评估中遗漏了某些流行的微生物组特异性方法，如MaAsLin2。最后，许多评估将其分析局限于少数数据集，这些数据集不代表16S rRNA基因测序研究中发现的数据集的广度。

鉴于这些研究之间的不一致性，进行额外的独立评估以阐明当前DA方法的性能非常重要。这一点尤其重要，因为这些工具在微生物组研究中通常可互换使用。因此，我们在此对38个两组16S rRNA基因数据集的常用DA工具进行了额外评估。我们首先介绍了这些数据集上方法的一致性，以研究这些方法在去除稀有分类群和不去除稀有分类群的情况下，聚类和总体表现的一致性。接下来，在将数据集人工二次采样为两组(不存在预期差异)的基础上，我们给出了每个DA工具的观测假阳性率。最后，我们评估了腹泻和肥胖数据集之间生物学解释的一致性，这取决于所应用的工具。我们的工作改进了对这些DA工具的评估，并强调了在独立评估中应采纳先前研究中提出的哪些关键建议。此外，我们的分析显示了DA工具的各种特征，作者可以使用这些工具来评估该领域的已发表文献。

结果

识别出显著的ASV数量的高度可变性

为了研究不同DA工具如何影响微生物组数据集的生物学解释，我们在38个不同的微生物组数据集(共9405个样本)上测试了14种不同的DA测试方法(表1)。这些数据集对应于一系列环境，包括人类肠道、塑料球、淡水、海洋、土壤、废水和建筑环境。这些数据集中的特征既对应于ASV，也对应于OTU，但为了简单起见，我们将它们都称为ASV。

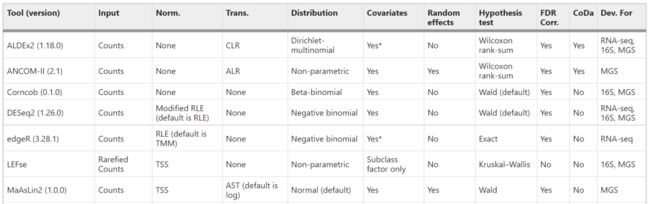
表1 本研究中差异丰度工具的比较

*该工具支持其他协变量(如果提供)。在这种情况下，ANCOM-II 会自动执行 ANOVA，ALDEx2 要求用户选择测试，edgeR 需要使用不同的函数(glmFit 或 glmQLFit 而不是 exactTest)。

ALR 加性对数比，AST 反正弦平方根变换，CLR 中心对数比，CoDa 成分数据分析，CSS 累积和缩放，FDR Corr. 错误发现率校正，MGS 宏基因组测序，RLE 相对对数表达，TMM 调整的M值平均值，Trans. 变换，TSS 总和缩放。

我们还研究了在分析之前过滤每个数据集的流行率（frequency）如何影响观察到的结果。我们选择使用不使用流行率过滤(图1a)或10%流行率过滤，以去除在每个数据集中不到10%的样本中发现的任何ASV(图1b)。

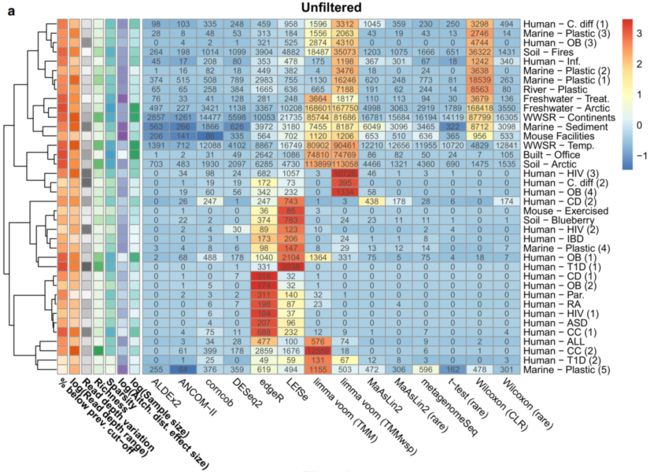
图1 显著特征比例的变化取决于鉴定差异丰度的方法和数据集

热图显示了根据A未过滤数据和B10%流行率过滤后的数据通过相应工具在每个数据集中鉴定出的显著扩增子序列变异体(ASV)的数量。根据每个数据集的显著ASV的标准化(按比例缩放和以平均值为中心)百分比对单元格进行着色。最左边六列中的其他彩色单元格表示我们假设可能导致这些结果变化的数据集特征(较暗的颜色表示较高的值)。使用完全方法，基于欧几里德距离对数据集进行分层聚类。缩写：prev., previous；TMM，M值的修剪平均值(trimmed mean of M-values)；TMMwsp，具有单例配对的M值的修剪平均值(trimmed mean of M-values with singleton pairing)；rare，rarefied；CLR，center-log-ratio。源数据以源数据文件的形式提供。

我们发现，在过滤和未过滤分析中，通过每种DA方法识别的显著ASV百分比在不同数据集之间差异很大，平均值分别在3.8–32.5%和0.8–40.5%之间。有趣的是，我们发现许多工具在不同的数据集上表现不同。具体而言，一些工具在一个数据集中识别出大多数特征，而在其他数据集中仅识别出一个中间数量（intermediate number）的特征。这在未过滤的数据集上尤其明显(图1a)。

尽管工具性能在数据集之间存在可变性，但我们确实发现有几种工具倾向于识别更显著的命中(hits)。在未过滤的数据集中，我们发现与其他方法相比，limma voom(TMMwsp；平均:40.5%；SD:41% / TMM；平均:29.7%；SD: 37.5%)，Wilcoxon(CLR；平均:30.7%；SD: 42.3%)、LEfSe(平均:12.6%)；SD: 12.3%)，edgeR(平均:12.4%，SD: 11.4%)倾向于发现最多数量的显著ASV。有趣的是，在一些数据集，如Human-ASD和Human-OB数据集中，edgeR发现显著ASV的比例高于任何其他工具。此外，我们发现limma voom (TMMwsp)发现大多数ASV在Human-HIV 数据集中具有显著性(73.5%)，而其他工具发现0-11%的显著ASV(图1)。我们发现，两种limma voom方法均确定超过99%的ASV在若干情况下具有显著性，如Built-Office和Freshwater-Arctic数据集。这很可能是由于这些数据集的高度稀疏性导致工具的参考样本选择方法(上四分位数归一化)失败。Wilcoxon (CLR)输出中也发现了此类极端发现，其中超过90%的ASV在八个独立数据集内被称为显著。我们发现了与LEfSe类似的趋势，尽管不那么极端，其中在一些数据集(如Human-T1D 数据集)中，与所有其他工具(0–0.4%)相比，该工具发现了高得多的显著命中百分比(3.5%)。这一观察结果很可能是因为LEfSe按效应大小过滤显著特征，而不是使用FDR校正来减少假阳性的数量。我们发现，在我们测试的三种组成性方法中，有两种比其他测试工具识别出更少的显著ASV。具体而言，ALDEx2(平均:1.4%；SD: 3.4%)和ANCOM-II(平均:0.8%；SD: 1.8%)确定了最少的显著ASV。我们发现这些工具的保守行为在我们测试的所有38个数据集上是一致的。

总体而言，基于过滤表的结果相似，尽管每个工具识别的显著ASV特征数量范围较小。与未过滤的数据集相比，除ALDEx2之外的所有工具均发现总显著特征数较低。与未过滤的数据一样，ANCOM-II是最严格的方法(平均值:3.8%；SD: 5.9%)，edgeR(平均:32.5%；SD: 28.5%)、LEfSe(平均:27.5%；SD: 25.0%)、limma voom(TM mwsp；平均:27.3%；SD:30.1%；TMM；平均:23.5%；SD: 27.7%)、Wilcoxon(CLR；平均:25.4%；SD: 31.7%)倾向于输出最高数量的显著ASV(图1b)。

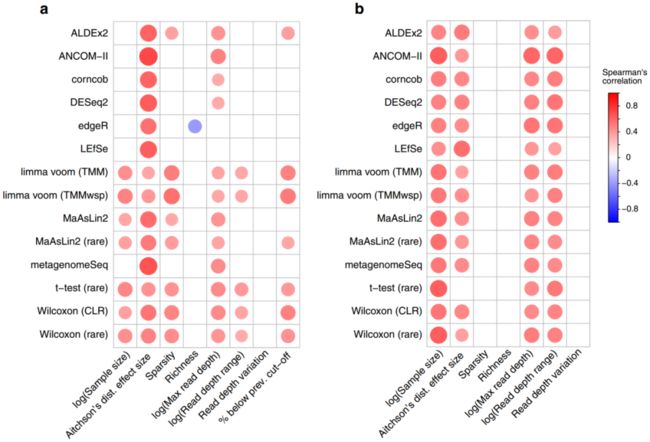
为了研究导致这种差异的可能因素，我们研究了每种工具所识别的ASV数量与几个变量之间的相关性。 这些变量包括数据集丰富度(dataset richness)、样本间测序深度的变化、数据集稀疏度和艾奇逊(Aitchison)距离效应大小(基于PERMANOVA检验)。正如预期，我们发现所有工具识别的ASV数量与试验组之间的效应大小呈正相关，未过滤数据的Spearman相关系数值在0.35–0.72之间(图2a)，过滤数据的Spearman相关系数值在0.31–0.56之间(图2b)。我们还在筛选的数据集内发现，所有工具发现的ASV数量与中位read深度、read深度范围和样本大小显著相关。未过滤数据之间的相关性不太一致。例如，只有t检验、Wilcoxon方法和limma voom方法与read深度范围显著相关(图2b)。我们还发现，在未过滤分析中，edgeR与平均样本丰富度呈负相关。未过滤数据集中低于10%流行率的ASV百分比也与几种工具的输出显著相关。我们还研究了嵌合体是否会影响检测到的显著ASV的数量，结果显示影响非常有限。

图2 与显著扩增子序列变异百分比相关的数据集特征

按大小和颜色显示A未过滤和B流行率过滤数据的相关系数(Spearman rho)。这些与数据集特征相对应，数据集特征与通过该工具鉴定的每个数据集的显著扩增子序列变体的百分比相关。仅显示多次比较校正前的显著相关性(p < 0.05)。缩写:prev., previous；TMM，M值的修剪平均值(trimmed mean of M-values)；TMMwsp，具有单例配对的M值的修剪平均值(trimmed mean of M-values with singleton pairing)；rare，rarefied；CLR，center-log-ratio。源数据以源数据文件的形式提供。

接下来，我们研究了通过测试DA工具识别的显著ASV是否平均具有不同的相对丰度。最明显的异常值是ALDEx2(显著ASV的中位相对丰度:0.013%)、ANCOM-II(中位:0.024%)以及在较小程度上的DESeq2(中位:0.007%)，这些异常倾向于发现未过滤数据集内相对丰度较高的显著特征。在过滤后的数据集内，ALDEx2(中位值:0.011%)和ANCOM-II(中位值:0.029%)的类似趋势也很明显。

最后，我们还检查了过滤后的数据集中每个工具所识别的显著ASV的判别值(discriminatory value)。通过判别值，我们指的是使用硬界限丰度值，单个ASV能够很好地描述样本组。对于该分析，我们将每一个显著ASV输入的相对丰度或CLR丰度用于预测目标组的ROC曲线。使用原始丰度值作为输入，并选择多个最佳截止点以产生ROC，比较敏感性与特异性。然后，我们测量了每种显著ASV的曲线下面积(AUC)，并计算了每种工具识别的所有ASV的平均值。我们发现，在使用相对丰度和CLR丰度作为输入的所有测试数据集中，通过ALDEx2或ANCOM-II鉴定的ASV的平均AUROC最高。尽管存在这种趋势，但也存在这样的情况，即尽管其他工具对于它们所识别的ASV达到了相对较高的平均AUROCs，但这些工具未能识别出任何显著ASV的ASV。例如，在human-IBD数据集中，有几个工具使用CLR或相对丰度作为输入，找到了它们所识别的ASV的平均AUROCs范围在0.8–0.9之间，而ALDEx2和ANCOM-II均未能识别出任何显著的ASV。

由于上述分析可能会惩罚那些要求较高数量的ASV但是其判别值却较低的工具，因此我们还研究了所测试的DA方法识别高于特定AUC阈值的ASV的能力。本分析的一个重要假设是，要接受准确的性能值，高于和低于所选AUROC阈值的所有ASV必须分别为真阳性和假阳性。尽管这一严格假设几乎肯定是错误的，但高于和低于AUC阈值的ASV很可能至少分别富集了真阳性和假阳性。我们发现，在AUROC阈值为0.7时，ANCOM-II和ALDEx2对两种相对丰度的精度都最高(中位值：0.99；SD：0.36，中位值：0.82，SD：0.39)和CLR数据(中位值：1.0；SD：0.35，中位值：0.83，SD：0.35)。然而，根据相对丰度(中位值：0.17和0.02)和基于CLR(中位值：0.06和0.01)的丰度，与LEfSe和edgeR等工具的相对丰度(中位值：0.96和0.69)和CLR数据(中位值：0.50和0.34)相比，他们的召回值较低。将CLR数据作为输入进行检查时，我们发现limma voom (TMMwsp)的F1评分最高(中位值：0.47)，仅次于Wilcoxon (CLR)检验(平均值：0.70)。在AUC阈值为较高的0.9时检查数据显示，除了一些工具(如ANCOM-II、corncob和CLR数据的t-test(rare))之外，所有工具的召回分数都相对较高(中位数：0.5、0.5和0.20)。在相对丰度(范围：0–0.01)和CLR数据(范围：0–0.2)方面，所有工具在此阈值下的精度评分均较低。这一结果并不奇怪，因为在实践中，我们希望DA工具能够识别出低于0.9 AUC鉴别阈值的特征。

重叠显著ASV的高度可变性

接下来，我们研究了每个数据集中不同工具之间显著的ASV重叠。 这些分析有助于深入了解解读的相似性如何取决于所应用的DA方法。我们假设，产生与其他DA工具的输出高度交叉的显著ASV的工具是最准确的方法。相反，如果具有相似方法的工具产生了相似组的显著ASV，并最终识别出都是虚假的ASV，则可能不是这种情况。无论哪种方式，跨方法识别重叠的显著ASV都可以洞察它们的可比性。

基于未过滤的数据，我们发现limma voom方法识别出了与大多数其他工具都不同的显著ASV(图3a)。然而，我们还发现，根据Wilcoxon (CLR)方法，limma voom方法确定的许多ASV也被确定为显著，尽管这些是方法学上高度不同的工具。此外，两种Wilcoxon检验方法具有高度不同的一致性特征，这突出了CLR转换对下游结果的影响。相比之下，我们发现两种MaAsLin2方法具有相似的一致性特征，尽管非稀疏方法发现的特征排名略低。我们还发现，最保守的工具ALDEx2和ANCOM-II主要确定了几乎所有其他方法也确定的特征。相比之下，edgeR和LEfSe这两种经常识别出最显著的ASV的工具，输出的未被任何其他工具识别出的ASV百分比最高:分别为11.4%和9.6%。corncob、metagenomeSeq和DESeq2在更中间的一致性特征下鉴定出ASV。

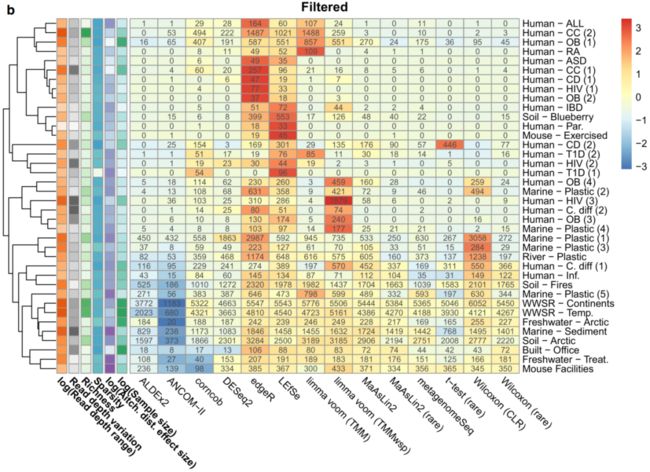
图3 跨工具和工具聚类的显著ASV特征的重叠

A,B 对于A未过滤数据和B 10%流行率过滤数据，按每个工具所调用的特征分层的，称每个特征为显著的工具数量。结果以每种工具识别的所有ASV的百分比显示。每个工具识别的显著ASV特征的总数由条形颜色表示。例如，基于未过滤的数据，这些条形图表明，ALDEx2确定的显著ASVASV中有近40%被所有其他工具共享，而ALDEx2未确定任何由少于8个工具共享的显著ASVASV。请注意，在解释这些结果时，它们取决于所包含的方法，以及是否多次表示这些结果。例如，包含两种不同的工作流来运行MaAslin2，这两种工作流产生了相似的输出；

C,D 显示了C非流行率过滤和D 10%流行率过滤数据的前两个主要坐标(PCs)的图。这些图基于我们分析的38个主要数据集的平均工具间Jaccard距离，计算方法是对所有单个数据集的工具间距离矩阵求平均值，以平均加权每个数据集。缩写:prev., previous；TMM，M值的修剪平均值(trimmed mean of M-values)；TMMwsp，具有单例配对的M值的修剪平均值(trimmed mean of M-values with singleton pairing)；rare，rarefied；CLR，center-log-ratio。源数据以源数据文件的形式提供。

基于流行率过滤数据的显著ASV重叠总体上与未过滤数据结果相似(图3b)。一个重要的不同是，与未过滤的数据相比，limma voom方法识别出的ASV在大多数其他工具中也识别出的比例要高得多。尽管如此，与未过滤的数据结果相似，Wilcoxon (CLR)显著的ASV表现出双峰分布，与limma voom方法高度重叠。我们还发现，总体而言，被12种以上工具一致认定为显著的ASV的比例在筛选数据中要高得多(平均：38.6%；SD: 15.8%)，与未过滤数据比较(平均值：17.3%；SD: 22.1%)。与未过滤的结果相反，corncob、metagenomeSeq和DESeq2的ASV比例较低，处于中间一致性等级。然而，ALDEx2和ANCOM-II再次产生了与大多数其他工具基本重叠的显著ASV。

上述分析的一个主要警告(caveat)是，每个DA工具产生的ASV总数不同。因此，原则上，所有工具都可以识别相同的顶级ASV，并且在识别不太明显的差异ASV时，只需承担不同程度的风险。为了研究这种可能性，我们确定了每个数据集排名前20位的ASV之间的重叠，在某些情况下包括非显著(但排名相对较高)的ASV。这些ASV在所有工具的20个顶级点击量中的分布与上述所有显著ASVASV的分布相似。例如，在筛选的数据中我们发现，t检验(rare)(平均值：6.2；SD: 3.8)，edgeR，(平均：6.5；SD: 4.6)，corncob(平均：6.0；SD: 4.1)，metagenomeSeq(平均：5.2；SD: 4.7)和DESeq2(平均：4.7；SD: 4.5)的ASV数量最多，仅被该特定工具确定为位于前20名。平均而言，在过滤(平均值：0.21；SD: 0.62)和未过滤(平均值：0.11；SD: 0.31)的数据集中，只有少数ASV在所有工具中排名前20。上述分析总结了工具输出的一致性，但仅从这些结果中很难辨别哪些工具表现最相似。为了确定总体上表现相似的工具，我们基于显著ASV集合之间的Jaccard距离进行了主坐标分析(图3c，d)。这些分析提供了对不同工具的结果预期有多相似的洞察，这可能是由于它们之间在方法上的相似性。然而，这并不能为哪种工具最准确提供明确的证据。未过滤和过滤数据的一个明显趋势是，edgeR和LEfSe聚集在一起，而且在第一个主坐标上与其他方法分离。有趣的是，corncob，这是一个独特的方法，在第一个主坐标上也与这两种方法聚类相对接近。这可能反映出，当考虑到通常与微生物组数据相关的参数值时，这两种方法所依赖的分布变得相似。

第二个主坐标上的主要异常值因数据是否经过流行率过滤而不同。对于未过滤的数据，主要的异常值是limma voom方法，其次是Wilcoxon(CLR；图3c)。相反，在第二主坐标上，ANCOM-II是基于过滤数据的唯一的主要异常值(图3d)。这些可视化突出了基于所产生的显著ASV集合的主要工具的簇。然而，在每种情况下，由前两个组成部分解释的变化百分比相对较低，这意味着这些面板中缺少关于潜在工具聚类的大量信息。例如，ANCOM-II和corncob分别是未过滤数据分析的第三和第四主坐标上的主要异常值，这突出了这些方法的独特性。

微生物组差异丰度工具的错误发现率取决于数据集

接下来，我们评估了DA工具在预期无显著命中的情况下的表现。这些病例对应于上述38个数据集中8个数据集的子样本。对于每个数据集，我们选择了最频繁采样的组，并在此样本组内随机将它们重新分配为病例样本或对照样本。然后对随机分配的样本子集运行每个DA工具，并比较结果。由于分配的随机性质以及来自相同元数据分组的样本的相似组成(例如，健康人类)，我们预期工具不会将任何ASV识别为具有显著差异的丰度。通过这种方法，我们能够推断出每种工具的假阳性特征。换句话说，即使样本组之间没有预期的差异，我们也确定了每种工具所称的受试ASV的显著百分比。

未过滤和过滤数据最明显的趋势是，在这种情况下，某些异常值工具的FDR相对较高，而大多数其他工具识别的假阳性很少(图4)。两种limma voom方法输出的显著ASV百分比差异很大，尤其是基于未过滤的数据(图4a)。在5/8的未过滤数据集中，由于许多高值异常值，limma voom方法平均确定了超过5%的ASV为显著。在未过滤数据分析中，只有ALDEx2和t-test(rare)一致认定无ASV存在显著差异。然而，在大多数测试数据集(分别为6/8和7/8)中，MaAsLin2和Wilcoxon(rare)均未发现显著特征。筛选数据分析中的两个明显异常值是edgeR(平均值：0.69–27.9%)和LEfSe(平均值：3.4–5.1%)，这两个异常值与其他工具相比一致地识别出更显著的命中(图4b)。然而，应该注意的是，在一些数据集上，corncob、DESeq2法和limma法也表现不佳。

图4 未过滤和过滤数据的错误发现率模拟重复的分布

显示了每个单独数据集和工具对p值进行Benjamin I-Hochberg校正(使用0.05的界限值)后显著的扩增子序列变异的百分比。箱线图的四分位数间范围(IQR)代表第25和75个百分位数，而最大值和最小值代表1.5倍IQR以外的最大值和最小值。箱线图中间的凹口代表中位值。请注意，x轴的刻度为伪log10。a代表未筛选的数据集，b代表使用每种ASV 10%的流行率要求筛选的数据集。数据集和工具运行100次，同时将来自相同环境和原始分组的样本随机分配到两个新的随机选择分组中的一个。然后对两个随机分组进行差异丰度分析。请注意，在未筛选的数据集内，8个数据集(淡水-北极、土壤-蓝莓、人类-OB(1))中仅运行了3个数据集的100个重复项，在Human - HIV (3)数据集中也运行了100个ALDEx2重复项。由于计算方面的限制，所有其他未筛选的数据集都进行了10次重复运行。缩写:prev., previous；TMM，M值的修剪平均值(trimmed mean of M-values)；TMMwsp，具有单例配对的M值的修剪平均值(trimmed mean of M-values with singleton pairing)；rare，稀有(rarefied)；CLR，中心对数比(center-log-ratio)。源数据以源数据文件的形式提供。

总体而言，我们发现过滤后的数据集中显著的ASV的原始数量低于未过滤数据中的原始数量(正如预期的那样，因为许多ASV被过滤掉)，并且无论采用何种过滤程序，大多数工具仅识别出一小部分显著的ASV。两种limma voom方法除外，这两种方法对未过滤数据的FDR较高，edgeR和LEfSe对过滤数据的FDR较高。尽管这些工具的平均表现非常突出，但我们还观察到，在对未过滤数据集进行的多次重复中，Wilcoxon (CLR)方法将几乎所有特征确定为具有统计学意义(图4a)。两种limma voom方法也是如此，这突出表明少数重复项推高了这些方法的平均FDR。

我们对Wilcoxon (CLR)方法的异常值重复进行了研究，发现在30%或以上的ASV具有显著性的重复中，两个受试组之间的平均read深度差异始终较高。这些差异与试验组之间每个样本的几何平均丰度(即CLR变换的分母)的类似差异有关。具体而言，就每个数据集而言，这些异常值重复通常显示了测试组之间几何平均值的最极端平均值差异，并且在其他方面也位于十大最极端重复之列。有趣的是，当检查limma voom方法的异常值重复时，差异read深度模式不存在。

不同腹泻病例对照数据集的工具不尽相同

除了上述比较同一数据集中不同工具之间一致性的分析之外，我们接下来研究了某些工具是否能在同一疾病的不同数据集之间提供更一致的信号。该分析集中于跨工具的属水平，以帮助限制研究间的差异。我们特别关注作为表型的腹泻，研究显示腹泻对微生物组有很强的影响，并且在各项研究中具有相对的可重复性。

我们为本分析采集了五个数据集，分别代表腹泻个体与非腹泻个体的微生物组。我们对每个单独的过滤数据集运行了所有DA工具，并将我们的分析限制在所有数据集内发现的218个属。与我们的ASV水平分析一样，这些工具在所识别的显著属的数量方面存在显著差异。例如，ALDEx2确定每个数据集中的平均值为17.6个显著属(SD: 17.4)，而edgeR确定的平均值为46.0个显著属(SD: 12.9)。因此，与具有较少显著命中的工具相比，通常将更多属识别为显著的工具更可能将属识别为一致显著。因此，工具间比较每个属被确定为显著的次数不能再提供信息。

相反，在给定随机数据的情况下，我们分析了每个属被确定为显著的研究数量的观测分布与预期分布。这种方法使我们能够根据每种工具相对于其自身随机预期的一致程度来比较这些工具。例如，平均而言，与ALDEx2相比，edgeR在各研究中更一致地确定了显著的属(edgeR和ALDEx2在各研究中发现的属的数据集平均数分别为1.67和1.54)。然而，这一观察结果仅仅是由edgeR鉴定的显著属的数量增加所驱动的。实际上，与随机预期相比，ALDEx2在对观测数据中的显著属进行调用时显示出1.35倍的一致性增加(p < 0.001)。相比之下，edgeR得出的结果与随机预期相比仅一致1.10倍(p = 0.002)。

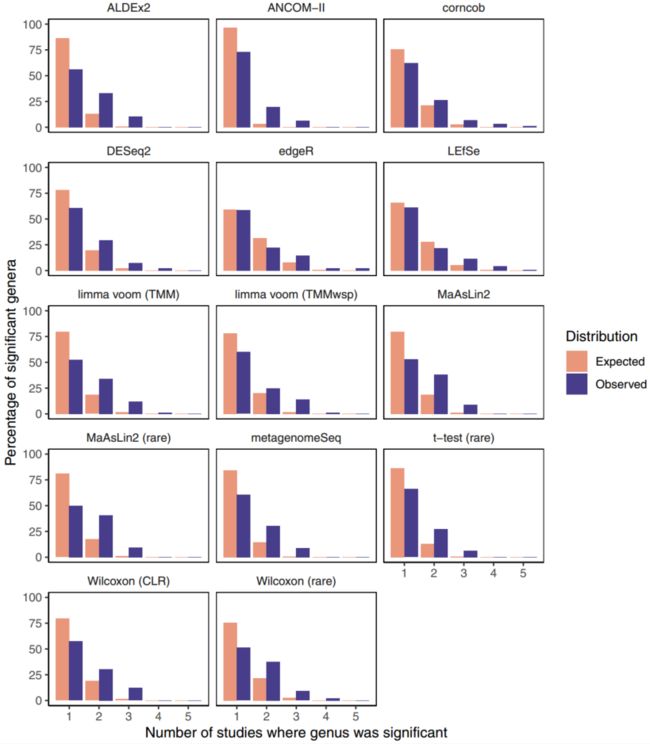
ALDEx2和edgeR代表了工具在不同研究中如何一致地将同一属识别为显著的极端情况，但它们的范围很大(图5)。值得注意的是，所有工具在这些数据集上的一致性显著高于随机预期(p < 0.05)(表2)。除了ALDEx2之外，基于该评估的其他表现最佳的方法包括limma voom (TMM)、MaAsLin2工作流和ANCOM-II。

图5 腹泻数据集中显著属的观测一致性总体高于随机预期

这些条形图说明了每个属被确定为显著的研究数量的分布(不包括从未发现具有显著意义的属)。随机期望分布是基于重复随机选择属作为显著性，然后计算跨研究的一致性。缩写:prev., previous；TMM，M值的修剪平均值(trimmed mean of M-values)；TMMwsp，具有单例配对的M值的修剪平均值(trimmed mean of M-values with singleton pairing)；rare，稀有(rarefied)；CLR，中心对数比(center-log-ratio)。源数据以源数据文件的形式提供。

表2 五个腹泻数据集中差异丰度属的观察和预期一致性比较

No. sig. genera:在至少一个数据集中显著的属的数量；Max overlap: 该工具称属为显著的数据集的最大数量；Mean exp.: 每个属预计具有显著意义的数据集的平均数量(在至少一次具有显著意义的属中)；Mean obs.:每个属被观察到具有显著意义的数据集的平均数量(在至少一次具有显著意义的属中)；Fold diff.:在多个数据集上观察到的平均显著属数高于平均预期显著属数的倍差；p:基于使用“平均观测值”作为检验统计量的单尾置换检验的p值。注意用<0.001 表示，而不是精确值，因为 0.001 是我们可以根据置换方法估计的最小非零 p 值。源数据被提供为源数据文件。

我们在五个肥胖16S rRNA基因数据集上进行了类似研究，由于总体一致性较低，解释起来更具挑战性。具体而言，仅在一项研究中调用了最显著的属，且仅MaAslin2(均有非稀释和稀释数据)、t检验(rare)方法、ALDEx2和limma voom (TMMwsp)方法的表现明显好于偶然预期(p < 0.05)。基于这些数据集，MaAsLin2(rare)方法产生了迄今为止最一致的结果(倍差：1.23；p = 0.003)。

讨论

在此，我们比较了常用DA工具在16S rRNA基因数据集上的性能。虽然有人可能会认为，由于工具测试不同的假设，预期工具输出会有差异，但我们认为，这种观点忽视了这些工具在实践中是如何使用的。特别是，这些工具在微生物组文献中经常被交替使用。因此，提高对DA方法性能变化的理解对于正确解释微生物组研究至关重要。我们在此举例说明，这些工具可能产生实质上不同的结果，这强调了基于微生物组数据分析的许多生物学解释可能对DA工具的选择不具稳健性。这些结果可能部分解释了一个常见观察结果，即一个数据集中报告的重要微生物特征与相似数据集中的重要结果仅略微重叠。然而，应注意，这也可能是由于影响微生物组研究的许多其他偏见造成的。我们的发现应作为研究者进行自身微生物组数据分析的警示，并强调需要准确报告一组具有代表性的不同分析方案的发现，以确保报告稳健的结果。重要的是，读者不应将我们的结果误解为16S rRNA基因数据的可靠性低于其他微生物组数据类型，如shotgun宏基因组学和代谢组学。我们预计类似的问题会影响这些数据类型的分析，因为它们具有相似甚至更高的稀疏性和样本间差异。尽管如此，尽管不同DA工具的结果存在较大差异，但我们能够确定各种工具产生的几种一致模式的特征，研究人员在评估自己的结果和已发表工作的结果时应牢记这些模式。

DA工具的两个主要组可以通过它们倾向于识别多少显著ASV的ASV来区分。我们发现，limma voom、edgeR、Wilcoxon (CLR)和LEfSe平均产生大量显著的ASV。相比之下，ALDEx2和ANCOM-II倾向于仅确定相对少数的ASV为显著。我们假设后一种工具更保守，精确度更高，但伴随敏感性的可能损失。该假设与我们的观察结果相关，即通过这两种工具识别的显著ASV也往往通过几乎所有其他差异丰度方法识别，我们将其解释为更可能为真阳性的ASV。此外，很明显，在大多数情况下，但不是所有情况下，这两种方法都倾向于识别其他工具发现的最具歧视性的反车辆地雷。我们认为，这些方法确定的ASV数量较低可能是多种原因造成的。ALDEx2的保守性质很可能是由于其Monte Carlo Dirichlet采样方法，该方法降低了低丰度ASV的权重。另一方面，ANCOM-II的保守性可归因于其巨大的多重检测负担。此外，所识别的特征数量的差异也可能归因于一些工具用于移除潜在ASV进行测试的预处理步骤。这包括未报告仅在一个组中发现的ASV的显著性值的corncob或ANCOM-II去除结构零的能力。虽然不清楚为什么有些方法的显著性比其他工具高得多，但可能有几个原因。其中包括LEfSe选择不校正虚假发现的显著性值，或Wilcoxon (CLR)无法考虑元数据分组之间的测序深度差异。需要注意的是，在某些情况下，当不包括子类时，作者没有选择将FDR p值校正应用于LEfSe输出，但是，这不是该工具的默认行为。

鉴于使用多种方法通常被确定为显著的ASV可能更可靠，值得注意的是，未过滤数据中的显著ASV往往被更少的工具识别。这在limma voom方法和Wilcoxon (CLR)方法中尤为明显。尽管许多显著ASV的ASV可能会被其他工具错误地忽略，但更有可能的是，由于数据稀疏等多种原因，这些工具在未过滤数据上的表现尤其糟糕。

limma voom方法的这一问题也因几个未经过滤的随机数据集的高假阳性率而得到强调，这与FDR过去对这一方法的评估一致。我们认为，这个问题很可能是由TMM规范化方法无法处理高度稀疏的数据集所驱动的，因为过滤数据会使性能更接近其他DA方法。重要的是要承认，我们用于估计FDR的随机方法并不能完美地代表真实数据；也就是说，真实的样本分组可能包含微生物丰度的一些系统差异——尽管影响大小可能非常小——而我们的随机数据集应该没有。因此，根据这种方法仅确定少数显著ASV的ASV并不一定证明工具在实践中具有低的FDR。然而，在缺乏可区分信号的情况下识别许多显著ASV的工具也可能对实际数据具有较高的FDR。

基于该分析的另外两个有问题的工具是edgeR和LEfSe。以前曾多次发现edgeR方法表现出较高的FDR。尽管metagenomeSeq也被标记出现了这种情况，但在我们的分析中并未出现这种情况。这与最近的一份报告一致，即metagenomeSeq(使用零膨胀对数正态方法(zero-inflated log-normal approach)，正如我们所做的)适当控制了FDR，但表现出较低的功率(power)。关于ANCOM是否适当控制FDR，以前的结果喜忧参半，但我们有限分析的结果表明，这种方法是保守的，控制了FDR，但有时可能会遗漏真正的阳性结果，这在我们的判别分析中很明显。

与此相关，我们发现，在5个腹泻相关数据集上，ANCOM-II在将相同属鉴定为显著DA方面表现优于平均水平，尽管每个数据集仅将4个属的平均值鉴定为显著。尽管如此，ANCOM-II的结果不如ALDEx2、MaAsLin2工作流和limma voom (TMM)一致。跨数据集产生最不一致结果的工具(相对于随机预期)包括t-test(rare)方法、LEfSe和edgeR。在这种情况下，随机预期是非常简单的；它是基于所有属都同样可能是偶然重要的假设而产生的。这个假设一定在某种程度上是无效的，因为在样本中某些属比其他属更普遍。因此，令人惊讶的是，这些工具只产生了比预期稍微更一致的结果。

尽管这种跨数据一致性分析提供了大量信息，但值得注意的是，并非所有环境和数据集都适合进行这种比较。具体而言，我们发现五个数据集之间的显著属的一致性比较肥胖个体和对照个体并不比大多数工具的偶然预期高。这一观察结果不一定反映出肥胖和非肥胖个体之间几乎没有一致的属差异；相反，它可以简单地反映我们所分析的特定数据集之间存在差异的技术和/或生物因素1。尽管存在这些复杂因素，但值得注意的是，基于这些数据集，MaAsLin2工作流和ALDEx2产生的结果比预期的更一致。

我们认为上述关于DA工具的观察很有价值，但许多读者可能主要感兴趣的是听到具体的建议。事实上，微生物组分析中对标准化实践的需求最近得到了更好的理解。我们工作的一个目标是验证另一份最近的DA方法评估报告中的建议，该报告发现limma voom、corncob和DESeq2在他们测试的工具中表现最好。基于我们的结果，我们不建议将这些工具作为数据分析的唯一方法，相反，我们建议研究人员使用更保守的方法，如ALDEx2和ANCOM-II。尽管这些方法的统计能力较低，但考虑到将假阳性识别为差异丰富的成本较高，我们认为这是一个可接受的权衡。然而，对于希望以更多假阳性为潜在代价获得更高统计能力的用户来说，MaAsLin2(尤其是对于经过稀释的数据)也是一个合理的选择。我们可以明确建议用户避免使用edgeR(一种主要用于RNA-seq数据的工具)和LEfSe(不进行p值校正)对16S rRNA基因数据进行DA检测。 用户还应注意，limma voom和Wilcoxon (CLR)方法在处理高度稀疏的未过滤数据时可能表现不佳。对于Wilcoxon (CLR)方法来说，当感兴趣的组之间的测序深度有很大差异时尤其如此。

更一般地说，我们建议用户采用多种方法，并关注大多数工具所识别的显著特征，同时牢记本手稿中介绍的工具的特征。例如，作者可能希望根据本文中提供的工具特征或一致认可其识别的工具数量，按类别提供已识别的分类标记。重要的是，对同一数据集应用多个DA工具时，应明确报告。显然，这种方法会使结果更难从生物学角度解释，但它会提供一个更清晰的视角，说明哪些差异丰富的特征对分析中的合理变化是稳健的。

在DA工具中使用共识方法的一个常见的反论点是，不能保证工具输出的交集更可靠；这些工具可能只是拾取了与显著相同的噪声。尽管我们认为这不太可能，但无论如何，运行多个DA工具对于为报告显著功能提供背景仍然很重要。例如，与其他DA方法相比，研究人员可能正在使用一种产生高度不重叠的显著特征集的工具。即使研究人员对他们的方法有信心，这些差异也应该在结果汇总时弄清楚。这对于准确洞察通常使用不同DA方法的独立研究中的特定发现的稳健性至关重要。同样，如果研究人员最感兴趣的是确定某项特定研究的信号是否可再现，那么他们应确保使用相同的DA方法，以提高结果的可比性。

在进行DA检测之前，如何以及是否要对数据进行独立过滤，是有关微生物组数据分析的其他重要未决问题。 尽管关于独立过滤有效性的统计论证超出了本文的范围，但从直觉上讲，排除仅在少数样本中发现的特征是合理的(无论这些样本属于哪一组)。其基本原因是，否则多重测试校正的负担会变得如此之大，以至于几乎禁止识别任何差异丰富的特征。尽管存在这一缺陷，但许多工具在未过滤的数据中发现了大量显著的ASV。然而，在未过滤的数据中，这些显著的ASV往往更具工具特异性，不同工具间显著的ASV百分比差异更大。因此，我们建议在DA检测之前对特征进行流行率(prevalence)过滤(例如，10%)，尽管我们承认需要做更多的工作来估计最佳界限，而不仅仅是任意选择一个界限。

另一个常见问题是，是否应避免使用要求输入经过稀释的的DA工具。是否对数据进行稀释的问题可能在微生物领域受到了过多的关注：还有许多其他因素会影响分析管道，这些因素可能会对结果产生更大的影响。事实上，在我们的分析中，采用稀释后的数据的工具的平均表现并不比其他方法差多少。更具体地说，最一致的工具间方法ANCOM-II和ALDEx2基于非稀疏数据，但基于稀疏数据的MaAsLin2在相同表型的数据集上产生最一致的结果。因此，我们不能肯定地得出结论，认为需要对输入数据进行细化的DA工具总体上不太可靠。值得注意的是，我们仅在DA测试的背景下提及稀释：稀释是否适合其他分析，如在计算多样性指标之前，不在本工作的范围内。

其他人通过将模拟应用于各种DA方法来研究上述问题，并得出了有价值的见解。但是，我们认为这并不能全面反映这些DA工具的性能。这是因为有人强调，在许多情况下，模拟可能会导致循环论证，即围绕特定参数设计的工具在使用这些参数的模拟中表现良好。如果不更好地了解微生物组测序可能导致的数据结构范围，这些类型的模拟分析可能难以解释。因此，我们认为，在大量不同的现实世界数据集上测试这些方法很重要，以便了解它们之间的差异。通过这样做，我们在文献中强调了可互换使用这些工具的问题。实际上，问题是“哪些分类群在样本分组之间的相对丰度有显著差异？”可能太简单，需要进一步的参数化才能回答。这包括诸如作者正在比较的丰度类型以及他们计划在分析中使用的工具等信息。不幸的是，工具之间的差异意味着基于这些问题的生物学解释通常会因所考虑的DA工具而有很大差异。

总之，在众多16S rRNA基因测序数据集上，DA工具输出的高度变异凸显了微生物组研究人员面临的一个令人担忧的再现性危机。虽然我们不能根据分析结果对特定工具提出直接简单的建议，但我们强调了作者在解释DA结果时应注意的几个问题。这包括edgeR和LEfSe等几种工具的错误发现率过高，因此应尽可能避免使用。从我们的分析中也可以清楚地看出，一些为RNA-seq设计的工具，如limma voom方法，如果不包括数据过滤步骤，就无法处理微生物组数据的高度稀疏性。我们还强调了这些工具在它们认为显著不同的ASV数量上可能存在显著差异，并且一些工具在数据集之间比其他工具更一致。总的来说，我们建议作者在比较特定研究之间的结果时使用相同的工具，或者使用基于几种DA工具的共识方法，以帮助确保结果对DA选择是稳健的。

方法

数据集处理

我们的主要分析包括38个不同的数据集，用于评估微生物组差异丰度工具的特征。还纳入了另外三个数据集，以比较腹泻和肥胖相关微生物组数据集之间的差异丰度一致性。本文提供的所有数据集均已在之前发表过或公开提供。大部分数据集已经以表格形式提供，具有ASV或OTU，而少数数据集需要从原始序列进行处理。这些原始序列根据QIIME 2 2019.7版的微生物组辅助标准操作程序(Microbiome Helper standard operating procedure)进行处理。使用cutadapt移除引物，并使用QIIME 2 VSEARCH连接对(join-pairs)插件拼接在一起。然后使用质量过滤(quality-filte)插件对拼接后的reads进行质量过滤，并使用Deblur对reads进行去噪，以产生扩增子序列变体(ASV)。然后，每个样本的ASV丰度表被输出到制表符分隔的文件中。还为每个数据集生成了稀疏表，其中稀疏read深度(rarefied read depth)被取为数据集内超过2000条reads的任何样本的最低read深度(丢弃低于此阈值的样本)。

使用在VSEARCH (v2.17.1) 中实施的UCHIME2和UCHIME3嵌合体检查算法识别嵌合ASV。除了基于UCHIME2参考的嵌合体检查方法外，还应用了UCHIME2和UCHIME3 de novo 方法。对于后一种方法，我们使用了SILVA v138.1短亚基(short-subunit)参考数据库。我们在运行这些算法时使用了默认选项。

差异丰度检验

我们创建了一个自定义shell脚本(run_all_tools.sh)，在本研究的每个数据集上运行每个差异丰度工具。作为输入，该脚本采用了一个制表符分隔的ASV丰度表、该表的精简版本以及一个元数据文件，该文件包含一个将样本分成两组进行测试的列。该脚本还接受了流行率(prevalence)截止过滤器，以去除低于最小截止值的ASV，对于我们呈现的过滤数据分析，该最小截止值被设定为10%(即，在不到10%的样本中发现的ASV被去除)。请注意，在少数情况下，输入的是属丰度表，在这种情况下，所有选项都保持不变。当设置了流行过滤器选项时，脚本还基于输入稀疏深度生成新的过滤稀疏表。

按照这些步骤，我们根据不同工具的推荐，使用稀释后的或未经稀释的表格运行每个单独的差异丰度方法。使用GUniFrac(1.1版)进行稀释。用于运行每个差异丰度工具(使用run_all_tools.sh)的工作流程描述如下。每个工作流的第一步是用自定义脚本将数据集表读入R(3.6.3版)，然后确保元数据和丰度表中的样本顺序相同。选择α值0.05作为我们的显著性界限，将FDR调整后的p值(使用Benjamini-Hochberg调整)用于输出p值的方法(LEfSe除外，默认情况下，它不输出所有p值)。

ALDEx2

我们将未经稀释的特征表和相应的样本元数据传递给来自ALDEx2 R包(1.18.0版)的aldex函数，该包使用统一先验为每个样本生成Dirichlet分布的Monte Carlo样本，对每个实现执行CLR变换，然后对变换后的实现执行Wilcoxon测试。然后，该函数基于不同Monte Carlo的结果，返回每个特征的预期Benjamini-Hochberg (BH) FDR校正p值。

ANCOM-II

我们通过R ANCOM-II(https://github.com/FrederickHuangLin/ANCOM)(2.1版)**feature_table_pre_process函数运行未经稀释的特征表**，该函数首先检查丰度表以识别异常值零(outlier zeros)和结构零(structural zeros)。ANCOM-II导入了以下软件包：exactRankTests(版本0.8.31)、nlme(版本3.1.149)、dplyr(版本0.8.5)、ggplot2(版本3.3.0)和compositions(版本1.40.2)。异常值零是通过在每个样本分组内的分类单元计数分布中发现异常值而确定的，在差异丰度分析期间被忽略，代之以NA。在数据分析期间，忽略了结构零(一个分组中不存在但另一个分组中存在的分类单元)，并自动将其称为差异地丰富。然后对整个数据集应用伪计数1，以允许log转换。使用主函数ANCOM，然后使用Wilcoxon秩和检验对每个分类单元的所有加性log比进行显著性检验，并使用BH方法对p值进行FDR校正。然后，ANCOM-II应用如原始论文中所述的检测阈值，据此，如果某个分类单元达到标称显著性的校正p值数量大于最大可能显著性比较数量的90%，则该分类单元被称为DA。

corncob

我们将元数据和未经稀释的特征表转换为phyloseq对象(版本1.29.0)，并将其输入到corncob的differentialTest函数(版本0.1.0)中。该函数使每个分类单元的计数丰度符合β-二项式模型，对平均值和超方差使用logit link函数。因为corncob同时对每一种模式进行建模，并同时进行差异丰度和差异可变性测试，所以我们将空超方差模型(null over- dispersion model)设置为与非零模型(non-null model)相同，以便仅识别出具有差异丰度的分类群。最后，该函数进行了显著性检验，为此我们选择了Wald检验(使用默认的非自举设置)，并获得了BH FDR校正的p值作为输出。

DESeq2

我们首先将未经稀释的特征表传递给带有默认设置的DESeq函数(版本1.26.0)，除了将大小因子的估计设置为使用“poscounts”而不是默认的相对log表达式(也称为比值中位法)之外，该表达式计算修改后的相对log表达式，以帮助解释至少一个样本中缺失的特征。该函数执行三个步骤：(1)大小因子（size factors）的估计，其用于以基于模型的方式标准化测序文库大小；(2)从每个特征的负二项式似然估计离差，并且随后通过经验贝叶斯将每个离差估计收缩到参数(默认)趋势线；(3)用负二项广义线性模型将每个特征拟合到指定的类分组，并执行假设检验，对此我们选择了默认的Wald检验。最后，使用结果函数，我们获得了经过BH FDR校正的p值。

edgeR

使用phyloseq_to_edgeR函数(https://joey711.github.io/phyloseeq-extensions/edgeR.html)，我们向**未经稀释的特征表添加了伪计数1**，并使用edge R包(版本3.28.1)中的函数calcNormFactors来计算相对log表达式规范化因子。然后使用函数estimateCommonDisp和函数estimateTagwiseDisp估计负二项式离差参数，通过经验贝叶斯方法缩小特征离差估计。然后，我们对负二项式数据使用exactTest来确定指定组之间的差异特征。然后，使用带有函数topTags的BH方法对所得到的p值进行校正，以进行多次测试。

LEfSe

首先使用LEfSe脚本format_input.py将稀释后的表格转换为LEfSe格式。然后，我们使用run_lefse.py脚本在格式化的表上运行LEfSe，该脚本带有默认设置，没有子类规范。简而言之，该命令首先使用总和缩放对数据进行归一化，将每个要素计数除以总库大小。然后进行Kruskal-Wallis(在我们的两组病例中简化为Wilcoxon秩和)假设检验，以识别潜在的差异丰富特征，随后对丰度的类标签进行线性判别分析(LDA)，以估计显著特征的影响大小。从这些特征中，只有那些定标(scaled)LDA分析得分高于阈值得分2.0(默认)的特征被称为差异丰富。这一关键步骤是LEfSe区别于Wilcoxon检验方法的地方，后者基于我们也运行的相对丰度。此外，未对原始LEfSe输出执行多项测试校正，因为此工具仅返回显著特征高于阈值LDA评分的p值。

limma voom

我们首先使用edgeR calcNormFactors函数对未经稀释的特征表进行归一化，使用M值的修剪平均值(TMM)或带有单例配对(TMMwsp)选项的TMM。我们选择使用两种不同的归一化函数来运行该工具，因为我们发现标准的TMM归一化技术难以处理高度冗余的数据集，尽管它以前在DA测试中被证明是优先执行的。此外，edgeR包中突出显示了TMMwsp方法，作为高度稀疏数据的替代方法。在任一归一化步骤中，使用上四分位数归一化法选择单个样本作为参考样本。这一步骤在一些高度稀疏的丰度表中失败；在这些情况下，我们选择具有最大平方根变换特征丰度和的样本作为参考样本。归一化后，我们使用limma R包(3.42.2版)函数voom将归一化计数转换为每百万log2计数，并根据均值-方差趋势为每个观察结果分配精度权重。然后，我们使用limma R软件包中的函数lmFit、eBayes和topTable来拟合加权线性回归模型，基于经验Bayes调节的t-statistic执行测试，并获得BH FDR校正的p-值。

MaAsLin2

我们将一个稀释后的或未经稀释的特征表输入到MaAsLin2 R包(版本0.99.12)中的主要Maaslin2函数中。我们在包简介(而不是默认日志)和总和缩放归一化中指定了反正弦平方根变换(arcsine square-root transformation)。为了与其他工具保持一致，我们没有指定随机效应，并关闭了默认的标准化。该函数将线性模型拟合到指定样本分组上每个特征的转换丰度，使用Wald检验进行显著性检验，并输出BH FDR校正的p值。

metagenomeSeq

我们首先将计数和样本信息输入metagenomeSeq R包(1.28.2版)11中的newMRexperiment函数。接下来，我们使用cumNormStat和cumNorm应用累积和缩放归一化，试图基于特征的低四分位数丰度对序列计数进行归一化。然后，我们使用fitFeatureModel用零膨胀的对数正态模型(在log2转换之前增加伪计数1)拟合归一化特征计数，并执行经验贝叶斯调节t检验和MRfulltable，以获得BH FDR校正的p值。

t检验

我们对经过稀释的特征表应用总和缩放归一化(total sum scaling normalization)，然后对每个特征执行不成对Welch t检验，以比较指定的组。我们使用BH法校正了多次检测的p值。

Wilcoxon检验

在稀释后下使用原始特征丰度，在未经稀释情况下使用CLR转换的丰度(应用伪计数1后)，我们对每个特征执行Wilcoxon秩和检验，以比较指定的样本分组。我们用BH法校正了所得的p值。

比较工具之间的显著ASV命中数

我们比较了每种工具在38个不同数据集内识别的显著AVS的数量。如上所述，使用默认设置运行每个工具，并根据工具作者的建议进行一些修改。使用pheatmap R软件包(版本1.0.12)构建了一个热图，该热图代表了每种工具发现的显著ASV命中数。使用R中的cor.test函数计算工具识别的显著ASV百分比与下列数据集特征之间的Spearman相关性:样本大小，使用PERMANOVA检验计算的Aitchison距离效应大小(adonis；vegan，版本2.5.6)、稀疏性、平均样本ASV丰富性、中位样本read深度、样本之间的read深度范围以及数据集内read深度的变异系数。此外，对于未过滤的分析，我们还计算了每个数据集中ASV的流行率低于10%的Spearman相关性(即，将被移除以产生过滤数据集的ASV的百分比)。使用R package corrplot(版本0.85)和gridExtra(版本2.3)显示相关性。使用以下R包进行用于画图的数据操作：doMC(1.3.5版)、doParallel(1.0.15版)、matrixStats(0.56.0版)、reshape2(1.4.4版)、plur(1.8.6版)和tid yverse(1.3.0版)。

跨工具、研究内差异丰度一致性分析

我们通过汇总38个不同数据集中至少一种工具确定为显著的所有ASV，比较了所有数据集中不同工具之间的一致性。然后对鉴定每种ASV差异丰富的方法数进行计数。在不选择特定显著性阈值的情况下检查方法间一致性的第二种方法是检查每种DA方法识别的前20个ASV之间的重叠。为此，除ANCOM-II(使用其W统计量进行排序)外，根据每种DA方法的显著性值对ASV进行了排序。与上述分析一样，我们计算了将每种ASV确定为其前20种差异最大的ASV的方法数。使用R package cowplot(1.0.0版)和ggplotify(0.0.5版)组合多面板图形。为了获得数据的另一个视图，使用38个主要数据集的平均工具间Jaccard距离构建了主坐标分析图。通过对所有单个数据集的工具间距离矩阵求平均值来计算距离，以使用R packages vegan(2.5.6版)和parallelDist(0.2.4版)对每个数据集进行平均加权。标签使用R package ggrepel(0.8.1版)显示。

假阳性分析

为了评估每种DA方法的假阳性率，选择了8个来自不同环境类型的样本量最大的数据集进行分析。在每个数据集中，仅选择最频繁的样本组进行分析，以帮助确保测试样本的组成相似。在该分组中，将病例或对照的随机标签分配给样本，并对其测试了各种差异丰度方法。除了ALDEx2、ANCOM-II和corncob之外，每个数据集和工具组合都重复了100次。仅在8个数据集(淡水-北极(Freshwater – Arctic)、土壤-蓝莓(Soil – Blueberry,)、人- OB(human - OB) (1))中的3个数据集上运行了100个重复，在人- HIV(human - HIV) (3)数据集上也运行了100个ALDEx2重复。这是因为在所有数据集上运行这些工具需要很长的计算时间。其余数据集在这三种工具中各复制了10次。完成该分析后，使用每种工具鉴定的差异丰富的ASV数量按α值0.05评估。使用R软件包ggplot2(3.3.0版)、ggbeeswarm(0.6.0版)和scales(1.1.0版)构建了此数据的箱线图。

跨研究差异丰度一致性分析

对于本次分析，我们采集了另外两个未用于其他分析的预处理数据集，即GEMS1和dia_schneider数据集。这些数据集的处理数据分别来自MicrobiomeDB和microbiomeHD。这些数据集与本手稿其他地方使用的三个数据集(Human-c . diff[1和2]和Human-Inf)相结合。)，使腹泻相关数据集的数量达到5个。这三个预先存在的数据集均与肠道感染相关，之前均已证明显示患者样本中由腹泻驱动的微生物差异的独特信号。

在肥胖跨研究分析中，我们利用了核心38个数据集的四个数据集:Human-OB(1-4)。我们还纳入了从微生物学数据库中获得的另一个肥胖数据集ob_zupancic。

每个数据集中的ASV之前都进行了分类，因此我们使用这些分类将所有特征丰度折叠到属水平。请注意，分类分类是使用几种不同的方法进行的，这是技术差异的另一个来源。我们排除了未分类和严格意义上标记的属水平。然后，我们在属水平上对这些数据集运行了所有差异丰度工具。这些比较是在腹泻和非腹泻样本组之间进行的。相同的处理工作流程也用于补充肥胖数据集比较。

对于每种工具和研究组合，我们确定了在α为0.05时哪些属存在显著差异(如相关)。然后，对于每种工具，我们统计了每种属的显著性次数，即基于给定的工具，每种属在多少数据集上显著。每个工具的这些计数的零期望分布是通过从每个数据集中随机采样属而生成的。对一个属进行采样(即称其为显著)的概率被设置为等于实际显著属的比例。重复该程序1000次，属重复数等于试验属的实际数量(腹泻和肥胖数据集分别为218和116)。对于每个复制，我们计算了在数据集上对该属进行采样的次数。请注意，为了简化分析，我们忽略了显著性的方向性(例如，病例样本或对照样本中的方向性是否更高)。我们还排除了从未发现有意义的属。我们计算了这1000个分布的平均值，以生成研究预期平均数的经验分布，其中给定随机抽样，一个属将被称为显著。我们确定了每个相应分布的观测平均值，以计算统计显著性。

判别分析

我们基于每种ASV的受体算子曲线(ROC)的曲线下面积(AUC)，计算了该ASV的判别值(即ASV可用于区分样本组的程度)。这是对非稀薄相对丰度和CLR丰度独立进行的。对于数据集中的每个ASV，该ASV的丰度连同元数据分组被用作ROCR R包中预测函数的输入。然后使用多个不同的最佳丰度界限，根据输入的ASV丰度对样本进行分类。然后将分类与真实样本分组进行比较，以生成38个测试数据集内每种ASV的ROC。对于每种工具，分别基于相对丰度和CLR丰度，计算了每个数据集中被确定为差异丰富的所有ASV的平均AUC。然后，当使用0.7或0.9的AUC界限值时，我们计算了测试数据集的每种工具的精确度、召回率和F1评分。在每种情况下，“真阳性”都被视为高于指定AUC阈值的特征。

编译：吴季秋

责编：马腾飞 南京农业大学

审核：刘永鑫 中科院遗传发育所

Reference

Jacob T. Nearing, Gavin M. Douglas, Molly G. Hayes, Jocelyn MacDonald, Dhwani K. Desai, Nicole Allward, Casey M. A. Jones, Robyn J. Wright, Akhilesh S. Dhanani, André M. Comeau, Morgan G. I. Langille. Microbiome differential abundance methods produce different results across 38 datasets. Nature Communications 13:342, (2022) https://doi.org/10.1038/s41467-022-28034-z

猜你喜欢

iMeta简介 高引文章 高颜值绘图imageGP 网络分析iNAP
iMeta网页工具 代谢组MetOrigin 美吉云乳酸化预测DeepKla
iMeta综述 肠菌菌群 植物菌群 口腔菌群 蛋白质结构预测

10000+：菌群分析 宝宝与猫狗 梅毒狂想曲 提DNA发Nature

系列教程：微生物组入门 Biostar 微生物组  宏基因组

专业技能：学术图表 高分文章 生信宝典 不可或缺的人

一文读懂：宏基因组 寄生虫益处 进化树 必备技能：提问 搜索  Endnote

扩增子分析：图表解读 分析流程 统计绘图

生物科普:  肠道细菌 人体上的生命 生命大跃进  细胞暗战 人体奥秘  

写在后面

为鼓励读者交流快速解决科研困难，我们建立了“宏基因组”讨论群，己有国内外6000+ 科研人员加入。请添加主编微信meta-genomics带你入群，务必备注“姓名-单位-研究方向-职称/年级”。高级职称请注明身份，另有海内外微生物PI群供大佬合作交流。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍未解决群内讨论，问题不私聊，帮助同行。

点击阅读原文，跳转最新文章目录阅读