深度学习之CNN卷积神经网络

详解卷积神经网络(CNN)

卷积神经网络（Convolutional Neural Network, CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。

概揽

卷积神经网络（Convolutional Neural Networks / CNNs / ConvNets）与普通神经网络非常相似，它们都由具有可学习的权重和偏置常量(biases)的神经元组成。每个神经元都接收一些输入，并做一些点积计算，输出是每个分类的分数，普通神经网络里的一些计算技巧到这里依旧适用。

所以哪里不同呢？卷积神经网络默认输入是图像，可以让我们把特定的性质编码入网络结构，使是我们的前馈函数更加有效率，并减少了大量参数。

具有三维体积的神经元(3D volumes of neurons)
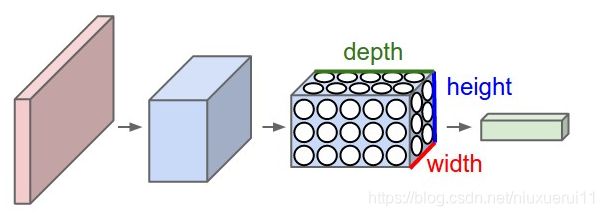
卷积神经网络利用输入是图片的特点，把神经元设计成三个维度 ： width, height, depth(注意这个depth不是神经网络的深度，而是用来描述神经元的) 。比如输入的图片大小是 32 × 32 × 3 (rgb)，那么输入神经元就也具有 32×32×3 的维度。下面是图解：

卷积神经网络

卷积神经网络（平面）组成：输入层、整流层，池化层，输出层

全连接神经网络

全连接神经网络（平面），组成：输入层、激活函数、全连接层

卷积神经网络
一个卷积神经网络有多层构成，他们的输入是三维的，输出也是三维的，有的层有参数，有的层不需要参数，

在卷积神经网络中有一个重要的概念：深度

卷积层
卷积：在原始的输入上进行特征的提取。特征提取简言之就是，在原始输入上一个小区域一个小区域进行特征的提取，稍后细致讲解卷积的计算过程。

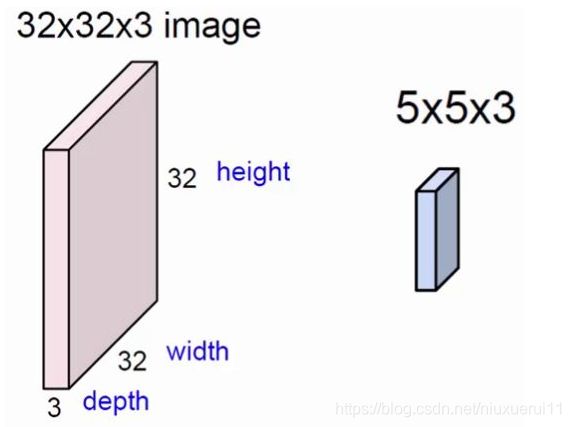
上图中，左方块是输入层，尺寸为3232的3通道图像。右边的小方块是filter，尺寸为55，深度为3。将输入层划分为多个区域，用filter这个固定尺寸的助手，在输入层做运算，最终得到一个深度为1的特征图。

上图中，展示出一般使用多个filter分别进行卷积，最终得到多个特征图。

上图使用了6个filter分别卷积进行特征提取，最终得到6个特征图。将这6层叠在一起就得到了卷积层输出的结果。

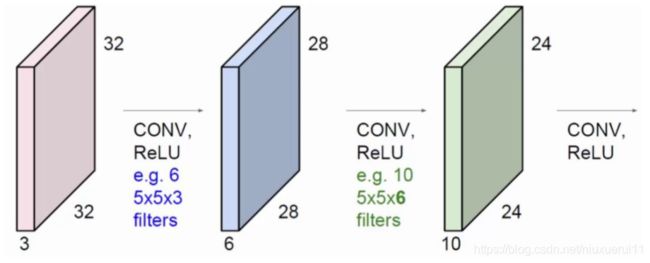
卷积不仅限于对原始输入的卷积。蓝色方块是在原始输入上进行卷积操作，使用了6个filter得到了6个提取特征图。绿色方块还能对蓝色方块进行卷积操作，使用了10个filter得到了10个特征图。每一个filter的深度必须与上一层输入的深度相等。

直观理解卷积

以上图为例：

第一次卷积可以提取出低层次的特征。

第二次卷积可以提取出中层次的特征。

第三次卷积可以提取出高层次的特征。

特征是不断进行提取和压缩的，最终能得到比较高层次特征，简言之就是对原式特征一步又一步的浓缩，最终得到的特征更可靠。利用最后一层特征可以做各种任务：比如分类、回归等。

卷积计算流程

左区域的三个大矩阵是原式图像的输入，RGB三个通道用三个矩阵表示，大小为773。

Filter W0表示1个filter助手，尺寸为3*3，深度为3（三个矩阵）；Filter W1也表示1个filter助手。因为卷积中我们用了2个filter，因此该卷积层结果的输出深度为2（绿色矩阵有2个）。

Bias b0是Filter W0的偏置项，Bias b1是Filter W1的偏置项。

OutPut是卷积后的输出，尺寸为3*3，深度为2。

计算过程：

输入是固定的，filter是指定的，因此计算就是如何得到绿色矩阵。第一步，在输入矩阵上有一个和filter相同尺寸的滑窗，然后输入矩阵的在滑窗里的部分与filter矩阵对应位置相乘：

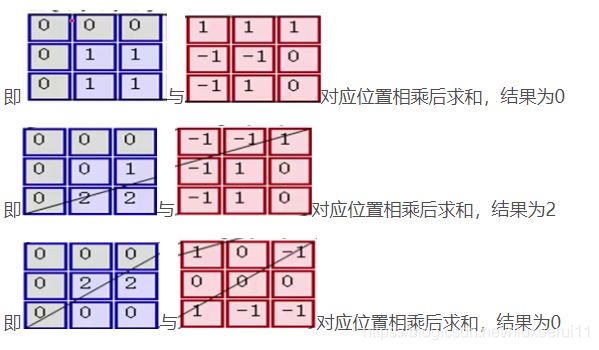
第二步，将3个矩阵产生的结果求和，并加上偏置项，即0+2+0+1=3，因此就得到了输出矩阵的左上角的3：

第三步，让每一个filter都执行这样的操作，变可得到第一个元素：

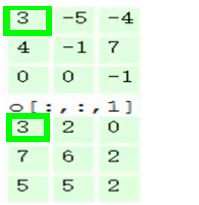
第四步，滑动窗口2个步长，重复之前步骤进行计算

第五步，最终可以得到，在2个filter下，卷积后生成的深度为2的输出结果：

Layers used to build ConvNets

卷积神经网络通常包含以下几种层：

卷积层（Convolutional layer），卷积神经网路中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。
线性整流层（Rectified Linear Units layer, ReLU layer），这一层神经的活性化函数（Activation function）使用线性整流（Rectified Linear Units, ReLU）。
池化层（Pooling layer），通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取其最大值或平均值，得到新的、维度较小的特征。
全连接层（ Fully-Connected layer）, 把所有局部特征结合变成全局特征，用来计算最后每一类的得分。

一个卷积神经网络各层应用实例

卷积——激活——卷积——激活——池化——…——池化——全连接——分类或回归

卷积层（Convolutional layer）

局部感知（Local Connectivity）

普通神经网络把输入层和隐含层进行“全连接(Full Connected)“的设计。从计算的角度来讲，相对较小的图像从整幅图像中计算特征是可行的。但是，如果是更大的图像（如 96x96 的图像），要通过这种全联通网络的这种方法来学习整幅图像上的特征，从计算角度而言，将变得非常耗时。你需要设计 10 的 4 次方（=10000）个输入单元，假设你要学习 100 个特征，那么就有 10 的 6 次方个参数需要去学习。与 28x28 的小块图像相比较， 96x96 的图像使用前向输送或者后向传导的计算方式，计算过程也会慢 10 的 2 次方（=100）倍。

卷积层解决这类问题的一种简单方法是对隐含单元和输入单元间的连接加以限制：每个隐含单元仅仅只能连接输入单元的一部分。例如，每个隐含单元仅仅连接输入图像的一小片相邻区域。（对于不同于图像输入的输入形式，也会有一些特别的连接到单隐含层的输入信号“连接区域”选择方式。如音频作为一种信号输入方式，一个隐含单元所需要连接的输入单元的子集，可能仅仅是一段音频输入所对应的某个时间段上的信号。)

每个隐含单元连接的输入区域大小叫r神经元的感受野(receptive field)。

由于卷积层的神经元也是三维的，所以也具有深度。卷积层的参数包含一系列过滤器（filter），每个过滤器训练一个深度，有几个过滤器输出单元就具有多少深度。

具体如下图所示，样例输入单元大小是32×32×3, 输出单元的深度是5, 对于输出单元不同深度的同一位置，与输入图片连接的区域是相同的，但是参数（过滤器）不同。

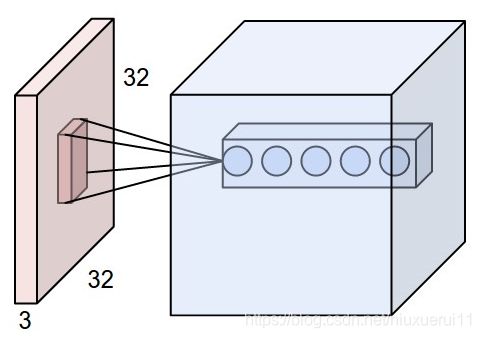
虽然每个输出单元只是连接输入的一部分，但是值的计算方法是没有变的，都是权重和输入的点积，然后加上偏置，这点与普通神经网络是一样的，如下图所示：

空间排列（Spatial arrangement）

一个输出单元的大小有以下三个量控制：depth, stride 和 zero-padding。

深度(depth) : 顾名思义，它控制输出单元的深度，也就是filter的个数，连接同一块区域的神经元个数。又名：depth column
步幅(stride)：它控制在同一深度的相邻两个隐含单元，与他们相连接的输入区域的距离。如果步幅很小（比如 stride = 1）的话，相邻隐含单元的输入区域的重叠部分会很多; 步幅很大则重叠区域变少。
补零(zero-padding) ： 我们可以通过在输入单元周围补零来改变输入单元整体大小，从而控制输出单元的空间大小。

我们先定义几个符号：

输入单元的大小（宽或高）

感受野(receptive field)

步幅（stride）

补零（zero-padding)的数量

深度，输出单元的深度
则可以用以下公式计算一个维度（宽或高）内一个输出单元里可以有几个隐藏单元：

如果计算结果不是一个整数，则说明现有参数不能正好适合输入，步幅（stride）设置的不合适，或者需要补零，证明略，

参数共享(Parameter Sharing)

应用参数共享可以大量减少参数数量，参数共享基于一个假设：如果图像中的一点（x1, y1）包含的特征很重要，那么它应该和图像中的另一点（x2, y2）一样重要。换种说法，我们把同一深度的平面叫做深度切片(depth slice)（(e.g. a volume of size [55x55x96] has 96 depth slices, each of size [55x55])），那么同一个切片应该共享同一组权重和偏置。我们仍然可以使用梯度下降的方法来学习这些权值，只需要对原始算法做一些小的改动， 这里共享权值的梯度是所有共享参数的梯度的总和。

我们不禁会问为什么要权重共享呢？一方面，重复单元能够对特征进行识别，而不考虑它在可视域中的位置。另一方面，权值共享使得我们能更有效的进行特征抽取，因为它极大的减少了需要学习的自由变量的个数。通过控制模型的规模，卷积网络对视觉问题可以具有很好的泛化能力。

卷积（Convolution）

如果应用参数共享的话，实际上每一层计算的操作就是输入层和权重的卷积！这也就是卷积神经网络名字的由来。

先抛开卷积这个概念不管。为简便起见，考虑一个大小为5×5的图像，和一个3×3的卷积核。这里的卷积核共有9个参数，就记为 吧。这种情况下，卷积核实际上有9个神经元，他们的输出又组成一个3×3的矩阵，称为特征图。第一个神经元连接到图像的第一个3×3的局部，第二个神经元则连接到第二个局部（注意，有重叠！就跟你的目光扫视时也是连续扫视一样）。具体如下图所示。

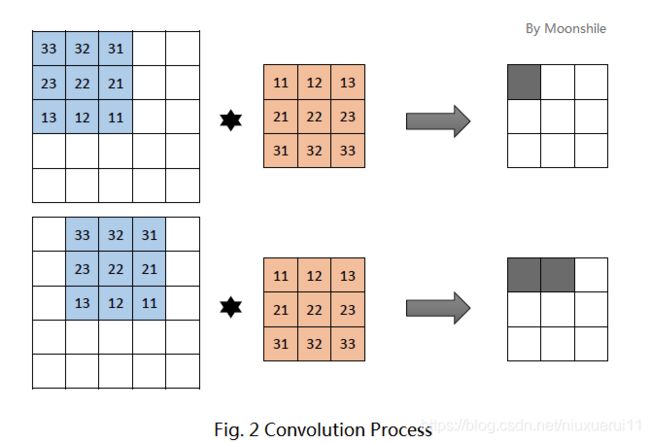
图的上方是第一个神经元的输出，下方是第二个神经元的输出。每个神经元的运算依旧是

需要注意的是，平时我们在运算时，习惯使用 这种写法，但事实上，我们这里使用的是 。

现在我们回忆一下离散卷积运算。假设有二维离散函数 , ， 那么它们的卷积定义为
现在发现了吧！上面例子中的9个神经元均完成输出后，实际上等价于图像和卷积核的卷积操作！

池化层(Pooling Layer)

池化（pool）即下采样（downsamples），目的是为了减少特征图。池化操作对每个深度切片独立，规模一般为 2＊2，相对于卷积层进行卷积运算，池化层进行的运算一般有以下几种：

• 最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。
• 均值池化（Mean Pooling）。取4个点的均值。
• 高斯池化。借鉴高斯模糊的方法。不常用。
• 可训练池化。训练函数 ff ，接受4个点为输入，出入1个点。不常用。

最常见的池化层是规模为2*2， 步幅为2，对输入的每个深度切片进行下采样。每个MAX操作对四个数进行，如下图所示：

池化操作将保存深度大小不变。

如果池化层的输入单元大小不是二的整数倍，一般采取边缘补零（zero-padding）的方式补成2的倍数，然后再池化。

全连接层（Fully-connected layer）

全连接层和卷积层可以相互转换：

• 对于任意一个卷积层，要把它变成全连接层只需要把权重变成一个巨大的矩阵，其中大部分都是0 除了一些特定区块（因为局部感知），而且好多区块的权值还相同（由于权重共享）。
• 相反地，对于任何一个全连接层也可以变为卷积层。比如，一个 的全连接层，输入层大小为 ，它可以等效为一个 的卷积层。换言之，我们把 filter size 正好设置为整个输入层大小。

卷积神经网络架构

Layer Patterns

常见的卷积神经网络架构是这样的：

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

堆叠几个卷积和整流层，再加一个池化层，重复这个模式知道图片已经被合并得比较小了，然后再用全连接层控制输出。

上述表达式中 ? 意味着0次或1次，通常情况下：N >= 0 && N <= 3, M >= 0, K >= 0 && K < 3。

比如你可以组合出以下几种模式：

• INPUT -> FC, 实现了一个线性分类器， 这里 N = M = K = 0
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC. Here we see that there is a single CONV layer between every POOL layer.
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC Here we see two CONV layers stacked before every POOL layer. This is generally a good idea for larger and deeper networks, because multiple stacked CONV layers can develop more complex features of the input volume before the destructive pooling operation.

Layer Sizing Patterns

Input layer : 应该是2的整数次幂。比如32，64， 128等。
Conv Layer : 使用小的过滤器（filter），, 步幅 ，如果不能恰好拟合输入层，还要边缘补零。如果使用 ，那么输出大小将与输入一样。如果用更大的过滤器（比如7*7），一般只会在紧挨着原始输入图片的卷积层才会看到。
Pool Layer :