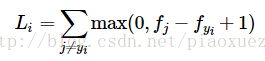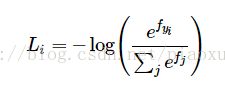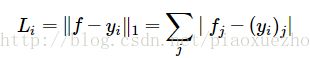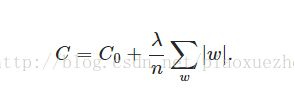斯坦福大学深度学习公开课cs231n学习笔记(7)神经网络防止数据过拟合:损失函数和正则化
在第二节课中,大概提到了线性分类器的损失函数和正则化方法,类似的,在神经网络中也会用到这几个概念方法。这里我没有按照课中先正则化后损失函数的顺序做笔记,还是先说损失函数(也叫代价函数)部分。
损失函数
损失函数是一个有监督学习问题,用于衡量分类算法的预测结果(分类评分)和真实结果之间的一致性。数据损失是所有样本数据损失的平均值:
![]() ,神经网络在实际应用时常用来解决的问题是:分类问题和回归问题。
,神经网络在实际应用时常用来解决的问题是:分类问题和回归问题。
分类问题中,常用的损失函数有 SVM,Softmax。
SVM对应的损失函数表达式:
Softmax对应的损失函数为:
当标签集非常大(例如字典中的所有英语单词,或ImageNet中的22000种分类),需要使用分层Softmax(Hierarchical Softmax)分类:分层softmax是将标签分解为一个树,每个标签对应这个树上的一个路径,树的每个节点都通过训练一个Softmax分类器来做决策,已确定树的左分支还是右分支。
回归问题:即预测问题,例如预测房价等。对于回归问题,通常是计算预测值和真实值之间的损失,使用L2范式或L1范式去度量损失差异。
课中给出的建议:在面对一个回归问题时,首先考虑将输出变成二值化是否确实不够用,如果确信分类不适用,在考虑使用L2损失。例如对一个产品的星级进行预测时,使用5个独立的分类器打分成1-5星的做法,一般会比使用回归损失取得的效果要好。另外分类可以给出关于回归的输出分布,而不是仅仅给出一个简单的输出值。
原因是:(1)L2损失与Softmax损失相比,不如Softmax稳定,同时最优化过程也更困难;(2)L2损失更要求每个输入都要输出一个确切的正确值;而Softmax对于每个评分的准确值要求并不严格;(3)L2损失鲁棒性能比Softmax要差,因为异常值可以导致很大的梯度。(4)L2非常脆弱,在神经网络中使用随机失活(尤其是在L2损失层的上一层)。
正则化
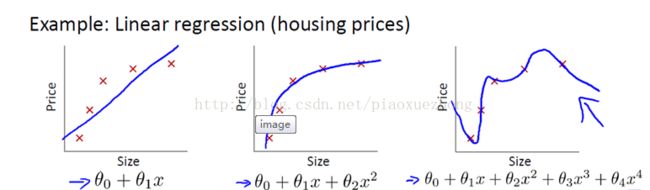
正则化主要是为了防止数据的过拟合,对于过拟合,下图1的说明比较清楚:
对于房价与房子大小之间的关系,左边给出的是线性关系,相比于中间的二次曲线,关系拟合性上稍显不足,为欠拟合;右边的四次曲线很好的过了每格样本点,但是应用到其他的数据上的能力(泛化能力)有些差,右图所示即为过拟合。
对于防止神经网络出现过拟合现象,课中给出了四种方法,分别为:L2正则化,L1正则化,最大范数约束和随机失活方法。
L2正则化:
在代价函数后面加上一个L2正则化项:
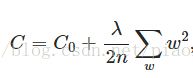
其中,C0代表原始的代价函数,后面那一项就是L2正则化项,λ就是正则项系数,也代表正则化强度,用来权衡正则项与C0项的比重。系数1/2主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好为1。
L2正则化可以理解为对于大数值的权重向量进行严厉惩罚,使得权重向量更加分散。由于输入和权重的乘法操作,一个优良的特性是:使网络倾向于使用所有的输入特征,而不是严重依赖于输入特征的一小部分特征。在梯度下降和参数更新时,L2正则化使得所有权重都以w -= lambda * w 线性下降,往0靠拢。
L1正则化:
在代价函数后面加上一个L1正则化项,即所有权重的绝对值的和,乘以λ/n
L1正则化中的参数和L2正则化类似,另外L1正则化会让权重向量在最优化的过程中变得稀疏(即非常接近于0)。使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集,同时噪音输入几乎不变。
和L1正则化相比,L2正则化中的权重向量大多是分散的小数字。在实践中,L2正则化一般会比L1正则化效果要好。
最大范数约束:
给每个神经元的权重向量设定上限,并使用投影梯度下降确保这一约束。在实践中,与之对应的是参数更新方式不变,然后要求神经元中的权重向量![]() 必须满足=
必须满足=![]() ,一般C值为3或者4。这可以使得当学习率设置过高的时候,不会出现数值“爆炸”。
,一般C值为3或者4。这可以使得当学习率设置过高的时候,不会出现数值“爆炸”。
随机失活(dropout):
左边神经网络在训练时,随机地“删除”一些隐层单元,得到右边的网络。在测试过程中如果不使用随机失活,可看成是对数量巨大的子网络们做模型集成,以此计算出平均预测。课中给出的随机失活代码实现:
""" Vanilla Dropout: Not recommended implementation (see notes below) """
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p # second dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3predict函数不进行随机失活,但对两个隐层的输出都乘以p,来调整数值范围。在测试时所有神经元都能看见它们的输入,需要神经元的输出与训练时的预期输出保持一致。例如,p=0.5,表示在测试时神经元将其输出减半,因为在训练时,它们的输出只有一半(另一半被随机失活了)。在测试时神经元总是激活的,需要调整 x->px 来保持同样的预期输出。
随机失活必须在测试时对激活数据按照 p 进行数值范围调整,测试性能是很关键的,所以在实际应用时更倾向使用反向随机失活(inverted dropout),即是在训练时进行数值范围调整,使前向传播在测试时保持不变。这样还可以保证,无论是否使用随机失活,预测方法的代码保持不变。课中给出的反向随机失活的代码如下:
"""
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3注意区别随机失活,一个是在测试阶段,一个是在训练阶段。
在实际应用中,常使用交叉验证获得一个全局使用的L2正则化强度;或是使用L2正则化的同时在所有层后面使用随机失活,p值一般默认设为0.5。
参考:
http://cs231n.github.io/neural-networks-2/
https://zhuanlan.zhihu.com/p/21560667?refer=intelligentunit
http://blog.csdn.net/u012162613/article/details/44261657
https://www.cnblogs.com/jianxinzhou/p/4083921.html