关于ShardingSphere内置分片算法及其数据倾斜问题总结
ShardingSphere是一款不错的分库分表中间件，并且其内置提供了多种分片算法。但是使用内置的分片算法会造成数据倾斜问题。下面以5.2.0版本的ShardingSphere详细介绍下几种内置分片算法并且分析下数据倾斜问题。
一、ShardingSphere内置分片算法介绍
根据官网描述，ShardingSphere内置提供了多种分片算法，能够满足用户绝大多数业务场景的需要。
按照类型可以划分为自动分片算法、标准分片算法、复合分片算法和 Hint 分片算法。其中，自动分片算法包括：取模分片算法，哈希取模分片算法，基于分片容量的范围分片算法，基于分片边界的范围分片算法，自动时间段分片算法。标准分片算法包括：行表达式分片算法，时间范围分片算法。复合分片算法只有复合行表达式分片算法。Hint 分片算法只有Hint 行表达式分片算法。
下面详细介绍下ShardingSphere内置的几种分片算法。
1、自动分片算法
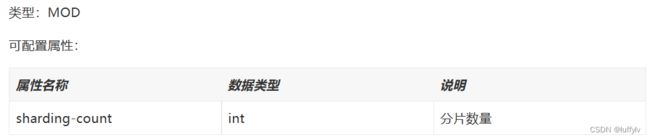
1.1取模分片算法
其中，分片数量是分库数量或分表数量。
该算法的实现类是org.apache.shardingsphere.sharding.algorithm.sharding.mod.ModShardingAlgorithm.java。
该算法的实质是根据分片键的值分别对数据库或表得分片数量取模来分片，所以分片键必须是数字或纯数字的字符串。
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
2.会造成数据倾斜
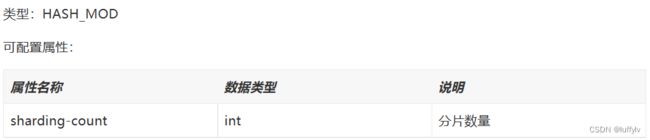
1.2哈希取模分片算法
其中，分片数量是数据库数量或表的数量。
该算法的实现类是org.apache.shardingsphere.sharding.algorithm.sharding.mod.HashModShardingAlgorithm.java。
该算法的本质也是取模，不过是先计算分片键的哈希值，即计算分片值的hashCode的绝对值，然后再根据分片数量来取模。所以该算法允许分片键的值包括数字或字母。
优点：
1. 简单方便
2.算法容易理解
3.分片键的值的类型不受限，支持分片值非纯数字类型
缺点:
1.不方便的快速算出数据落到哪个库哪个表
2.会造成数据倾斜
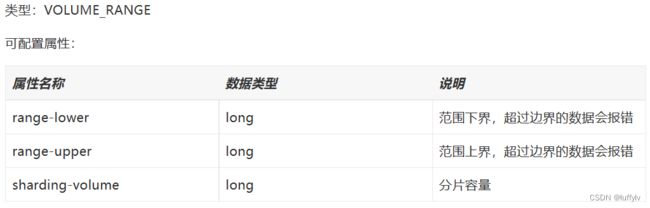
1.3基于分片容量的范围分片算法
其中范围上下界必填，该范围根据分片容量将实数区间分为几个部分，根据分片值在具体哪个区间来确定数据落在具体哪个库表。该算法也要求分片值必须为纯数字类型。
该算法的实现类是org.apache.shardingsphere.sharding.algorithm.sharding.range.VolumeBasedRangeShardingAlgorithm.java。
我们来看下该算法具体是如何进行分片的。我们以四库（db_0、db_1、db_2、db_3）四表（order_0、order_1、order_2、order_3)，分片键为order_id，range-lower=10，range-upper=25，sharding-volume=10为例。该算法根据范围下界，范围上届及分片容量将整个(-∞,+∞)区间分成5部分，分别为(-∞,10)、[10,20)、[20，25)、(25,+∞)。其内部通过calculatePartitionRange方法缓存维护一个分区及其范围的Map
需要注意的是分区数最好和库数或表数相同。比如将上例改为只有两个分库（db_0、db_1)，根据该算法算出该条记录应该在db_2.order_2中，但是没有db_2，此时就会报数据库路由错误。
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
1.4基于分片边界的范围分片算法
该算法与基于分片容量的范围分片算法有些类似，该算法根据设置的分片的范围边界将实数区间分为几个部分，根据分片值在具体哪个区间来确定数据落在具体哪个库表。该算法也要求分片值必须为纯数字类型。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.range.BoundaryBasedRangeShardingAlgorithm.java。
我们来看下该算法具体是如何进行分片的。我们以两库（db_0、db_1）四表（order_0、order_1、order_2、order_3)，分片键为order_id，分库算法的sharding-ranges=8，分表算法的sharding-ranges=1,5,10为例。该算法根据分库的分片的范围边界将整个(-∞,+∞)区间分成两部分，其中0分区对应(-∞,8)，1分区对应[8,+∞)。根据分表的分片的范围边界将整个(-∞,+∞)区间分成四部分，其中0分区对应(-∞,1)，1分区对应[1,5)，2分区对应[5,10)，3分区对应[10,+∞)。若此时order_id=22，则在库的一分区，表的三分区范围内，所以该条记录在db_1.order_3。
需要注意的是分区数最好和库数或表数相同。比如将上例改为只有三个分表（order_0、order_1、order_2)，根据该算法算出该条记录应该在db_1.order_3中，但是没有order_3，此时就会报路由错误。
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
1.5自动时间段分片算法
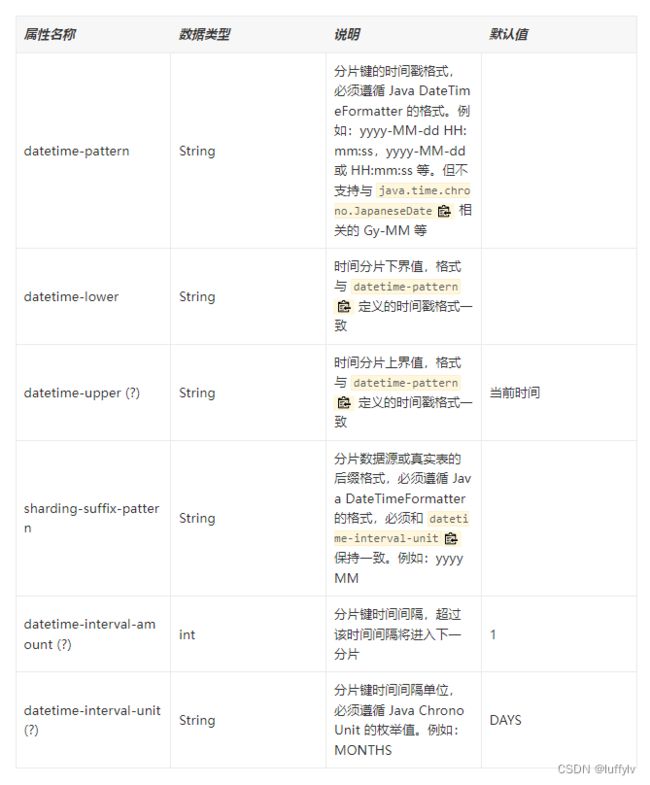
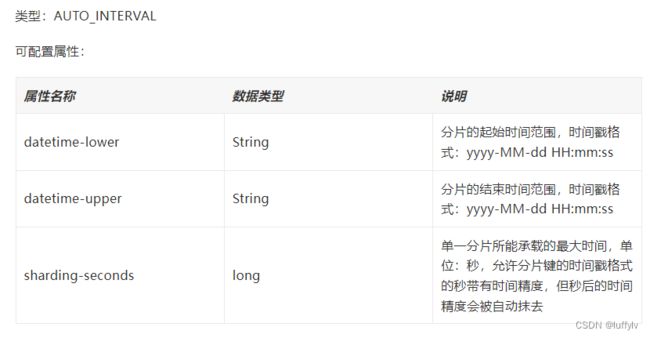该算法针对时间字段类型作为分片键，与前面算法有些类似，都是划分区间，不过不同的是，该算法是将时间进行划分分片。该算法根据设置的分片的起始时间范围、分片的结束时间范围、单一分片所能承载的最大时间，将整个时间区间分为几个部分，根据分片值在具体哪个时间区间来确定数据落在具体哪个库表。
其中，datetime-lower和datetime-upper可以相等，sharding-seconds不能为0。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.datetime.AutoIntervalShardingAlgorithm.java。
我们来看下该算法具体是如何进行分片的。我们以两库（db_0、db_1）四表（order_0、order_1、order_2、order_3)，分片键为order_time，分库算法的datetime-lower=2022-12-21 00 :00:00，datetime-upper=2022-12-21 00 :00:00，sharding-seconds=1。分表算法的datetime-lower=2022-12-21 00:00:00，datetime-upper=2022-12-21 00:00:10，sharding-seconds=5为例。该算法根据分库的配置参数将整个时间区间分成两部分，其中0分区对应(-∞,2022-12-21 00 :00:00]，1分区对应(2022-12-21 00 :00:00,+∞)。根据分表的配置参数将整个时间区间分成四部分，其中0分区对应(-∞,2022-12-21 00 :00:00]，1分区对应(2022-12-21 00 :00:00,2022-12-21 00 :00:05]，2分区对应(2022-12-21 00 :00:05,2022-12-21 00 :00:10]，3分区对应(2022-12-21 00 :00:10,+∞)。若此时order_time=2022-12-21 00 :00:06，则在库的一分区，表的二分区范围内，所以该条记录在db_1.order_2。
需要注意的是分区数最好和库数或表数相同。比如将上例改为只有两个分表（order_0、order_1)，根据该算法算出该条记录应该在db_1.order_2中，但是没有order_2，此时就会报路由错误。
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键类型受限，必须时间字段类型
2.会造成数据倾斜
2、标准分片算法
2.1行表达式分片算法
使用 Groovy 的表达式，提供对 SQL 语句中的 = 和 IN 的分片操作支持，只支持单分片键。 对于简单的分片算法，可以通过简单的配置使用，从而避免繁琐的 Java 代码开发，如: t_user_$->{u_id % 8} 表示 t_user 表根据 u_id 模 8，而分成 8 张表，表名称为 t_user_0 到 t_user_7。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.inline.InlineShardingAlgorithm.java。
其核心也是根据分片键的值对分片数量进行取模。
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
2.会造成数据倾斜
2.2时间范围分片算法
此算法主动忽视了 datetime-pattern 的时区信息。 这意味着当 datetime-lower, datetime-upper 和传入的分片键含有时区信息时，不会因为时区不一致而发生时区转换。 当传入的分片键为 java.time.Instant 时存在特例处理，其会携带上系统的时区信息后转化为 datetime-pattern 的字符串格式，再进行下一步分片。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.datetime.IntervalShardingAlgorithm.java
我们来看下该算法具体是如何进行分片的。以四表（order_20221201、order_20221202、order_20221203、order_20221204)，分片键为order_time，分表算法的datetime-pattern=yyyy-MM-dd HH:mm:ss，datetime-lower=2022-12-01 00 :00:00，datetime-upper=2022-12-04 00 :00:00，sharding-suffix-pattern=yyyyMMdd，datetime-interval-amount=1为例。若此时order_time=2022-12-03 15:00:00，根据算法计算，后缀为20221203，则该数据落在order_20221203表中。
需要注意的是分区数最好和库数或表数相同。比如将上例改为只有两个分表（order_20221201、order_20221202)，根据该算法算出该条记录应该在order_20221203中，但是没有order_20221203表，此时就会报路由错误。
优点：
1. 简单方便
2.算法容易理解
3.适合将某一时间段的数据存储一张表的情况，比如每天数据存储一张表， 或每月或每个季度或每年等数据存储一张表。
缺点:
1.算法配置较麻烦
2.分片键类型受限，必须时间字段类型
3.会造成数据倾斜
3、复合分片算法
3.1复合行表达式分片算法
该算法支持分片键多字段的情况，其中sharding-columns如果只配置一个字段，那么该算法将退化为行表达式分片算法。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.complex.ComplexInlineShardingAlgorithm.java
我们来看下该算法具体是如何进行分片的。以四表（order_00, order_01, order_10, order_11)，分片键为type和order_id，分表算法的sharding-columns=type,order_id，algorithm-expression=order_${type % 2}${order_id % 2}为例。若此时type=1, order_id=4，根据算法计算，type % 2=1，order_id % 2 = 0，则该数据落在order_10表中。
优点：
1. 简单方便
2.算法容易理解
3.支持多个分片键
4.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
2.会造成数据倾斜
4、Hint 分片算法
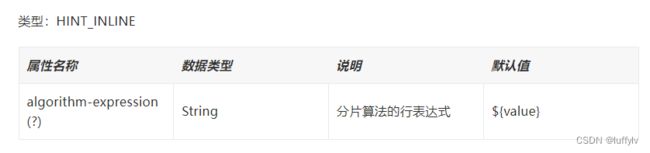
4.1Hint 行表达式分片算法
该算法和行表达式分片算法很类似，不同的是可以不配置algorithm-expression属性，不配置的话默认是找表名为分片键的值的表。
该算法的实现类是 org.apache.shardingsphere.sharding.algorithm.sharding.hint.HintInlineShardingAlgorithm.java
优点：
1. 简单方便
2.算法容易理解
3.可以方便的算出数据落到哪个库哪个表
缺点:
1.分片键的值的类型受限，必须是纯数字，不能包括字母等
2.会造成数据倾斜
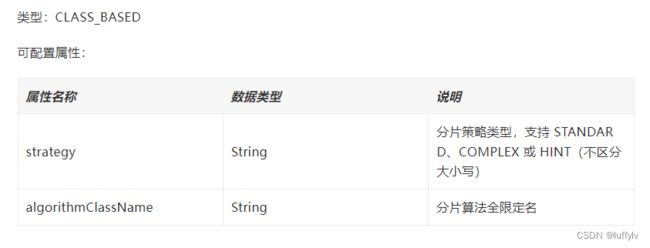
5、自定义类分片算法
通过配置分片策略类型和算法类名，实现自定义扩展。 CLASS_BASED 允许向算法类内传入额外的自定义属性，传入的属性可以通过属性名为 props 的 java.util.Properties 类实例取出。
如果strategy=STANDAR，则自定义算法类需要实现org.apache.shardingsphere.sharding.api.sharding.standard.StandardShardingAlgorithm.java接口；strategy=COMPLEX，则自定义算法类需要实现org.apache.shardingsphere.sharding.api.sharding.complex.ComplexKeysShardingAlgorithm.java接口；strategy=HINT，则自定义算法类需要实现org.apache.shardingsphere.sharding.api.sharding.hint.HintShardingAlgorithm.java接口。
优点：
1. 可以根据业务情况实现自己的分库分表算法，算法较灵活
2.分片键的值可以是任意形式
3.一定程度上可以避免数据倾斜问题
缺点:
1.需要通过Java类的形式实现分库分表策略，增加编码量
二、ShardingSphere内置分片算法的数据倾斜问题
此处所谓的数据倾斜是指，在通过分片算法后大量数据落在某些库表中，导致另某些库表中只有少量或没有数据，导致数据分布不够均匀。
通过上面关于ShardingSphere内置分片算法的介绍，我们可以根据实际的业务情况选择适合的分片算法。如果希望按时间段分片可以选择自动时间段分片算法或者时间范围分片算法。但是该算法也存在因为某些时间段数据激增，某些时间段数据量很少导致数据倾斜。而以按数据库数或表数取模的算法则会存在永远不会有数据落在某些表中的情况。取模分片算法、哈希取模分片算法的实质就是取模。行表达式分片算法、复合行表达式分片算法、Hint 行表达式分片算法的取模形式的行表达式算法也会存在这个问题。比方说，我们按5库20表进行发分库分表，只有分片键是0或是5的倍数才会落到0库，但是又因为是20表，所以落到0库的数据只会分布在0或5或10或15这4个表中，导致路由到0库的数据永远不会落到除上述4个表的其他16个表中，这严重违背了我们的初衷。
下面是分别以2库3表和5库20表，分片值从0-200对库表数进行取模分片的分库分表演算。
| 分片值 | 2库3表 | 5库20表 | ||
| 2库 | 3表 | 5库 | 20表 | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 2 | 2 | 2 |
| 3 | 1 | 0 | 3 | 3 |
| 4 | 0 | 1 | 4 | 4 |
| 5 | 1 | 2 | 0 | 5 |
| 6 | 0 | 0 | 1 | 6 |
| 7 | 1 | 1 | 2 | 7 |
| 8 | 0 | 2 | 3 | 8 |
| 9 | 1 | 0 | 4 | 9 |
| 10 | 0 | 1 | 0 | 10 |
| 11 | 1 | 2 | 1 | 11 |
| 12 | 0 | 0 | 2 | 12 |
| 13 | 1 | 1 | 3 | 13 |
| 14 | 0 | 2 | 4 | 14 |
| 15 | 1 | 0 | 0 | 15 |
| 16 | 0 | 1 | 1 | 16 |
| 17 | 1 | 2 | 2 | 17 |
| 18 | 0 | 0 | 3 | 18 |
| 19 | 1 | 1 | 4 | 19 |
| 20 | 0 | 2 | 0 | 0 |
| 21 | 1 | 0 | 1 | 1 |
| 22 | 0 | 1 | 2 | 2 |
| 23 | 1 | 2 | 3 | 3 |
| 24 | 0 | 0 | 4 | 4 |
| 25 | 1 | 1 | 0 | 5 |
| 26 | 0 | 2 | 1 | 6 |
| 27 | 1 | 0 | 2 | 7 |
| 28 | 0 | 1 | 3 | 8 |
| 29 | 1 | 2 | 4 | 9 |
| 30 | 0 | 0 | 0 | 10 |
| 31 | 1 | 1 | 1 | 11 |
| 32 | 0 | 2 | 2 | 12 |
| 33 | 1 | 0 | 3 | 13 |
| 34 | 0 | 1 | 4 | 14 |
| 35 | 1 | 2 | 0 | 15 |
| 36 | 0 | 0 | 1 | 16 |
| 37 | 1 | 1 | 2 | 17 |
| 38 | 0 | 2 | 3 | 18 |
| 39 | 1 | 0 | 4 | 19 |
| 40 | 0 | 1 | 0 | 0 |
| 41 | 1 | 2 | 1 | 1 |
| 42 | 0 | 0 | 2 | 2 |
| 43 | 1 | 1 | 3 | 3 |
| 44 | 0 | 2 | 4 | 4 |
| 45 | 1 | 0 | 0 | 5 |
| 46 | 0 | 1 | 1 | 6 |
| 47 | 1 | 2 | 2 | 7 |
| 48 | 0 | 0 | 3 | 8 |
| 49 | 1 | 1 | 4 | 9 |
| 50 | 0 | 2 | 0 | 10 |
| 51 | 1 | 0 | 1 | 11 |
| 52 | 0 | 1 | 2 | 12 |
| 53 | 1 | 2 | 3 | 13 |
| 54 | 0 | 0 | 4 | 14 |
| 55 | 1 | 1 | 0 | 15 |
| 56 | 0 | 2 | 1 | 16 |
| 57 | 1 | 0 | 2 | 17 |
| 58 | 0 | 1 | 3 | 18 |
| 59 | 1 | 2 | 4 | 19 |
| 60 | 0 | 0 | 0 | 0 |
| 61 | 1 | 1 | 1 | 1 |
| 62 | 0 | 2 | 2 | 2 |
| 63 | 1 | 0 | 3 | 3 |
| 64 | 0 | 1 | 4 | 4 |
| 65 | 1 | 2 | 0 | 5 |
| 66 | 0 | 0 | 1 | 6 |
| 67 | 1 | 1 | 2 | 7 |
| 68 | 0 | 2 | 3 | 8 |
| 69 | 1 | 0 | 4 | 9 |
| 70 | 0 | 1 | 0 | 10 |
| 71 | 1 | 2 | 1 | 11 |
| 72 | 0 | 0 | 2 | 12 |
| 73 | 1 | 1 | 3 | 13 |
| 74 | 0 | 2 | 4 | 14 |
| 75 | 1 | 0 | 0 | 15 |
| 76 | 0 | 1 | 1 | 16 |
| 77 | 1 | 2 | 2 | 17 |
| 78 | 0 | 0 | 3 | 18 |
| 79 | 1 | 1 | 4 | 19 |
| 80 | 0 | 2 | 0 | 0 |
| 81 | 1 | 0 | 1 | 1 |
| 82 | 0 | 1 | 2 | 2 |
| 83 | 1 | 2 | 3 | 3 |
| 84 | 0 | 0 | 4 | 4 |
| 85 | 1 | 1 | 0 | 5 |
| 86 | 0 | 2 | 1 | 6 |
| 87 | 1 | 0 | 2 | 7 |
| 88 | 0 | 1 | 3 | 8 |
| 89 | 1 | 2 | 4 | 9 |
| 90 | 0 | 0 | 0 | 10 |
| 91 | 1 | 1 | 1 | 11 |
| 92 | 0 | 2 | 2 | 12 |
| 93 | 1 | 0 | 3 | 13 |
| 94 | 0 | 1 | 4 | 14 |
| 95 | 1 | 2 | 0 | 15 |
| 96 | 0 | 0 | 1 | 16 |
| 97 | 1 | 1 | 2 | 17 |
| 98 | 0 | 2 | 3 | 18 |
| 99 | 1 | 0 | 4 | 19 |
| 100 | 0 | 1 | 0 | 0 |
| 101 | 1 | 2 | 1 | 1 |
| 102 | 0 | 0 | 2 | 2 |
| 103 | 1 | 1 | 3 | 3 |
| 104 | 0 | 2 | 4 | 4 |
| 105 | 1 | 0 | 0 | 5 |
| 106 | 0 | 1 | 1 | 6 |
| 107 | 1 | 2 | 2 | 7 |
| 108 | 0 | 0 | 3 | 8 |
| 109 | 1 | 1 | 4 | 9 |
| 110 | 0 | 2 | 0 | 10 |
| 111 | 1 | 0 | 1 | 11 |
| 112 | 0 | 1 | 2 | 12 |
| 113 | 1 | 2 | 3 | 13 |
| 114 | 0 | 0 | 4 | 14 |
| 115 | 1 | 1 | 0 | 15 |
| 116 | 0 | 2 | 1 | 16 |
| 117 | 1 | 0 | 2 | 17 |
| 118 | 0 | 1 | 3 | 18 |
| 119 | 1 | 2 | 4 | 19 |
| 120 | 0 | 0 | 0 | 0 |
| 121 | 1 | 1 | 1 | 1 |
| 122 | 0 | 2 | 2 | 2 |
| 123 | 1 | 0 | 3 | 3 |
| 124 | 0 | 1 | 4 | 4 |
| 125 | 1 | 2 | 0 | 5 |
| 126 | 0 | 0 | 1 | 6 |
| 127 | 1 | 1 | 2 | 7 |
| 128 | 0 | 2 | 3 | 8 |
| 129 | 1 | 0 | 4 | 9 |
| 130 | 0 | 1 | 0 | 10 |
| 131 | 1 | 2 | 1 | 11 |
| 132 | 0 | 0 | 2 | 12 |
| 133 | 1 | 1 | 3 | 13 |
| 134 | 0 | 2 | 4 | 14 |
| 135 | 1 | 0 | 0 | 15 |
| 136 | 0 | 1 | 1 | 16 |
| 137 | 1 | 2 | 2 | 17 |
| 138 | 0 | 0 | 3 | 18 |
| 139 | 1 | 1 | 4 | 19 |
| 140 | 0 | 2 | 0 | 0 |
| 141 | 1 | 0 | 1 | 1 |
| 142 | 0 | 1 | 2 | 2 |
| 143 | 1 | 2 | 3 | 3 |
| 144 | 0 | 0 | 4 | 4 |
| 145 | 1 | 1 | 0 | 5 |
| 146 | 0 | 2 | 1 | 6 |
| 147 | 1 | 0 | 2 | 7 |
| 148 | 0 | 1 | 3 | 8 |
| 149 | 1 | 2 | 4 | 9 |
| 150 | 0 | 0 | 0 | 10 |
| 151 | 1 | 1 | 1 | 11 |
| 152 | 0 | 2 | 2 | 12 |
| 153 | 1 | 0 | 3 | 13 |
| 154 | 0 | 1 | 4 | 14 |
| 155 | 1 | 2 | 0 | 15 |
| 156 | 0 | 0 | 1 | 16 |
| 157 | 1 | 1 | 2 | 17 |
| 158 | 0 | 2 | 3 | 18 |
| 159 | 1 | 0 | 4 | 19 |
| 160 | 0 | 1 | 0 | 0 |
| 161 | 1 | 2 | 1 | 1 |
| 162 | 0 | 0 | 2 | 2 |
| 163 | 1 | 1 | 3 | 3 |
| 164 | 0 | 2 | 4 | 4 |
| 165 | 1 | 0 | 0 | 5 |
| 166 | 0 | 1 | 1 | 6 |
| 167 | 1 | 2 | 2 | 7 |
| 168 | 0 | 0 | 3 | 8 |
| 169 | 1 | 1 | 4 | 9 |
| 170 | 0 | 2 | 0 | 10 |
| 171 | 1 | 0 | 1 | 11 |
| 172 | 0 | 1 | 2 | 12 |
| 173 | 1 | 2 | 3 | 13 |
| 174 | 0 | 0 | 4 | 14 |
| 175 | 1 | 1 | 0 | 15 |
| 176 | 0 | 2 | 1 | 16 |
| 177 | 1 | 0 | 2 | 17 |
| 178 | 0 | 1 | 3 | 18 |
| 179 | 1 | 2 | 4 | 19 |
| 180 | 0 | 0 | 0 | 0 |
| 181 | 1 | 1 | 1 | 1 |
| 182 | 0 | 2 | 2 | 2 |
| 183 | 1 | 0 | 3 | 3 |
| 184 | 0 | 1 | 4 | 4 |
| 185 | 1 | 2 | 0 | 5 |
| 186 | 0 | 0 | 1 | 6 |
| 187 | 1 | 1 | 2 | 7 |
| 188 | 0 | 2 | 3 | 8 |
| 189 | 1 | 0 | 4 | 9 |
| 190 | 0 | 1 | 0 | 10 |
| 191 | 1 | 2 | 1 | 11 |
| 192 | 0 | 0 | 2 | 12 |
| 193 | 1 | 1 | 3 | 13 |
| 194 | 0 | 2 | 4 | 14 |
| 195 | 1 | 0 | 0 | 15 |
| 196 | 0 | 1 | 1 | 16 |
| 197 | 1 | 2 | 2 | 17 |
| 198 | 0 | 0 | 3 | 18 |
| 199 | 1 | 1 | 4 | 19 |
| 200 | 0 | 2 | 0 | 0 |
个人是不太推荐单纯的根据分片键取模分片算法的，在实际的项目中一直使用的是自定义类分片算法，实质是根据分片键的最后一位数字对数据库数取模，分片键的倒数二三位数字对表数取模。这种方式可以尽量避免数据倾斜问题，不会存在某些库表永远不会有数据的情况。