车间调度丨柔性车间的动态调度问题：重调度

车间调度系列文章：

• 1、车间调度历史文章
• 2、车间调度丨柔性车间的动态调度问题：重调度

引言

重调度：通俗来说，就是重新给出一个调度策略，使整个系统的资源正常流动。简单的用法，就是在之前的车间调度文章中，已经得出一个调度方案，突然机器故障了，这时候需要对调度方案重新修改。这个过程就是车间重调度，具体该怎么实施呢？今天就仔细和大家讨论一下柔性车间中机器故障情况下的重调度问题，该如何建模求解。

柔性车间调度问题

柔性车间调度问题可描述为：多个工件在多台机器上加工，工件安排加工时严格按照工序的先后顺序，至少有一道工序有多个可加工机器，在某些优化目标下安排生产。
柔性车间调度问题的约束条件如下：

• （1）同一台机器同一时刻只能加工一个工件;
• （2）同一工件的同一道工序在同一时刻被加工的机器数是一;
• （3）任意工序开始加工不能中断;
• （4）各个工件之间不存在的优先级的差别;
• （5）同一工件的工序之间存在先后约束，不同工件的工序之间不存在先后约束;
• （6）所有工件在零时刻都可以被加工。

MK01算例：

10 6 2
6 2 1 5 3 4 3 5 3 3 5 2 1 2 3 4 6 2 3 6 5 2 6 1 1 1 3 1 3 6 6 3 6 4 3
5 1 2 6 1 3 1 1 1 2 2 2 6 4 6 3 6 5 2 6 1 1
5 1 2 6 2 3 4 6 2 3 6 5 2 6 1 1 3 3 4 2 6 6 6 2 1 1 5 5
5 3 6 5 2 6 1 1 1 2 6 1 3 1 3 5 3 3 5 2 1 2 3 4 6 2
6 3 5 3 3 5 2 1 3 6 5 2 6 1 1 1 2 6 2 1 5 3 4 2 2 6 4 6 3 3 4 2 6 6 6
6 2 3 4 6 2 1 1 2 3 3 4 2 6 6 6 1 2 6 3 6 5 2 6 1 1 2 1 3 4 2
5 1 6 1 2 1 3 4 2 3 3 4 2 6 6 6 3 2 6 5 1 1 6 1 3 1
5 2 3 4 6 2 3 3 4 2 6 6 6 3 6 5 2 6 1 1 1 2 6 2 2 6 4 6
6 1 6 1 2 1 1 5 5 3 6 6 3 6 4 3 1 1 2 3 3 4 2 6 6 6 2 2 6 4 6
6 2 3 4 6 2 3 3 4 2 6 6 6 3 5 3 3 5 2 1 1 6 1 2 2 6 4 6 2 1 3 4 2

第一行的10,6是工件数和机器数。

第二行第一个加粗的数字6表示，工件1有6道工序。斜体的2 1 5 3 4，表示工件1的第一道工序有两个可选机器，分别是1和3，加工时间是5和4，后面的3 5 3 3 5 2 1表示工件1的第二道工序有3个可选机器，分别是5,3,2，加工时间是3,5,1，一行就是1个工件的所有工序的可选机器可加工时间，后面的工序以此类推。

下面的每一行以此类推。

数学模型

字符说明：

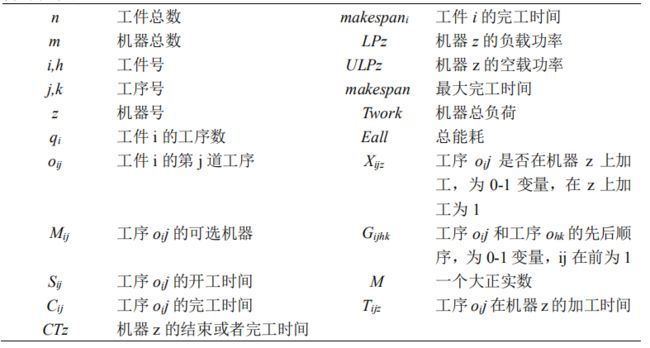
目标函数：

约束条件：

约束条件需要增加一个机器故障约束，大家可自行查阅资料，增加进去。

机器故障

动态问题更符合实际，实际生产中容易出现机器故障、紧急订单等突发状况，解决这些问题至关重要，本文介绍机器故障下的柔性车间调度问题的解决方式，其他问题大同小异。

不管发生什么突发情况，已经完成的生产任务已经是既定事实，所以突发情况前生产计划是已知的、固定的，动态调度是对突发情况后的生产任务进行安排。本文分别在右移重调度方式和完全重调度下对问题进行解决，其中完全重调度采用遗传算法。

本文机器故障对应的参数有：故障机器、故障时间、故障维修时间

机器故障下的假设：同一时刻下其他正在进行生产任务的机器任务不能中断，故障机器下的加工任务重新加工。

MK01的一个可行调度方案方案如下，本文的机器故障下的问题解决这一方案，完工时间是47

w=[9, 1, 7, 9, 9, 3, 1, 4, 3, 1, 5, 7, 9, 0, 6, 4, 0, 4, 6, 3, 7, 2, 8, 5, 8, 1, 2, 9, 2, 6, 5, 8, 4, 0, 0, 8, 2, 7, 6, 2, 3, 6, 9, 3, 4, 8, 0, 5, 5, 7, 8, 5, 0, 1, 4]
m=[[6, 2, 6, 3, 2, 1, 3, 2, 2, 1, 6, 3, 6, 3, 6, 1, 2, 2, 4, 3, 1, 2, 6, 1, 1, 4, 6, 4, 1, 3, 3, 4, 3, 6, 1, 1, 3, 2, 5, 1, 2, 3, 4, 6, 4, 3, 3, 2, 1, 2, 4, 1, 6, 1, 3]]
t=[[2, 6, 2, 4, 1, 1, 1, 1, 6, 2, 2, 4, 1, 4, 1, 1, 1, 6, 2, 1, 1, 6, 1, 2, 1, 6, 2, 6, 1, 4, 4, 3, 4, 2, 1, 2, 4, 6, 1, 1, 1, 1, 2, 2, 6, 4, 1, 6, 1, 6, 6, 3, 6, 1, 4]]

甘特图：

右移重调度下故障问题解决

右移重调度比较简单，简单来说：不改变原始调度方案，故障机器上受到影响的加工任务暂停，机器维修完成后重新开工，相当于工序右移，当然，与受影响任务关联的任务也需要右移。

解码解决：重新解码调度方案的编码：找到其受影响任务在编码的位置，修正其开工时间为故障时间为故障时间加维修时间，代码如下：

def caculate1(self,job,machine,machine_time,error_M,error_S,error_T):
    jobtime=np.zeros((1,self.job_num))        
    tmm=np.zeros((1,self.machine_num))              
    tmmw=np.zeros((1,self.machine_num))         
    startime=0
    list_M,list_S,list_W=[],[],[]
    count=np.zeros((1,self.job_num),dtype=np.int)
    for i in range(job.shape[1]):
        svg=int(job[0,i])
        sig=int(machine[0,i])-1

        startime=max(jobtime[0,svg],tmm[0,sig])
        if(startime<error_S)and(startime+machine_time[0,i]>error_S)and(error_M==sig+1):
            startime=error_S+error_T    
        tmm[0,sig]=startime+machine_time[0,i]
        jobtime[0,svg]=startime+machine_time[0,i]

        list_M.append(sig+1)
        list_S.append(startime)
        list_W.append(machine_time[0,i])
        count[0,svg]+=1

    tmax=np.argmax(tmm[0])+1        #结束最晚的机器
    C_finish=max(tmm[0])            #最晚完工时间
    return C_finish,list_M,list_S,list_W,tmax

error_M,error_S,error_T是故障机器、故障时间、故障维修时间，代码在fjsp.py里

完全重调度下故障问题解决

保持机器故障发生前的调度方案不变，对故障后的生产任务重新安排，本文采用切分的方式，把故障前的加工任务切分成不变的编码，重新生成故障发生的工序、机器、加工时间编码，并用遗传算法对重新生成的编码进行寻优.

本文以介绍求解思路为主，简化遗传算法求解过程：对工序编码进行Pox交叉、对机器编码进行多点变异。

调度方案切分

逻辑：故障发生时所有已经完成和正在加工的工序保持调度方案不变，找到最晚正在加工工序在编码的位置，找到位置后的切分比较容易，不再赘述，找位置的代码如下：

def find_index(self,list_M,list_S,list_W,error_M,error_S,error_T):
    MT=[]
    for i in range(len(list_M)):
        if(list_S[i]<error_S)and(list_S[i]+list_W[i]>error_S):
            MT.append([i,list_M[i]])
    return MT[-1][0]

list_M,list_S,list_W是原调度方案的机器安排，开工时间安排、工序的加工时间，代码在ga.py里。

重调度方案初始化

简单来说：重调度位置后以后的加工工序随机选择加工机器，具体解码方式不再赘述，参考前面推文，代码：

def creat_job(self,job,machine,machine_time,index):
    count=np.zeros((self.job_num,1),dtype=np.int)-1
    job1,job2=job[0,:index+1].tolist(),job[0,index+1:]
    np.random.shuffle(job2)
    work=job1+job2.tolist()
    machine1,machine_time1=machine.copy(),machine_time.copy()
    for i in range(job.shape[1]):
        signal=int(job[0,i])
        count[signal,0]+=1
        if(i>index):
            highs=self.tom[signal][count[signal,0]]
            lows=self.tom[signal][count[signal,0]]-self.tdx[signal][count[signal,0]]
            n_machine=self.Tmachine[signal,lows:highs].tolist()
            n_time=self.Tmachinetime[signal,lows:highs].tolist()
                                #否则随机挑选机器                                
            index1=np.random.randint(0,len(n_time),1)
            machine1[0,i]=n_machine[index1[0]]
            machine_time1[0,i]=n_time[index1[0]]
    return np.array([work]),machine1,machine_time1

job,machine,machine_time是原调度方案的工序、机器、加工时间编码，index是重调度位置，也即调度方案切分的位置，代码在fjsp.py里。

pox交叉

原理不再赘述，对重调度位置后重新生成的工序编码交叉，代码：

job1,job2=job[0,:index+1].tolist(),job[0,index+1:]
def job_cross(self,chrom_L1,chrom_L2):       #工序的pox交叉
    num=list(set(chrom_L1[0]))
    np.random.shuffle(num)
    index=np.random.randint(0,len(num),1)[0]
    jpb_set1=num[:index+1]                  #固定不变的工件
    jpb_set2=num[index+1:]                  #按顺序读取的工件
    C1,C2=np.zeros((1,chrom_L1.shape[1]))-1,np.zeros((1,chrom_L1.shape[1]))-1
    sig,svg=[],[]
    for i in range(chrom_L1.shape[1]):#固定位置的工序不变
        ii,iii=0,0
        for j in range(len(jpb_set1)):
            if(chrom_L1[0,i]==jpb_set1[j]):
                C1[0,i]=chrom_L1[0,i]
            else:
                ii+=1
            if(chrom_L2[0,i]==jpb_set1[j]):
                C2[0,i]=chrom_L2[0,i]
            else:
                iii+=1
        if(ii==len(jpb_set1)):
            sig.append(chrom_L1[0,i])
        if(iii==len(jpb_set1)):
            svg.append(chrom_L2[0,i])
    signal1,signal2=0,0             #为-1的地方按顺序添加工序编码
    for i in range(chrom_L1.shape[1]):
        if(C1[0,i]==-1):
            C1[0,i]=svg[signal1]
            signal1+=1
        if(C2[0,i]==-1):
            C2[0,i]=sig[signal2]
            signal2+=1
    return C1[0].tolist(),C2[0].tolist()

job是重新生成的工序编码，job1是不变的工序编码，job2是pox的工序编码，代码在ga.py里。

多点变异

对重调度位置后多个位置的机器编码进行编码，变异方式是对应工序选择最短加工时间机器。代码：

def ma_mul(self,job,machine,machine_time,index):
    count=np.zeros((self.job_num,1),dtype=np.int)-1
    j=0
    r=np.random.randint(1,job.shape[1]-index)
    idx=np.random.randint(index+1,job.shape[1],r)
    idx=list(set(idx))
    for i in range(job.shape[1]):
        svg=int(job[0,i])
        count[svg,0]+=1
        if(i==idx[j]):
            if(j<len(idx)-1):
                j+=1
            highs=self.tom[svg][count[svg,0]]
            lows=self.tom[svg][count[svg,0]]-self.tdx[svg][count[svg,0]]
            n_machine=self.Tmachine[svg,lows:highs].tolist()
            n_time=self.Tmachinetime[svg,lows:highs].tolist()
            loc_idx=n_time.index(min(n_time))
            machine[0,i]=n_machine[loc_idx]
            machine_time[0,i]=min(n_time)
    return machine,machine_time

代码在ga.py里。

结果

代码运行环境
windows系统，python3.6.0,第三方库及版本号如下：

numpy==1.18.5
matplotlib==3.2.1

第三方库需要在安装完python之后，额外安装，以前文章有讲述过安装第三方库的解决办法。

主函数

设计主函数如下：

job=np.array([w])
machine,machine_time=np.array(m),np.array(t)
job_init=[job,machine,machine_time]
oj=data_deal(10,6)               #工件数，机器数
Tmachine,Tmachinetime,tdx,work,tom,machines=oj.cacu()
print(tom)
print(tdx)
parm_data=[Tmachine,Tmachinetime,tdx,work,tom,machines]
to=FJSP(10,6,0.3,0.4,parm_data)      #工件数，机器数，3种选择的概率和mk01的数据

error_M,error_S,error_T=4,19,4       #故障机器、故障时间、故障维修时间
C_finish,list_M,list_S,list_W,tmax=to.caculate(job,machine,machine_time)
to.draw(job,C_finish,list_M,list_S,list_W,tmax,0,error_M,error_S,error_T) #原始调度方案

C_finish,list_M,list_S,list_W,tmax=to.caculate1(job,machine,machine_time,error_M,error_S,error_T)
to.draw(job,C_finish,list_M,list_S,list_W,tmax,1,error_M,error_S,error_T)#右移重调度方案

ho=GA(20,10,to,0.8,0.2,parm_data,job_init,10)    #20、10、0.8、0.2、10依次是迭代次数，种群规模、交叉概率、变异概率、工件数
#to、parm_data、job_init依次是fjsp模块，mko1数据、初始调度方案
job,machine,machine_time,result=ho.ga_total(error_M,error_S,error_T)
C_finish,list_M,list_S,list_W,tmax=to.caculate1(job,machine,machine_time,error_M,error_S,error_T)
to.draw(job,C_finish,list_M,list_S,list_W,tmax,1,error_M,error_S,error_T)#完全重调度方案

result=np.array(result).reshape(len(result),2)
plt.plot(result[:,0],result[:,1])                   #画完工时间随迭代次数的变化
font1={'weight':'bold','size':22}
plt.xlabel("迭代次数",font1)
plt.title("完工时间变化图",font1)
plt.ylabel("完工时间",font1)
plt.show()

运行结果

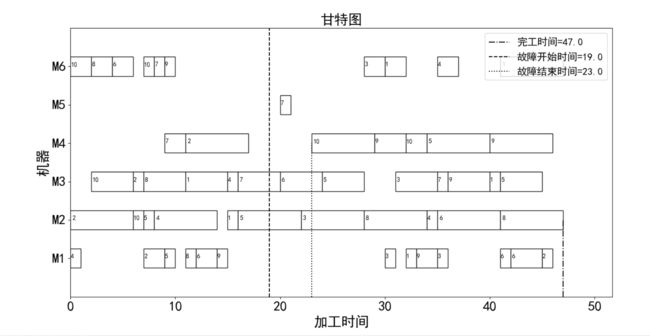
右移重调度结果如下：

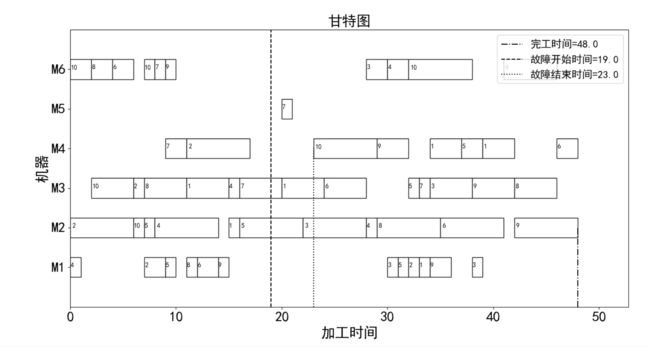
完全重调度结果如下：

完工时间随迭代次数变化如下：

代码

有4个py文件和一个mk01的text文档：

数据集下载：

https://gitee.com/XZDNF-1618/data.git

更多车间调度问题、VRP问题，详见微信公众号：学长带你飞

回复：车间调度，可得文章链接目录。