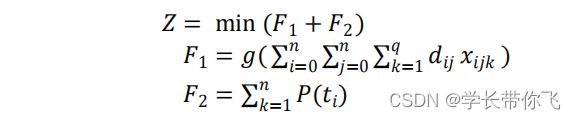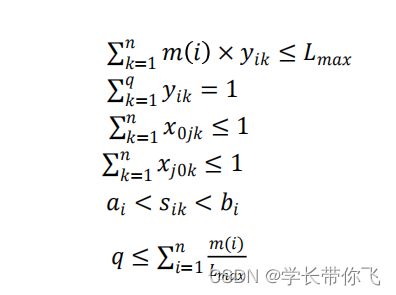路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法：算例RC108

路径优化系列文章：

• 1、路径优化历史文章
• 2、路径优化丨带时间窗和载重约束的CVRPTW问题-改进遗传算法：算例RC108
• 3、路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法：算例RC108

问题描述

带时间窗和载重约束的路径优化问题可描述为：若干配送中心、每个中心有若干配送车辆、存在若干需求点、配送中心往需求点配送货物。其中：车辆存在载重约束，需求点存在时间窗约束。本文假设：

• （1）需求点所需货物量已知，且配送中心能满足所有需求点的货物需求;
• （2）需求点时间窗已知，过早或过晚到达都会受到惩罚;
• （3）需求点位置已知，不考虑货物在需求点的配送时间;
• （4）所有车辆型号和载重相同;
• （5）配送车辆从物资配送中心出发，最终返回配送中心。一个站点在配送任务中只能服务 一次。

数学模型

配送中心存在n个需求点， dij 是配送车辆从地点i到地点j 之间的距离，总共有P辆配送小车， 每辆配送小车的最大载重量为 Lmax。xijk等于0或1，为1时表示第k个车辆由i驶向j，yik表示第i个点由车辆k配送。

根据问题的描述，可以得到基于配送的最小成本建立数学模型为：

F1,F2分别是车辆成本和时间窗惩罚成本。

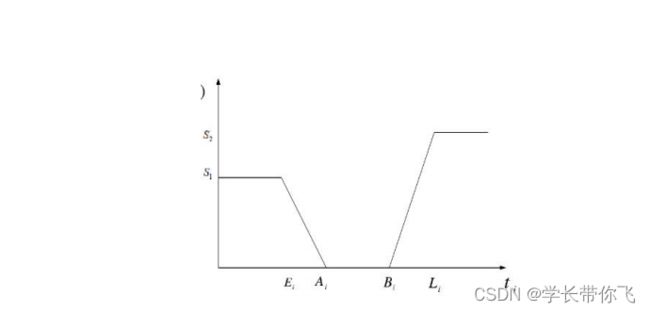
时间窗惩罚用一个图介绍：

横坐标是时间，纵坐标是惩罚成本

Ai和Bi是时间窗下限和上限，在时间窗内惩罚成本是0,当到达时间小于Ai且大于Ei或者大于Bi小于Li，惩罚成本线性变化，到达时间大于Li变成固定值s2，小于Ei变成固定值s1。

本文Ei=Ai-p*Ai，

Li=Bi+p*Ai，p是0到1之间的数。

第一个式子保证了车辆配送的总质量严格小于该车辆的最大载重质量，第二个式子保证了每个工序的配送只能由 1 辆车来完成，第三个和第四个式子保证了物料配送车辆从配送中心出发最后也要到返回到配送中心，最后一个式子表示派遣的配送车辆的数量 将不大于配送量之和与最大载重质量的商取整数。

算法设计

数据

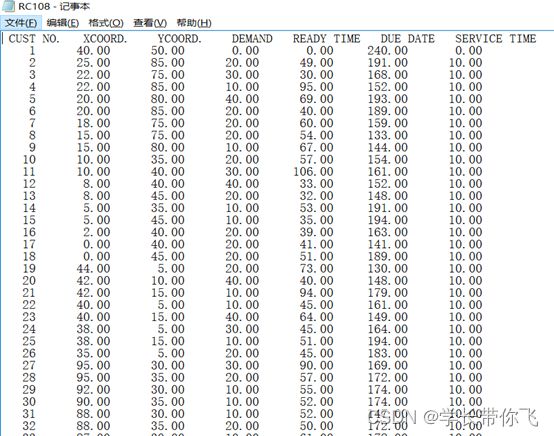
数据是RC108，文件里的text格式，截图如下：

第一行是配送中心，第二第三列是坐标，第4列是需求量，第五第六列是时间窗，最后一列是各个需求点的服务时间，文章不需要，去掉，配送中心也不需要时间窗，算法求解过程中没有涉及。数据是1个配送中心，100个需求点。

数据见网站：http://web.cba.neu.edu/~msolomon/rc101.htm

数据处理

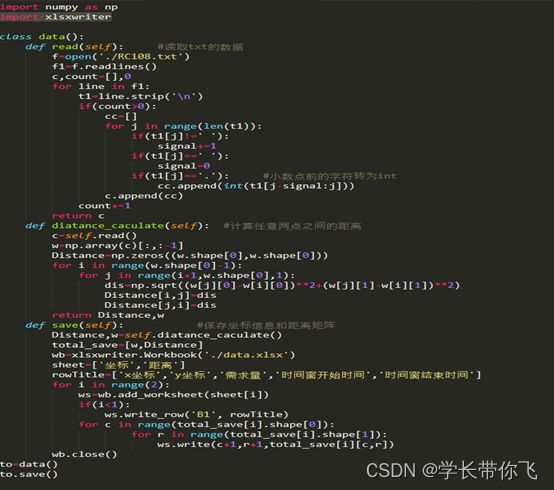
1、 从网站复制数据到txt,用python提取具体数据，提取的原则简单来说，就是截取每一行小数点前的数；

2、 提取出来数据，算101个点任意两个点之间的距离，保存为距离矩阵。

提取出来的都保存为excel,名字是data,具体的代码在text_solve。可以自行运行，机制是：如果有data.xlsx，则覆盖，没有则新创建一个。注意：如果存在data.xlsx且处于打开状态，程序会报错，关掉表格重新运行就可以了。

程序截图：

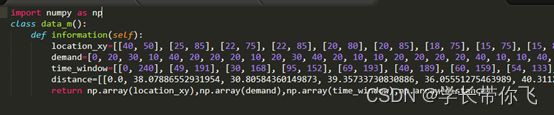
3、 为提高算法速度，已经把各个点的位置信息和距离矩阵保存到data.py里

截图如下：

编码解码及结果可视化

编码和解码

论文的编码是用1到100的数表示100个点的位置，任意打乱1到100的数后就是位置编码。遗传算法的编码生成采用这种方法。

一个可行编码如下：

[12, 5, 18, 56, 20, 45, 32, 85, 34, 46, 1, 35, 76, 29, 71, 97, 90, 39, 31, 60, 13, 53, 4, 33, 30, 57, 99, 37, 78, 16, 58, 96, 19, 91, 54, 22, 55, 94, 82, 52, 88, 8, 95, 87, 3, 89, 27, 49, 69, 38, 63, 24, 51, 79, 86, 70, 81, 23, 98, 14, 48, 61, 100, 9, 65, 80, 92, 44, 2, 93, 62, 7, 42, 6, 66, 41, 74, 84, 68, 15, 77, 72, 67, 36, 25, 17, 73, 28, 40, 50, 64, 26, 10, 83, 47, 75, 21, 43, 11, 59]

1、 根据位置读出各个点的需求量，如上面的12,5,18的需求量分别是40,40,20；

2、 用车的载重去匹配需求量，如果车的载重是80，那么18就换到下一辆车，得到该辆车路线0-12-5-0，注意：位置编码也读出车辆的配送顺序；

3、 依次类推，直到所有需求点都被车辆匹配完。

4、 根据路线，速度已知，距离已知，时间窗已知，就可以算出每辆车的配送成本和时间窗惩罚成本，解码完成。

代码如下：

def decode(self,road):
    global location_xy
    da=data_m()
    location_xy,demand,time_window,distance=da.information()
    car_road,car_p,car_s,car_time=[],[],[],[]
    car_road,car_p,car_s,car_time=[],[],[],[]
    time,car_code,car_demand,car_window,car_distance,car_un=[],[],[],[],[],[]
    signal=-1
    window_low=[]

    for i in range(road.shape[0]):
        loc_index=int(road[i])
        if(i<1)or(demand[loc_index]>car_load) : #当是第一个需求点或车辆的剩余载重小于需求量
            if(i>0):                            #当车辆的剩余载重小于需求量
                car_dis+=distance[loc_index,0]
                time_car+=distance[loc_index,0]/self.car_v
                time.append(time_car)
                car_time[signal].append(time_car)  #保存该车辆的累积运行时间
                car_p.append(p)                    #保存该车辆的时间窗惩罚成本
                car_s.append(car_dis)              #保存该车辆的路程
                
                car_road[signal].append(0)          
                car_window[signal].append(0)
                car_distance[signal].append(car_dis)
                car_un[signal].append(0)
            car_load=self.load_max
            car_road.append([0])
            car_window.append([0])
            car_time.append([0])
            car_distance.append([0])
            car_un.append([0])
            signal+=1                               #一辆车装完后换下一辆     
            car_dis=0                               #初始化每辆车的路程为0
            time_car=0                              #初始化每辆车的时间为0
            p=0                                     #初始化每辆车的时间窗惩罚成本为0
        car_load-=demand[loc_index]                 #每辆车的剩余载重更新
        car_road[signal].append(loc_index)
        car_code.append(signal)
        sig=car_road[signal][-2]
        svg=car_road[signal][-1]
        dis=distance[sig,svg]                       #计算每个需求点和上一个需求点的距离

        time_car+=dis/self.car_v                            #更新每辆车的运行时间
        car_dis+=dis                                #更新每辆车的路程                               
        car_distance[signal].append(car_dis)
        car_demand.append(demand[loc_index])
        car_window[signal].append(time_window[loc_index])
        car_time[signal].append(time_car)

        Ai=time_window[loc_index,0]                 #时间窗惩罚成本的各种参数
        Bi=time_window[loc_index,1]
        window_low.append(Ai)
        Ei=Ai-self.pi*Ai
        Li=Bi+self.pi*Ai
        if(time_car<=Ei):
            loss=self.s1
            car_un[signal].append(1)
        if(time_car>Ei)and(time_car<=Ai):
            loss=(self.s1/(Ai-Ei))*(Ai-time_car)
            car_un[signal].append(0)
        if(time_car>Ai)and(time_car<=Bi):
            loss=0
            car_un[signal].append(0)
        if(time_car>Bi)and(time_car<=Li):
            loss=(self.s2/(Li-Bi))*(time_car-Bi)
            car_un[signal].append(0)    
        if(time_car>Li):
            loss=self.s2
            car_un[signal].append(2)
        p+=loss                                     #更新每辆车的时间窗惩罚成本
        if(i==road.shape[0]-1):                     #最后一个点更新各个变量
            car_dis+=distance[loc_index,0]
            car_s.append(car_dis)
            car_window[signal].append(0)
            time_car+=distance[loc_index,0]/self.car_v
            time.append(time_car)
            car_p.append(p)
            car_road[signal].append(0)
            car_time[signal].append(time_car)
            car_un[signal].append(0)
            car_distance[signal].append(car_dis)
    Z=sum(car_s)+sum(car_p)
    return Z,[road,car_demand,car_code,window_low],[car_road,car_distance,car_window,car_time,car_un],[car_s,car_p]

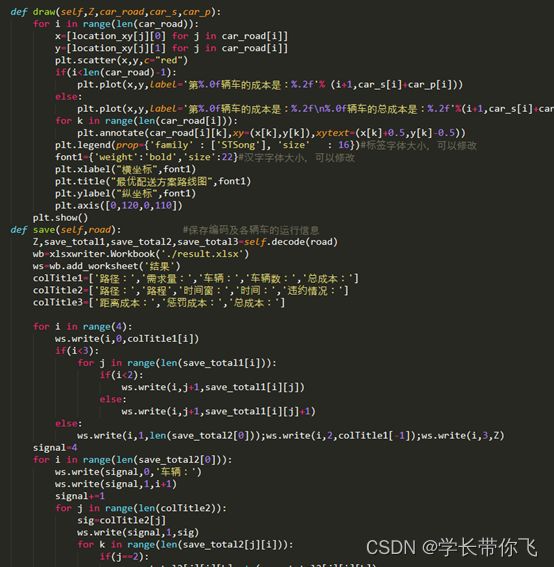
对于每辆车的运行路线，成本等结果，分别写了一个draw进行展示和save函数进行保存（保存逻辑同上）。具体的字体大小，布局等，可以自行在程序里调整，一个可行编码的效果和代码截图如下：

改进和声搜索算法

和声搜索算法

和声搜索算法是模仿音乐演奏的智能优化算法。简单来说，其把求解问题的解看做一个乐队演奏乐曲，不断调整乐器，直到得到满意的和声为止，几个关键变量：

1、和声库大小（ Harmony memory Size，HMS）：因为每个乐器演奏的音乐具有一定的范围，我们可以通过每个乐器的音乐演奏范围来构造一个解空间，然后通过这个解空间来随机产生一个和声记忆库，所以我们需要先为这个和声记忆库指定一个大小。

2、记忆库取值概率（Harmony memory considering rate, HMCR）：每次我们需要通过一定的概率来从这个和声记忆库中取一组和声，并且对这组和声进行微调，得到一个组新的和声，然后对这组新和声进行判别是否优于和声记忆库中最差的和声，这个判别使用的就是上面说的f(x)函数进行比较，所以，我们需要随机产生一个记忆库取值概率。

3、微调概率(Pitch adjusting rate, PAR)：上面已经说过，我们以一定的概率来在和声记忆库中选取一组和声，进行微调，这里指定的就是这个微调概率。

4、音调微调带宽 bw：上面说了会把从记忆库中取出的一组和声以一定的概率进行微调，这里指定就是这个调整幅度。

5、创作的次数 Tmax：这里指定的就是演奏家需要创作的次数，也就是上面整个调整过程需要重复多少次。

迭代逻辑：

（1）在[0，1]之间随机的产生一个变量rand1，并且将rand1与上面初始化的HMCR进行比较。

如果rand1小于HMCR，那么在上面初始化的和声记忆库中随机的得到一组和声
否则就在上面的解空间中随机的得到一组和声。
最终，就得到一组和声，如果这组和声是从和声库中得到的，就需要对这组和声进行微调，在[0，1]之间随机的产生一个变量rand2

如果rand2小于上面初始化的PAR，就需要以上面初始化的微调带宽bw来对和声进行调整，得到一组新和声
否则，不做调整
参考博客：https://blog.csdn.net/hp910315/article/details/50551420

对于本文的路径优化问题，用遗传算法的逆序变异替代上文的微调带宽bw，对解进行调整，下面先介绍一下逆序变异。

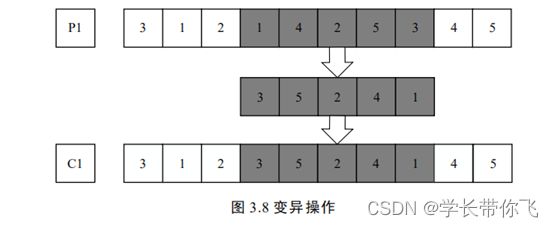
逆序变异

采用逆序变异：生成在编码长度内生成两个位置，对两个位置间的基因进行逆序变换。

一个逆序变换示意如下：

代码：

def Road_vara(self,W1,W2):       #路径的逆序变异
    W1,W2=np.array([W1]),np.array([W2])
    index1=random.sample(range(self.customers),2)
    index2=random.sample(range(self.customers),2)
    index1.sort(),index2.sort();
    L1=W1[:,index1[0]:index1[1]+1]
    L2=W2[:,index2[0]:index2[1]+1]
    W_all=np.zeros((2,W1.shape[1]))
    W_all[0],W_all[1]=W1[0],W2[0]
    for i in range(L1.shape[1]):
        W_all[0,index1[0]+i]=L1[0,L1.shape[1]-1-i]  #反向读取路径编码
    for i in range(L2.shape[1]):
        W_all[1,index2[0]+i]=L2[0,L2.shape[1]-1-i]  #反向读取路径编码
    return W_all[0],W_all[1]

算法步骤：

• 步骤1：随机初始多个路径编码，解码得到成本，当做和声库HMS

• 步骤2：如果随机数rand1小于HMCR，随机挑选HMS的一个个体，转入步骤3；否则另外随机生成一个新编码，转入步骤4

• 步骤3：如果rand2小于PAR，对挑选的个体进行逆序变异，得到新编码；否则不调整

• 步骤4：解码得到新编码的成本，如果成本小于和声库的最劣解（最大成本对应的解)，取代最劣解，否则不取代。

• 步骤4：判断是否达到创作次数Tmax，是的话输出结果，否则转到步骤1

代码：

def HS_total(self):
    Total_road=np.zeros((self.HMS,self.customers))
    Total_road1=np.zeros((self.HMS,self.customers))
    answer=[]
    result=[]
    signal=self.Tmax//100                
    for gen in range(self.Tmax):
        if(gen<1):
            for i in range(self.HMS):     #初始生成和声库
                road=np.arange(1,self.customers+1,1)
                np.random.shuffle(road)
                Total_road[i]=road
                Z,_,_,_=self.go.decode(road)
                answer.append(Z)
            result.append([gen,min(answer)])
            print('和声算法算法初始的成本:%.2f'%(min(answer)))
        r1,r2=np.random.rand(),np.random.rand()
        if r1<self.hcmr :                           #小于hcmr
            loc=np.random.randint(0,self.HMS,1)[0]  #从和声库随机挑选个体
            x=Total_road[loc]
            if r2<self.par :                        #小于par
                road_new=self.Road_vara(x)          #逆序变异生成新编码
            else:
                road_new=x                          #不小于par的话，不调整x
        else:
            road_new=np.arange(1,self.customers+1,1) #不小于hcmr，随机生成新编码
            np.random.shuffle(road_new)

        Z_new,_,_,_=self.go.decode(road_new)
        max_Z=max(answer)
        max_index=answer.index(max_Z)
        if Z_new<max_Z :                            #如果新编码的成本小于和声库的最大成本
            Total_road[max_index]=road_new          #取代最大成本对应的解
            answer[max_index]=Z_new
        Z1=min(answer)
        min_index=answer.index(Z1)
        result.append([gen+1,Z1])
        if ((gen+1)%signal==0)or(gen==self.Tmax-1):
            print('和声算法算法第%.0f次迭代的成本:%.2f'%(gen+1,Z1))
    return result,Total_road[min_index]

为避免print太多次造成的卡顿问题，每次对把Tmax分为100个时间段，每个时间段结束print一次。

结果

代码运行环境
windows系统，python3.6.0,第三方库及版本号如下：

numpy==1.18.5
matplotlib==3.2.1
xlsxwriter==1.4.3
xlrd==1.2.0

第三方库需要在安装完python之后，额外安装，以前文章有讲述过安装第三方库的解决办法。

主函数

设计主函数如下：

from hs import HS
from Road_decode import tool
import numpy as np
import matplotlib.pyplot as plt 
import time

if __name__ == '__main__':
    load_max=200                    #载重
    car_v=2                         #速度
    parm_p=[200,400,0.3]            #惩罚成本各参数,s1,s2和违反约束比例
    customers=100                   #100个需求点
    go=tool(load_max,car_v,parm_p)  #解码模块

    Tmax,HMS=10000,10           #创作次数和和声库大小
    parm_hs=[0.95,0.1]          #和声算法的记忆库取值概率HMCR和微调概率PAR

    start = time.clock() 
    to=HS(customers,Tmax,HMS,parm_hs,go)
    result,road=to.HS_total()               #算法迭代结果
    end = time.clock()
    t2=end-start
    print('花费时间：%.2f 秒'%(t2))
    
    file='./result_hs.xlsx'
    go.save(road,result,file)    #保存
    Z,save_total1,save_total2,save_total3=go.decode(road)
    car_road,car_s,car_p=save_total2[0],save_total3[0],save_total3[1]
    go.draw(Z,car_road,car_s,car_p)#画图
            
    result=np.array(result).reshape(len(result),2)
    plt.plot(result[:,0],result[:,1])
    font1={'weight':'bold','size':22}#汉字字体大小，可以修改
    plt.xlabel("迭代次数",font1)
    plt.title("成本变化图",font1)
    plt.ylabel("成本",font1)
    # plt.legend(prop={'family' : ['STSong'], 'size'   : 16})#标签字体大小，可以修改
    plt.show()

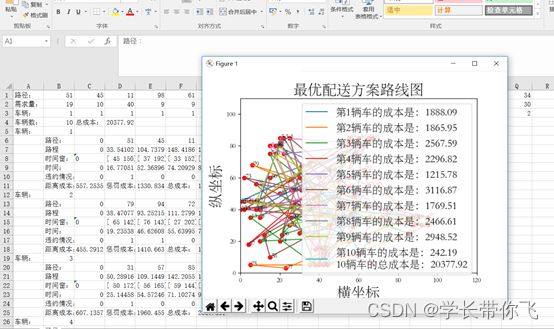
运行结果

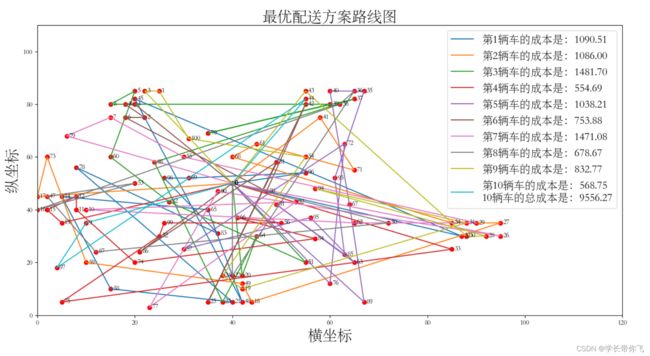
结果如下：

路线图如下：

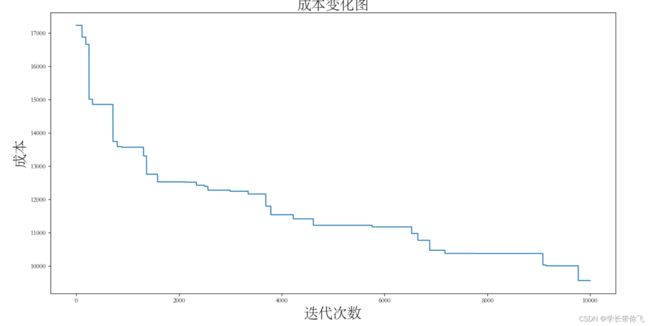
成本随迭代次数的变化图如下：

excel结果截图如下：

代码

有4个代码,data太大没有展示，原始数据及处理代码可以看上一篇推文。

演示视频：

路径优化丨改进和声算法求解CVRPTW问题

完整算法源码+数据：见下方微信公众号：关注后回复：路径优化

# 微信公众号：学长带你飞
# 主要更新方向：1、车辆路径问题求解算法
#              2、学术写作技巧
#              3、读书感悟
# @Author  : Jack Hao

公众号二维码：