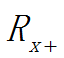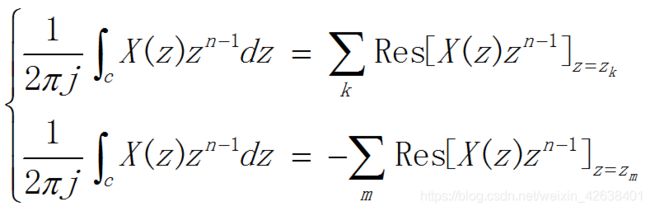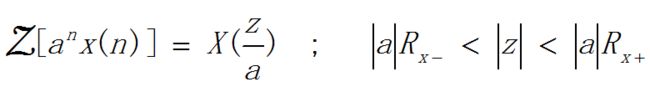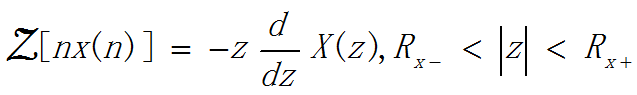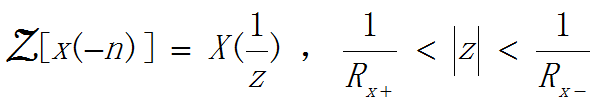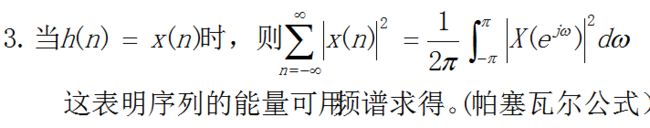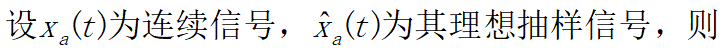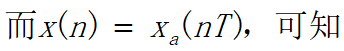Z变换

 

信号与系统的分析方法

可以分为两大类：时域分析和变换域分析

1.时域分析法：

（1）连续时间信号与系统：信号的时域运算、分解，微分方程的经典解法；卷积积分

（2）离散时间信号与系统：序列的变换与运算，差分方程的经典求解；卷积和

2.变换域分析法：

（1）连续时间信号与系统：（频域分析）傅里叶变换、（复频域分析）拉普拉斯变换

（2）离散时间信号与系统：（频域分析）序列的傅里叶变换DTFT，离散傅里叶变换DFT、（复频域分析）z变换

---

阿贝尔定理 

1.如果幂级数在点x0处（x0不等于0）收敛，则对于适合不等式|x|<|x0|的一切x使这幂级数绝对收敛。

2.反之，如果幂级数在点x1处发散，则对于适合不等式|x|>|x1|的一切x使这幂级数发散。

---

 留数定理 

在复分析中，留数定理是用来计算解析函数沿着闭曲线的路径积分的一个有力的工具，也可以用来计算实函数的积分。它是柯西积分定理和柯西积分公式的推广

 当γ是若尔当曲线（平面上一条简单的曲线）

---

 Z变换（z-transformation）（离散时间信号的复频域分析）：可将离散时间序列变换为在复频域的表达式，可将差分方程转化为代数方程。它在离散时间信号处理中的地位，如同拉普拉斯变换在连续时间信号处理中的地位。离散时间信号的Z变换是分析线性时不变离散时间系统问题的重要工具，在数字信号处理、计算机控制系统等领域有着广泛的应用。

数学上，Z变换也可以看作是一个洛朗级数。

Z变换 将离散系统的时域数学模型——差分方程转化为较简单的频域数学模型——代数方程，以简化求解过程的一种数学工具。离散信号系统的系统函数（或者称传递函数）一般均以该系统对单位抽样信号的响应的Z变换表示。

（双边）Z变换表达式：

单边Z变换：只对右边序列进行Z变换

收敛域 region  of  convergence  ( ROC )

 Z变换的存在的充分必要条件是：级数绝对可和。使级数绝对可和的成立的所有Z值称为Z变换域的收敛域。由Z变换的表达式及其对应的收敛域才能确定原始的离散序列。

特点

（1）收敛域是一个圆环，有时可向内收缩到原点，有时可向外扩展到∞，只有的收敛域是整个Z平面；

（2）在收敛域内没有极点，X(Z)在收敛域内每一点上都是解析函数。

 

分类

（1）有限长序列

当时，收敛域包括

当时，收敛域包括

（2） 右边序列

第一项是有限长序列，收敛域为，第二项为z的负幂级数，根据阿贝尔定理，收敛域为Rx-<|z|≤∞

两者都收敛的域为Rx-<|z|≤∞，Rx-为最小收敛半径

因果序列（一种重要的右边序列）

收敛域为 

（3）左边序列

 第二项为有限长序列，收敛域为 ，第一项为z的正幂级数，根据阿贝尔定理，其收敛域为

 为最大收敛半径，

（4）双边序列

第一项为右边（因果）序列，收敛域为 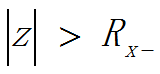，第二项为左边序列，收敛域为

当Rx- 

 

Z逆变换 

已知Z变换X(Z)求对应的离散时间序列x[n]称为Z变换的逆变换，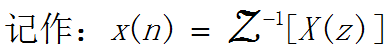 

 

c为环形解析域内环绕原点的一条逆时针闭合单围线

求解方法 

 （1）留数法（ residue method）(围线积分法)

由留数定理（ residue theorem）可知，

即在围线C内所有极点上留数值的总和

或者在围线C外所有极点上留数值的总和

（2）部分分式法(partial fraction expansion method )(用到海维赛展开定理) 

例题1：求 ，的z逆变换

解

Z变换的性质

 1.线性

收敛域为两者重叠部分

2. 序列移位

3.Z域尺度变换（乘以指数序列）

 4.序列的线性加权（Z域求导数）

5.共轭序列

6.翻折序列

7.初值定理

8.终值定理

9.有限项累加特性

10.序列的卷积和（时域卷积定理）

11.序列相乘（Z域卷积定理）

 
其中,c是在变量v平面上，X(z/v),H(v)公共收敛域内环原点的一条逆时针单封闭围线。

12.帕塞瓦定理 

则

其中“*”表示复共轭，闭合积分围线c在公共收敛域内。 

几点说明：

 汇总表

常用变换对

z变换与傅氏变换，拉式变换的关系

1.z变换与拉式变换的关系

（1）理想抽样信号的拉式变换

对其求拉式变换

（2）s平面与z平面的映射关系

 

这就是说，z 的模 只与s的实部相对应；

z的相角只与s的虚部Ω相对应 。

1）.z的模r与s的实部σ的关系

σ=0，对应s平面的虚轴，r=1，即z平面单位圆；

σ>0，对应s右半平面，r>1,即z平面单位圆以外；

σ<0，对应s左半平面，r<1,即z平面单位圆以内；

2）z的相角ω与s的虚部虚部Ω的关系（ω=ΩT）

 Ω=0，对应s平面实轴，ω= 0，z平面正实轴

Ω=Ω0(常数)，s:平行实轴的直线，ω=Ω0T,z:始于原点的射线

s平面到z平面的映射是多值映射

2.z变换和傅氏变换的关系

连续信号经理想抽样后,其频谱产生周期延拓，即

傅氏变换是拉氏变换在虚轴s=jΩ上的特例,因此

序列在单位圆上的z变换称为序列的傅里叶变换，

它等于理想抽样信号的傅里叶变换，反映了信号的频谱。