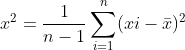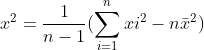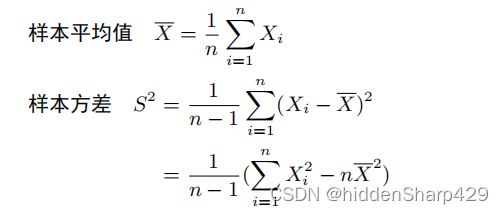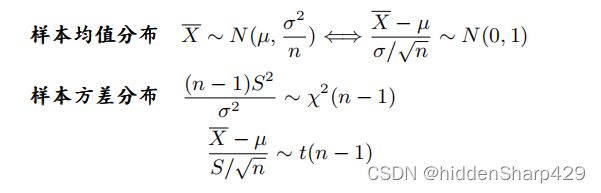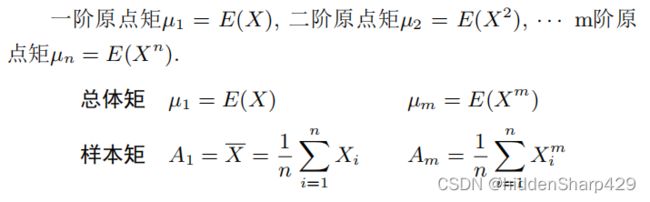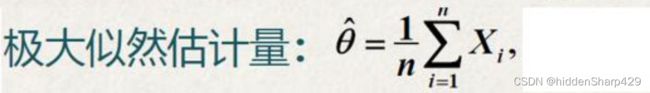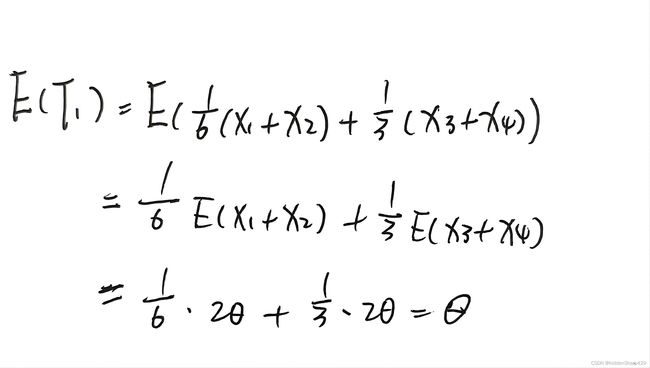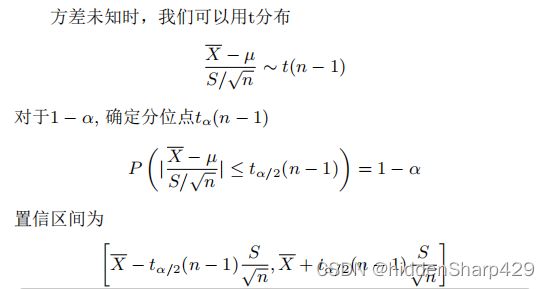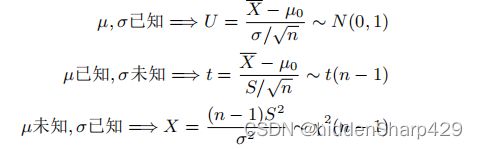郝志峰《概率论与数理统计》期末复习笔记（火速持续更新中~）
目录
前言
第一章 概率论的基础概念
知识大纲
随机试验
随机事件
事件概率
等可能概率模型
第五章 多维随机变量及其分布
知识大纲
二维随机变量
边缘分布和条件分布
相互独立的随机变量
两个随机变量的函数分布
第六章 样本及抽样分布
知识大纲
总体与样本
统计量
统计三大抽样分布
标准正态分布 X~N (0,1)
卡方分布
t分布
样本均值和方差
第七章 参数估计
知识大纲
点估计
矩估计法
极大似然估计法
估计量的评选标准
区间估计
正态分布总体均值和方差的区间估计
均值区间估计
方差置信区间
第八章 假设检验
知识大纲
小概率事件和否定域
已知期望方差的假设检验
未知期望方差的假设检验
题外话
前言
所用课本是郝志峰老师所编著的《概率论与数理统计》本篇文章主要是以核心知识点为主，为穿插部分习题，以此来达到学习的目的。所用课件是老师上课的课件。你准备好了吗？~
第一章 概率论的基础概念
知识大纲
1.随机试验
2.随机事件
3.事件概率
4.等可能概率模型
随机试验
1.可以在相同的条件下重复进行
2.可能结果不止一个，能事先明确所有可能结果
3.测试前不能确定哪一个结果会出现。
随机事件
由样本空间S、样本点、事件、基本事件组成
样本空间S：随机试验的所有可能结果组成的集合
样本点：样本空间的元素
事件：样本空间的子集
基本事件：由一个样本点组成的单点集
答：A是基本事件，B不是基本事件。B是多个样本点所组成的集合故不满足单点集的概念
从单个随机事件的结果来看有三种情况
1.当且仅当随机事件中的一个样本点发生时事件发生（如上题当掷骰子掷出3点的时候事件B发生）
2.必然事件（如上题，掷出点数小于7点）
3.不可能事件（如上题，掷出点数为7点）
从两个或者多个随机事件
事件之间的关系有
除此之外还有互斥事件和对立事件
事件概率
这么说有点抽象，那举出一个例子来体会一下
这题不难，但很多同学做这道题都做不对（我之前也写错了）
解析：首先要弄清楚，小明喜欢这两本书是不是独立事件。0.4×0.5=0.2≠0.3 ，故这不是独立事件，喜欢两本书是有关联的，你不能用独立事件的公式带进去。那么我们应该怎么算呢？设P(A)为小明喜欢第一本书的概率，P(B)为小明喜欢第二本书的概率。由题意可知P(A)=0.5;P(B)=0.4。他有一本书是喜欢的事件为C事件，则P(C)=P(A U B)=P(A)+P(B)-P(AB)=0.5+0.4-0.3=0.6，那么C事件的相反事件就是两本书都不喜欢的事件，则答案为1-0.6=0.4
等可能概率模型
这个高中应该是有学过的，在这我就不再赘述了，只需要记住主要的公式就好了。
注意：在这里知识点出题重点在于放回和不放回
那么来道题来试试吧
解析：总共5双鞋子也就是10只鞋子，题目的意思是从10只里面取4只。对于第一个问题，我们可以这样想：4只鞋子刚好为2双，那么满足条件的事件就等于我从5双鞋子里抽出2双来的事件数量
。总的基本事件数量是
，故概率就等于它们两个相除。对于第二个问题，我们可以这样想：先从5双鞋中抽出4双来也就是
,因为每双鞋子分为左右脚，所以还要乘
，故概率就等于×
再除总的基本事件数量。对于第三个问题，我们可以这样想：先从5双中抽1双出来，这时候我们还剩下两只鞋要抽，从剩下4双鞋中选2双出来再选择左右脚。也就是
，再将其于总的基本事件相除就好了
第五章 多维随机变量及其分布
知识大纲
二维随机变量
边缘分布和条件分布
相互独立的随机变量
两个随机变量的函数分布
第六章 样本及抽样分布
知识大纲
1.总体与样本
2.统计量
3.统计三大抽样分布
4.样本均值和方差
总体与样本
首先我们要了解一些相关的概念
- 总体：研究对象的全体
- 个体：总体中的每一个成员
- 容量：总体里包含个体的数量
一般来说总体的分布是未知的，但是知道其分布是服从何种分布，我们从总体中抽出若干个个体的过程就叫抽样，抽取的部分个体称为样本
| 直观理解 | 数学本质 | |
| 总体 | 研究对象的全体 | 随机变量X |
| 个体 | 组成总体的每个样本单位 | 与总体同分布的某个随机变量 |
| 样本 | 总体抽出的n个个体 | n个随机变量，X1、X2...Xn |
| 简单随机抽样 | 重复、独立抽取所得样本 | 要求X1..Xn互相独立，且与总体同分布 |
统计量
统计量的定义：不含任何未知参数的样本的函数称为统计量。它是完全由样本决定的量
| 常见的统计值 | 常见的观察值 |
| 样本平均值 |
 |
| 样本方差
|
|
经验分布函数，其中s(x)为x1,x2,x3....xn中不大于x的随机变量的个数
例子：设F有样本值1，1，2，其经验分布函数为什么
解析：
统计三大抽样分布
标准正态分布 X~N (0,1)
性质：E(X) = 0 , D(X) = 1
标准正态分布比较简单在此就不做过多的赘述了
卡方分布
什么是卡方分布？
X1,X2.......Xn相互独立，且均满足正态分布N（0，1），则有
所服从的分布为自由度为n的
分布，记作~（n）
卡方分布的重要性质
题目：
解析：令
为m，
为n，当m和n互相独立时候才有m+n ~ ，故该题需要令b = 0，来切断联系。所以答案选C
t分布
什么是t分布？
t分布的重要性质
样本均值和方差
假如现在我从一个已知总体分布为正态分布的总体中抽出了n个样本（总体均值u和方差已知），那么样本均值和方差为
我们常用到的样本均值分布和样本方差分布
注意到了在求样本方差的时候如果总体的方差已知就用卡方分布，反之则用t分布
下面我们用一道题来体会一下上面这句话是什么意思
题目：设总体X服从正态分布N（12，
）抽取容量为25的样本，求得样本均值
大于12.5的概率。如果
（1）已知 =12；
（2）未知，但已知方差样本
= 5.57
解析：
第七章 参数估计
知识大纲
1.点估计
1.1矩估计法
1.2极大似然估计法
2.估计量的评选标准
3.区间估计
4.正态分布总体均值和方差的区间估计
4.1均值区间估计
4.2方差置信区间
点估计
矩估计法
一般来说题目只涉及一阶的情况 由大数定理我们可以得出，当样本数量n充分大的时候，样本矩就近似于总体矩
极大似然估计法
值得注意的是极大似然估计量的式子与样本矩的式子一样！ 极大似然估计量是先通过似然函数取对数，再求导数，最后解导数等于零时极大似然估计量的式子。
估计量的评选标准
什么是无偏估计？
理解了什么是无偏估计后我们来做一道题
解析：即需证E(T1) = E(T2) = θ
这个证明较为简单，下面只列出T1的证法，T2同理
当算出E(T2) = θ 时我们又遇到了一个问题哪个无偏估计更好点呢？对于这个我们要看方差
解析：
再来一道题练习，这道题要用到之前学过的知识
解析：（我这写的比较乱，可能不太看得清）
区间估计
什么是区间估计呢？
假如估计全校同学的身高符合正态分布X~N（u，0.1）。我从总体中抽出若干个样本，假如我抽五个，它们分别是：1.65、1.67、1.68、1.78、1.69
那我估计u = 1.68 （点估计）
我估计u∈ [1.57,1.86]（区间估计）
在区间估计中有一个很重要的概念，那就是置信水平（也可称之为置信度）。
正态分布总体均值和方差的区间估计
均值区间估计
在这里设题一般分为两种情况，第一种是已知正态分布的方差，第二种是未知正态分布的方差。两种情况一般让你求的是总体均值u置信度为1-a的置信区间
下面是基本的解法
（注意：这里因为你是从总的正态分布中取样本出来，所以样本的均值
和它的样本方差S已知）
同样的未知方差也有其基本公式
现在来道题测试一下
首先判断是第二种情况，正态分布总体方差未知的情况，要用t分布。已知自由度为25，样本均值为170，样本标准差为25，代入公式。
方差置信区间
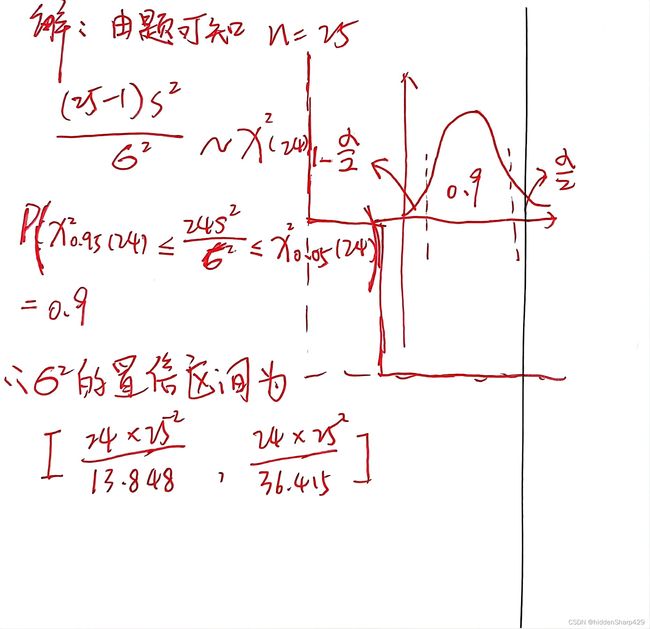
这里相比于求均值的置信区间的方法，大部分是类似，但是满足的分布是X^2分布，并且X^2分布的图像不像是t分布是关于y轴对称的，故在下面概率P的关系式有些许不同！！
这里也来道题来试试
解析：
最后的答案是（12.177，19.747）
现在把求均值和方差的置信区间综合起来做一道题
答案我放在下面了
第八章 假设检验
知识大纲
1.小概率事件和否定域
2.已知期望方差的假设检验
3.未知期望方差的假设检验
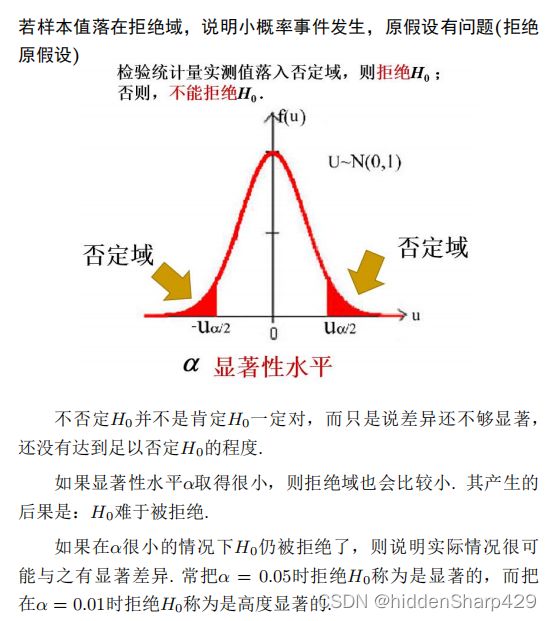
小概率事件和否定域
数学上，把发生概率小于0.05的事件称为小概率事件，小概率事件在一次试验中几乎不可能发生，除非我们原先猜测的分布错了，不然很难出现小概率事件。
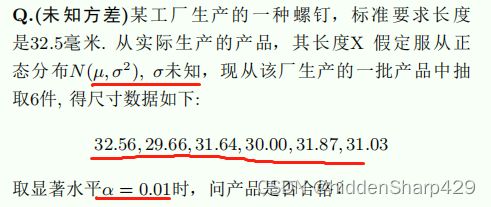
已知期望方差的假设检验
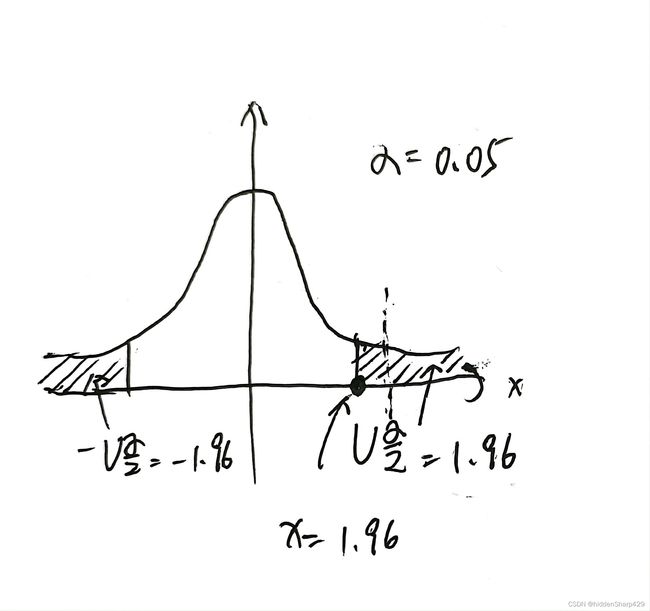
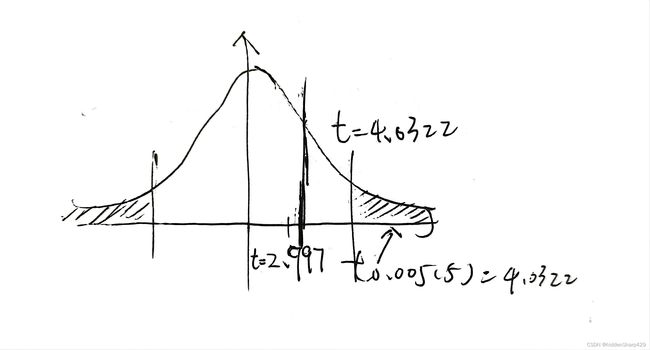
由这题题干我们可以得知我们已知的是样本平均值、总体正态分布的方差、抽样的数量。现在要求我们证明的是，这个样本平均值是否是落在显著水平α为0.05正态分布的否定域上的，因此为了方便起见，我们先假设μ=32.5，观察是否数据平均值是落在否定域上的。
解析：
也就是说当样本均值为36.5时，它落在了总体均值为32.5的否定域上这个事件发生的概率极小，故原先的假设即总体均值为32.5不成立，所以能推出来，这批产品不合格
此外与产品合格的假设检验相类似的是药物有效的假检验 ，主要的区别在于原假设的设置！！
未知期望方差的假设检验
那么相比于已知期望方差的假设检验，未知期望方差的假设检验该怎么做呢？
答案很简单，那就是服从的分布不同！
解析：
样本均值落在了否定域外的，故原假设是成立的，因此这批产品是合格的！
那我们现在来一道比较综合的假设检验例题看看
解析：
题外话
这篇文章会持续更新，记录学习过程中发现以及解决的问题！如果有什么疑问欢迎大家在底下留言讨论！我们一起进步拿offer！