论文代码复现-深度补全算法

论文代码复现-深度补全算法

注：如果你有论文复现的需求可在文末留言

论文名称：A new method for inpainting of depth maps from time-of-flight sensors based on a modified closing by reconstruction algorithm
该文章采用传统的图像处理方法对深度图中缺失的区域进行补全

算法流程

首先是输入一张深度图，然后判断深度图中的缺失噪声点数据，如果存在噪声点将执行改进后的算法2，并根据指定的传播条件对缺失区域的进行填充。

可执行代码链接 https://download.csdn.net/download/qq_43627520/84278465

该算法流程图的运行代码

# 论文主函数
    def MCrB_main(self):
        lmd = 1
        # 执行一次闭运算
        self.g1 = cv2.morphologyEx(self.depth.copy(), cv2.MORPH_CLOSE, self.kernel,iterations=lmd)
        # 判断噪声数
        while len(self.g1[~(self.g1>0.)])>0:
            print("size",len(self.g1[~(self.g1>0.1)]))
            # 执行一次膨胀运算
            self.depth_d = cv2.dilate(self.depth.copy(),self.kernel,iterations=lmd)
            # 调用R_Close
            self.g2 = self.R_Close2(self.depth.copy(),self.depth_d,iterations=lmd)
            # 调用比较g_comparator
            self.g1 = self.g_comparator(self.g1,self.g2)
            lmd +=1
        print(lmd)
        self.depth[~self.n] = self.g1[~self.n]
        # self.res = cv2.normalize(self.g1.copy(),None,0,255,cv2.NORM_MINMAX)
        # self.depth = cv2.normalize(self.depth.copy(),None,0,255,cv2.NORM_MINMAX)
        return self.g1,self.depth

关于该文中太多的原理就不做介绍，直接开始论文中核心算法的复现工作。

算法1：顺序对偶重构算法，该方法是引用了其他论文中的算法框架。

该算法主要使用8个领域点对P点进行处理

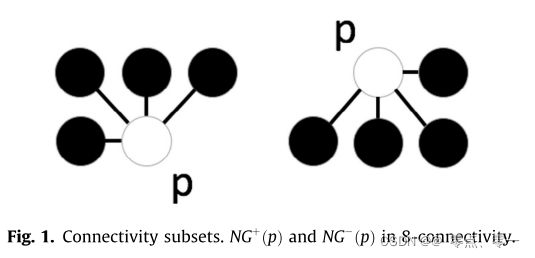
对算法1的改进后得到算法2

算法2函数的框架代码如下

1、在这个地方我写了三个函数，分别是 _Close()、R_Close、R_Close2；
2、_Close()：用于对写的重构形态学闭合函数进行验证，判断算法过程是否正确；
3、R_Close、R_Close2作为方法中调用的子类函数，其中对R_Close进行了稍微的调整；论文中的原方法是R_Close2函数中的内容。

    # 论文改进的重构形态学闭运算
    # R*(f,g)
    def _Close(self,f,J,iterations=1):
        for i in range(iterations):
            aux = J.copy()
            flag = True
            while flag:
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(1, f.shape[0]+1):
                    for j in range(1, f.shape[1]+1):
                        Jp = [J_[i - 1, j - 1], J_[i - 1, j], J_[i - 1, j + 1], J_[i, j - 1], J_[i, j]]
                        # J[i,j] = max(depth[i,j],aux)
                        J[i - 1, j - 1] = max(min(Jp), f[i - 1, j - 1])
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(1, f.shape[0] + 1):
                    for j in range(1, f.shape[1] + 1):
                        Jp = [J_[i, j], J_[i, j + 1], J_[i + 1, j - 1], J_[i + 1, j], J_[i + 1, j + 1]]
                        # J[i, j] = max(depth[i, j], aux)
                        J[i - 1, j - 1] = max(min(Jp), f[i - 1, j - 1])
                diff = J - aux
                if np.max(diff) == 0 or 255:
                    flag = False
        return J
    def R_Close(self,f,J,iterations=1):
        for i in range(iterations):
            aux = J.copy()
            flag = True
            while flag:
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(1,f.shape[0]+1):
                    for j in range(1,f.shape[1]+1):
                        Jp = [J_[i - 1, j - 1], J_[i - 1, j], J_[i - 1, j + 1], J_[i, j - 1], J_[i, j]]
                        # aux = min(Jp)
                        J[i-1, j-1] = self.K(min(Jp),f[i-1,j-1])
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(1,f.shape[0]+1):
                    for j in range(1,f.shape[1]+1):
                        Jp = [J_[i, j], J_[i, j + 1], J_[i + 1, j - 1], J_[i + 1, j], J_[i + 1, j + 1]]
                        J[i-1, j-1] = self.K(min(Jp), f[i-1, j-1])
                diff = J-aux
                if np.max(diff)==0 or 255:
                    flag = False
        return J
    def R_Close2(self,f,J,iterations=1):
        for i in range(iterations):
            aux = J.copy()
            flag = True
            while flag:
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(f.shape[0]):
                    for j in range(f.shape[1]):
                        Jp = [J_[i, j], J_[i, j+1], J_[i, j+2], J_[i+1, j], J_[i+1, j+1]]
                        aux = min(Jp)
                        J[i, j] = self.K(min(Jp),f[i,j])
                J_ = np.pad(J.copy(), (1, 1), mode='edge')
                for i in range(f.shape[0]):
                    for j in range(f.shape[1]):
                        Jp = [J_[i+1, j+1], J_[i+1, j + 2], J_[i+2, j ], J_[i+2, j+1], J_[i + 2, j + 2]]
                        aux = min(Jp)
                        J[i, j] = self.K(min(Jp), f[i, j])
                diff = J-aux
                if np.max(diff)==0 or 255:
                    flag = False
        return J

用例测试

文中中对该算法的验证给出了一个测试用例，我也用该用例对_Close()函数进行验证，验证程序如下，其中我们计算的结果与文中给出的用例结果一致，表明本文复现的重构形态学闭运算代码是正确的。

测试代码：

T = np.array([
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 7, 7, 7, 7, 7, 9],
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 7, 0, 0, 0, 7, 9],
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 7, 0, 5, 0, 7, 9],
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 7, 0, 0, 0, 7, 9],
         [9, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 5, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 0, 0, 0, 0, 0, 0, 0, 7, 9, 9, 9, 9, 9],
         [9, 7, 7, 7, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9],
         [9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
         ],dtype=np.float32)

def test_paper(Mcbr):
    KERNEL_3 = np.ones((3, 3))
    # 原始变化
    Mcbr = Mcbr(T.copy())
    b = cv2.dilate(T.copy(),KERNEL_3,iterations=1)
    print("b\n",b)
    c = Mcbr._Close(T.copy(),b)
    print("c\n",c)
    d = cv2.dilate(T.copy(),KERNEL_3,iterations=2)
    print("d\n",d)
    e = Mcbr._Close(T.copy(),d,iterations=2)
    print("e\n",e)
    # 论文方法
    f = cv2.dilate(T.copy(),KERNEL_3,iterations=1)
    print("f\n",f)
    g = Mcbr.R_Close(T.copy(),f)
    print("g\n",g)
    h = cv2.dilate(g.copy(),KERNEL_3,iterations=2)
    print("h\n",h)
    i = Mcbr.R_Close(T.copy(),h,iterations=2)
    print("i\n",i)
    g[~(g>0)] = i[~(g>0)]
    print("j\n",g)
    print(Mcbr.MCrB_main())

算法3 定义的传播条件

# 定义传播条件 conditional propagation k
    def K(self,aux,Ip):
        list = [Ip,aux]
        propagated = 0
        for x in list:
            if x>propagated and propagated<255:
                propagated = x
        return propagated

算法4 对比功能

    def g_comparator(self,g1,g2):
        non_1 = (self.g1 > 0)
        self.g1[~non_1] = g1[~non_1]
        non_2 = (self.g1 > 0)
        self.g1[~non_2] =  g2[~non_2]
        return self.g1

测试结果

对于其他测试图像，我们修复的结果与文中的结果一致。

但是对于该深度图

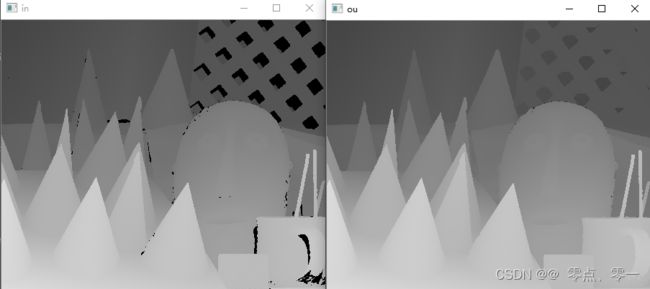
错误1：测试了原文中所使用的图像后，却得不到与原文中相同的结果，只对缺陷中前半部分数据进行了修复。

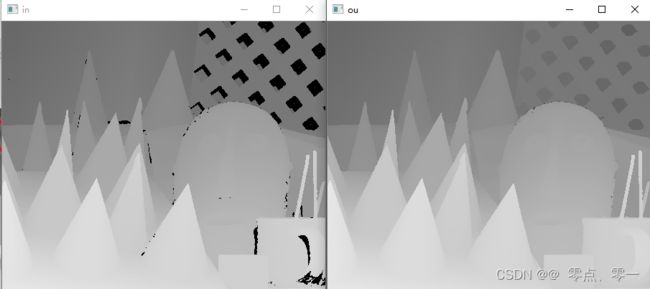
随后我们对输入图像进行调整；此时可以得到与论文中相同相近似的结果。

如果您找到出现该现象的原因，非常欢迎您来指正，在此感谢！

结论：该方法可以对深度图中缺失的区域进行有效的补全，但缺陷就是速度太慢。

可执行代码链接 https://download.csdn.net/download/qq_43627520/84278465

参考文献

【1】Garduño-Ramón M A, Terol-Villalobos I R, Osornio-Rios R A, et al. A new method for inpainting of depth maps from time-of-flight sensors based on a modified closing by reconstruction algorithm[J]. Journal of Visual Communication and Image Representation, 2017, 47: 36-47.