多层神经网络 ——小批量梯度下降法
在前面的课程中,我们知道为了实现非线性分类的任务,需要使用多层神经网络,多层神经网络的损失函数不再是凸函数,而是一种比较复杂的不规则函数,这类函数求导数非常困难,在求解极值问题时很难通过计算得到解析解,因此,通常采用梯度下降法得到数值解。
梯度下降法有着三种不同的形式,分别是批量梯度下降、随机梯度下降和小批量梯度下降。
下面,就来详细的介绍下这三种方法。为了便于理解,我们以一元线性回归为例,下图为一元线性回归的平方损失函数,

这里的 n 表示样本数。
批量梯度下降法
在这三种形式中,批量梯度下降法是最原始的形式。每一次迭代更新权值时,都使用所有样本来计算偏导数。

采用这种方法由所有样本确定梯度方向,可以保证每一步都是准确地向着极值点的方向趋近,收敛的速度最快,所需要的迭代次数最少,当目标函数是凸函数时,一定能够收敛于全局最小值,如果目标函数是非凸函数,则会收敛到某个局部极小值点。
对所有样本的计算,可以利用向量运算进行并行计算来提升运算速度。
对于小规模数据集,通常采用这种批量梯度下降法进行训练,例如,在前面介绍的所有例程中使用的都是这种方法,但是在神经网络和深度学习中,样本的数量往往非常大,可能有数万个或者数百万个,甚至上亿个样本,每个样本中,属性的个数也可能非常的大,采用批量梯度下降法,在每一步迭代时,都需要用到所有的样本,计算量可能会大的惊人,即使使用向量运算,也需要花费大量的时间。
例如,数据集中有 20 万个样本,那么每次迭代都需要使用这 20 万个样本进行计算才能对参数进行一次更新,假设达到极小值需要进行10次迭代,那么就一共需要200万次计算,才能达到收敛。
其实,在大规模数据集中,通常会有大量冗余数据,也没有必要使用整个训练集来计算梯度,因此,批量梯度下降法并不适合大规模数据集。为了实现更快的计算,可以使用随机梯度下降法。
随机梯度下降法
在这种方法中,每次迭代时只使用一个样本来训练模型,也就是说每次只使用一个样本去计算代价函数的梯度并迭代更新模型的参数,使模型的输出值尽可能逼近这个样本真实的标签值。
当训练误差足够小时,结束本次训练,再输入下一个新的样本,显然使用前面样本训练出的网络参数,不一定能够使得后面的新样本误差最小,所以这个新样本需要再重新训练网络,这个样本训练结束之后,再输入下一个样本,再次训练网络,直到使用所有样本训练一遍为止,这个过程也被称为一轮。
例如,对于一个有20万个样本的数据集,训练一轮就是依次使用这 20 万个样本训练一遍网络。因为每次训练只使用了一个样本,因此每次训练速度非常快,可以想到在训练一轮之后,整个网络的模型参数对最后一个样本的误差达到了最小。但是对前面的样本就不好说了。因为后面样本调整了网络参数,又可能会使得前面样本的效果变坏。而我们需要网络对所有样本的误差和足够小,因此,往往需要再进行下一轮的训练。直到所有样本的误差达到预期为止。
采用随机梯度下降法,虽然每次训练只使用一个样本,单次迭代的速度很快,但是通过单个样本计算出的梯度不能够很好的体现全体样本的梯度。各个样本各自为政,横冲直撞,不同样本的训练结果,往往会互相抵消,导致参数更新非常的频繁,因此,可能会走很多的弯路,在最优点附近晃来晃去,却无法快速收敛,即使损失函数是凸函数,也无法做到线性收敛,而且采用这种方法,每次只使用一个样本,也不利于实现并行计算。
实际上这种方法很少使用,现在我们所说的随机梯度下降通常是指小批量梯度下降算法。
小批量梯度下降法
小批量梯度下降算法是前面两种的折中方案,也称为小批量随机梯度下降算法。
这种算法把梯度称为若干个小批量,也叫做小批量。也就是每次迭代只使用其中一个小批量来训练模型。下图为小批量梯度下降法的损失函数的计算公式:
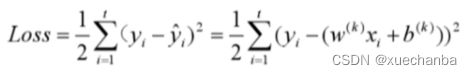
其中, t 是每一批中样本的数量,通常为 1 到几百。
下图为小批量梯度下降法的参数更新迭代公式,
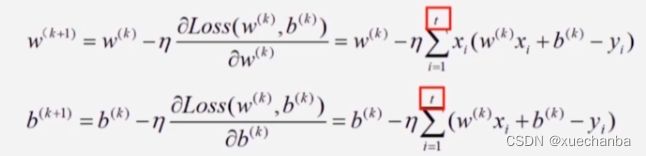
在小批量梯度下降法中,每个批中的所有样本共同决定了本次迭代中梯度的方向,这样训练起来就不会跑偏,也就减少了随机性。
将所有的批次都执行一遍,就称之为一轮。
因为各个批的样本之间也会存在训练结果互相抵消的问题,因此通常也需要经过多轮训练才能够收敛。
使用这种方法的好处是,无论整个训练集的样本数量有多少,每次迭代所使用的训练样本数量都是固定的。
例如,某个训练集中有 2000 个样本,分成 10 批,每个批次中的样本数量是200,那么每次训练就使用1个批中的 200 个样本,每一轮需要进行 10 次训练,如果训练样本增加到 200000 个,分成 1000 批,每个批次中的样本数量是200,那么每次训练同样也是使用1个批中的 200 个样本。
和批量梯度下降法相比,这样显然可以大大的加快训练速度,另外,和批量梯度下降法一样,这种方法也可以实现并行计算。因此。在训练大规模数据集时,通常首选小批量梯度下降算法。
抽样
小批量梯度下降算法是基于统计学中抽样的思想,无论训练样本是数字、图片还是语音,我们从中随机抽取出来一部分样本,它们的特征可以在一定程度上代表整个完整数据集的特征。就像归纳总结人的特征,其实并不需要将世界上所有的人都进行一遍调查,只需要抽取有代表性的一部分样本,覆盖所有的人种、年龄、性别等特征,再对它们进行归纳就可以了。
因此从理论上来说,每次所构建的小批量样本都应该是独立同分布的,能够代表整个样本集的特征。但是,在实际实现时,是很难做到这一点的,每次随机抽取的小批量样本的特征和整体样本的特征存在差别。
例如,有 1000 个小球,分别标记1 — 1000 的数字,
拿出其中所有的小球计算它们的平均值,那就是 500.5,但是从中随机抽取 100 个小球去计算平均值,那么就会出现偏差,结果不会正好是 500.5 ,
同样采用小批量样本计算出的梯度和使用全体样本计算出的标准梯度之间存在偏差,因此,不能保证每次迭代都是向着损失值下降最快的方向前进,也可能会绕远,但是总体来说,还是会向着最优的方向前进。另一方面,小批量中这种梯度偏差就好像是给样本中增加了噪声,会在一定程度上提高模型的泛化能力。
假设下图为某种二元损失函数及其对应的曲面图,
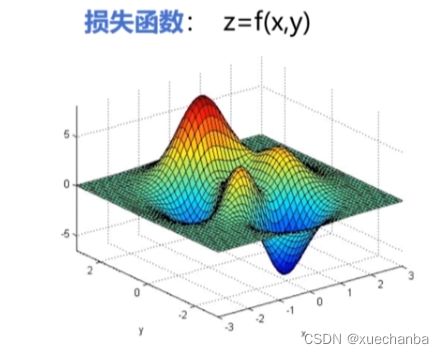
这个曲面中不同的颜色对应不同的函数值,也就是 z 轴坐标。
梯度下降法就是从某个随机点出发,逐步到达全局最小值点,或者某个局部极小值点。
在 xoy 平面上,做出这个函数的等高线,
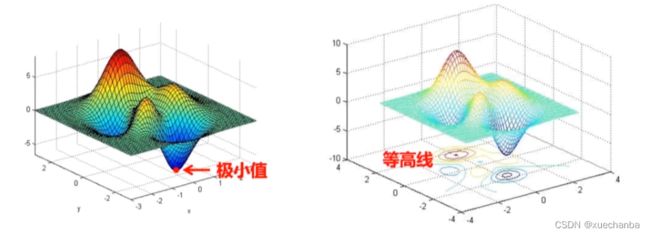
其中,每一个圆圈或者曲线上的高度值都相同。
下面就来借助于等高线来更加直观的看一下这几种梯度下降法的迭代过程。
假设这个函数的损失函数是一个凸函数,这些蓝色的封闭曲线是等高线,下图红色的点为全局最小值点,

在使用批量梯度下降法时,参数更新,每一步都沿着梯度方向向着最小值点前进,迭代次数最少。但是每次迭代所花费的时间非常长,

在使用随机梯度下降法时,虽然每次迭代速度很快,但是它们并不都是向着最小值点的方向前进的,会出现剧烈的振荡。算法会在这种振荡中逐渐走向最小值的位置。
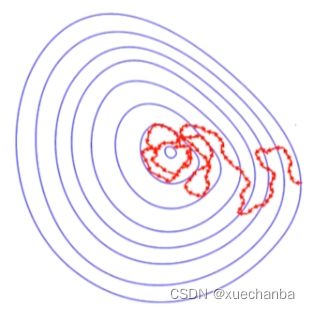
但是也可能会在最小值的周围左右徘徊,始终无法到达。
而使用小批量梯度下降算法,虽然也不是每一次都向着最小值点的方向前进,但是也不会绕着太远。所需要的迭代次数也远远小于随机梯度下降法。