LeetCode 322 周赛
2490. 回环句
句子 是由单个空格分隔的一组单词,且不含前导或尾随空格。
- 例如,
"Hello World"、"HELLO"、"hello world hello world"都是符合要求的句子。
单词 仅 由大写和小写英文字母组成。且大写和小写字母会视作不同字符。
如果句子满足下述全部条件,则认为它是一个 回环句 :
- 单词的最后一个字符和下一个单词的第一个字符相等。
- 最后一个单词的最后一个字符和第一个单词的第一个字符相等。
例如,"leetcode exercises sound delightful"、"eetcode"、"leetcode eats soul" 都是回环句。然而,"Leetcode is cool"、"happy Leetcode"、"Leetcode" 和 "I like Leetcode" 都 不 是回环句。
给你一个字符串 sentence ,请你判断它是不是一个回环句。如果是,返回 true ;否则,返回 false 。
提示
1 <= sentence.length <= 500sentence仅由大小写英文字母和空格组成sentence中的单词由单个空格进行分隔- 不含任何前导或尾随空格
示例
输入:sentence = "leetcode exercises sound delightful"
输出:true
解释:句子中的单词是 ["leetcode", "exercises", "sound", "delightful"] 。
- leetcode 的最后一个字符和 exercises 的第一个字符相等。
- exercises 的最后一个字符和 sound 的第一个字符相等。
- sound 的最后一个字符和 delightful 的第一个字符相等。
- delightful 的最后一个字符和 leetcode 的第一个字符相等。
这个句子是回环句。
思路
模拟,由于只由单个空格分开,则定位到每个空格的位置,比较空格前后两个字符是否相同即可。
class Solution {
public:
bool isCircularSentence(string s) {
int n = s.size();
if (s[0] != s[n - 1]) return false;
int i = 0;
while (i < n) {
while (i < n && s[i] != ' ') i++;
if (i + 1 < n && s[i - 1] != s[i + 1]) return false;
i++;
}
return true;
}
};
2491. 划分技能点相等的团队
给你一个正整数数组 skill ,数组长度为 偶数 n ,其中 skill[i] 表示第 i 个玩家的技能点。将所有玩家分成 n / 2 个 2 人团队,使每一个团队的技能点之和 相等 。
团队的 化学反应 等于团队中玩家的技能点 乘积 。
返回所有团队的 化学反应 之和,如果无法使每个团队的技能点之和相等,则返回 -1 。
提示
2 <= skill.length <= 10^5skill.length是偶数1 <= skill[i] <= 1000
示例
输入:skill = [3,2,5,1,3,4]
输出:22
解释:
将玩家分成 3 个团队 (1, 5), (2, 4), (3, 3) ,每个团队的技能点之和都是 6 。
所有团队的化学反应之和是 1 * 5 + 2 * 4 + 3 * 3 = 5 + 8 + 9 = 22 。
思路
今天(2022/12/21)重做时的思路是,要想每2个人的和相同,如果有可能达到,则将数组从小到大排序后,第一小和第一大的配对,第二小和第二大的配对,…,这样一定是一种合法的方案。
要证明这个结论也比较简单,采用反证法即可,设最小的数为min,最大的数为max,如果min不是和max匹配,那么min一定是和另一个小于max的数匹配,这一组的和一定是小于min + max的;并且,max一定是和另一个大于min的数匹配,这一组的和一定是大于min + max的,这样,至少这两组的和就一定不是相等的。于是便能推导出,如果存在合法方案,则min一定是和max匹配。然后我们可以将min和max从数组中移出去,再看数组剩余部分的新的最大值和最小值,同样用上面的反证思路可以推出,原数组中第二小的数,一定是和第二大的数匹配,… 这样最终就能推出,一定是要排序后,两端的数进行匹配。
但由于用到了排序,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),并不是很优秀。
class Solution {
public:
long long dividePlayers(vector<int>& skill) {
sort(skill.begin(), skill.end());
long long ans = 0;
int i = 0, j = skill.size() - 1;
int sum = -1;
while (i < j) {
int t = skill[i] + skill[j];
if (sum == -1) sum = t;
else if (sum != t) return -1;
ans += skill[i] * skill[j];
i++;
j--;
}
return ans;
}
};
周赛当天的思路比较朴素,首先,如果存在合法方案,由于共有n / 2个组,而且每个组中2个数字的和要相同,设整个数组的和为sum,则每一组的和固定是2 * sum / n。则对于每个元素skill[i],和其配对的另一个元素一定是2 * sum / n - skill[i],我们只需要统计每个数出现的次数,以及某个数被另一个数所匹配的次数即可,然后遍历一次数组,判断每个元素是否能被匹配即可。
用到了哈希表,总的时间复杂度为 O ( n ) O(n) O(n)
typedef long long LL;
const int N = 1010;
class Solution {
public:
int cnt[N]; // 某个数的出现次数
int used[N]; // 某个数被别的数匹配的次数
LL dividePlayers(vector<int>& skill) {
int n = skill.size();
int tot = 0;
for (int i = 0; i < n; i++) {
tot += skill[i];
cnt[skill[i]]++;
}
int sum = tot * 2 / n; // 每个团队应该分配的
if (sum * n / 2 != tot) return -1; // 和不为整数, 直接退出
bool flag = true;
LL ans = 0;
for (int i = 0; i < n; i++) {
int x = skill[i];
if (used[x] > 0) {
used[x]--;
continue; // 该数被其他数匹配过, 则使用的次数-1, 并跳过该数
}
// 该数没有被其他数匹配过, 则尝试给该数寻找匹配, 首先减掉该数
cnt[x]--; // 该数出现次数减1
if (sum - x >= 0 && cnt[sum - x] > 0) {
// 与之互补的数如果存在, 且剩余可用次数大于0
ans += (sum - x) * x;
cnt[sum - x]--; // 这个数使用次数减1
used[sum - x]++; // 这个数被其他数匹配过一次
} else {
// 如果无法匹配, 则退出
flag = false;
break;
}
}
if (flag) return ans;
return -1;
}
};
2492. 两个城市间路径的最小分数
给你一个正整数 n ,表示总共有 n 个城市,城市从 1 到 n 编号。给你一个二维数组 roads ,其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条 双向 道路,道路距离为 distancei 。城市构成的图不一定是连通的。
两个城市之间一条路径的 分数 定义为这条路径中道路的 最小 距离。
城市 1 和城市 n 之间的所有路径的 最小 分数。
注意:
- 一条路径指的是两个城市之间的道路序列。
- 一条路径可以 多次 包含同一条道路,你也可以沿着路径多次到达城市
1和城市n。 - 测试数据保证城市
1和城市n之间 至少 有一条路径。
提示:
2 <= n <= 10^51 <= roads.length <= 10^5roads[i].length == 31 <= ai, bi <= nai != bi1 <= distancei <= 104- 不会有重复的边。
- 城市
1和城市n之间至少有一条路径。
示例
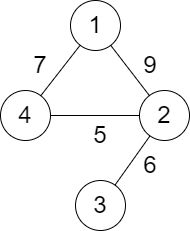
输入:n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出:5
解释:城市 1 到城市 4 的路径中,分数最小的一条为:1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。
思路
假设两个城市中间存在路径,这也就是说两个城市是互相连通的,或者 两个城市处于同一个连通块,而两个城市之间的一条路径的分数,定义为这条路径中最短的那条边,且一条路径可以多次包含一条边。那么,只要2个城市位于同一个连通块中,则这两个城市之间的所有路径的最小分数,一定是这个连通块中权重最小的那条边。
由于关键的性质在于判断2个城市是否连通,所以很自然的想到了并查集。我们只要遍历全部的边,依次合并节点即可,并在合并的过程中,实时维护某一连通块中最小权重的边即可。
这道题目是个简单的并查集。
class Solution {
public:
int find(int x, vector<int>& p) {
if (x != p[x]) p[x] = find(p[x], p);
return p[x];
}
int minScore(int n, vector<vector<int>>& roads) {
vector<int> p(n + 1);
vector<int> score(n + 1, 1e4);
for (int i = 1; i <= n; i++) p[i] = i;
for (auto& r : roads) {
int a = r[0], b = r[1], c = r[2];
int pa = find(a, p), pb = find(b, p);
if (pa != pb) {
p[pa] = pb;
score[pb] = min(score[pb], score[pa]);
}
// 如果已经位于同一连通块, 由于纳入了一条新的边, 则也要更新score
score[pb] = min(score[pb], c);
}
return score[find(n, p)];
}
};
当然,也可以使用图的遍历(DFS或BFS)来做
const int N = 1e5 + 10, M = 2* N;
class Solution {
public:
int h[N], e[M], w[M], ne[M], idx;
bool st[N];
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
int ans = 1e4;
// 由于1到n一定存在至少一条路径, 只需要深搜1所在的连通块, 走过所有的边,并更新答案即可
void dfs(int x) {
st[x] = true;
for (int i = h[x]; i != -1; i = ne[i]) {
int u = e[i], v = w[i];
ans = min(ans, v); // 更新答案要放在下面的if之前, 因为有的边可能会指向已经走过的点, 但这条边还未被走过
if (st[u]) continue;
dfs(u);
}
}
int minScore(int n, vector<vector<int>>& roads) {
memset(h, -1, sizeof h);
for (auto& r : roads) {
int a = r[0], b = r[1], c = r[2];
add(a, b, c);
add(b, a, c);
}
dfs(1);
return ans;
}
};
2493. 将节点分成尽可能多的组
给你一个正整数 n ,表示一个 无向 图中的节点数目,节点编号从 1 到 n 。
同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 双向 边。注意给定的图可能是不连通的。
请你将图划分为 m 个组(编号从 1 开始),满足以下要求:
- 图中每个节点都只属于一个组。
- 图中每条边连接的两个点
[ai, bi],如果ai属于编号为x的组,bi属于编号为y的组,那么|y - x| = 1。
请你返回最多可以将节点分为多少个组(也就是最大的 m )。如果没办法在给定条件下分组,请你返回 -1 。
提示:
1 <= n <= 5001 <= edges.length <= 10^4edges[i].length == 21 <= ai, bi <= nai != bi- 两个点之间至多只有一条边。
示例
输入:n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
输出:4
解释:如上图所示,
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组,将第三个组或者第四个组中任何一个节点放到第五个组,至少有一条边连接的两个节点所属的组编号不符合题目要求。
思路
分层图,网络流。
起点固定后,层数最大值就是BFS求得的最短路径树的高度。
直观思路
我们先选定一个初始点start,从这个点开始进行扩展并分组,设start所在的分组为第一组,那么所有start的邻接点都一定位于第二组;而对于第二组中所有的点,其邻接点,由于只需要保持距离的绝对值为1,则其邻接点可以位于第一组,也可以位于第三组。从直觉的角度来讲,要组数最多,那么分组时要尽可能的往外延伸,而不应该走回头路。那么当初始点start固定后,我们不断的遍历每一组的所有邻接点,往外延伸,就能得到当初始点固定为start时,最多的分组的情况。由于是沿着每一组的邻接点,一圈一圈的往外进行扩展,这个过程和BFS非常像,所以我们可以用BFS来模拟这个过程。
但上面讨论的是初始点固定的情况下,实际我们可以选择不同的点作为初始点,进行扩展,得到的结果可能不一样。周赛当天我就是陷入了这种思维,企图通过某种贪心的策略(比如邻接点的个数),来找到一个最佳的初始点,使得以这个点作为初始点进行扩展时,能延伸的尽可能的远。
实际可以直接暴力枚举,枚举每个点作为初始点,最远能扩展到多远,然后取一个最大值即可。
另外有几个点需要注意:
-
整个图可能是不连通的
这也就意味着可能存在着多个连通块,对于多个连通块的情况,若像整个图的分组数尽可能大,那么不同连通块中的分组不应该有交集。所以我们可以单独对每个连通块进行处理,求出每个连通块内部的最大分组数,然后将所有连通块的最大分组数进行相加,就能得到整个图的最大分组数
-
选定初始点后,为何第一组中只有初始点这一个点
需要稍微证明下,为什么把初始点单独放在第一组里,是正确的。
也是采用反证的思路,若除初始点以外,把其他的某些点,也放在第一组内,则这些点一定不是初始点的邻接点,如果把这些点放在后面的组,而不放在第一组,则这些点的邻接点能够往外扩展的更远。因为如果把这些点放在第一组,则这些点的邻接点延伸出来的距离,有一部分是会和初始点延伸出来的距离重合(对最远的距离的贡献有所重合)。所以单独把初始点放在第一组,一定不会比放多个点在第一组更差
-
什么时候无法分组?
我们对某一个连通块求解最大分组时,是通过BFS一圈一圈往外扩展的,我们知道每个组之间的距离为1。其实在BFS过程中,每一组可以看成是BFS的每一层,而最大分组数就是BFS的最大层数。
什么时候无法分组呢,就是出现了矛盾的时候。即,当BFS中的某一层中的两个点之间存在边,则矛盾。这个结论可以自行验证。(其实也等价于用染色法来判定二分图,因为当某一层的两个点之间存在边,首先我们可以找到这两个点的最近公共祖先,这两个点到其最近公共祖先的路径长度是相等的,设为
x,由于这两个点之间存在边,那么这两个点和其最近公共祖先,会形成一个环,环的长度为2x + 1,是个奇数环)只要在某个连通块中,以某个特定的点作为初始点,进行BFS过程中出现了同一层的两个点之间存在边,那么这个连通块就无法分组了,就算换其他的点作为初始点也一样。因为上面推导出了,此时这个连通块中是存在奇数环的,则无论以哪个点作为BFS的起始点,这个奇数环仍然是存在的,则在BFS过程中一定还会出现某一层的两个点之间存在边的情况。
所以只要某一次BFS过程中出现了这种情况,就可以直接
return -1了
那么思路就比较清楚了。我们先将整个图分成若干个连通块(若整个图不连通),然后对每个连通块,以这个连通块中所有的点作为初始点,分别做一次BFS,求出最大层数,然后再取一个最大值,就求得了这个连通块的最大分组数,最后将全部连通块的最大分组数相加,就是最终答案。
那么思路就是
- 并查集 + BFS
也可以两次遍历
- DFS + BFS 或 两次BFS 之类
y总讲解
再贴一下y总的部分讲解
首先,对于图中的某两个点之间形成的一条路径,假设这条路径的长度为n(包含n + 1个点),那么这条路径上的所有点,最多能被分成n + 1组,因为需要分最多的组,我们沿着这条路径走过每个点时,都尽可能往同一个方向进行扩展。举个例子比如单链表形状的1 - 2 - 3 - 4,最多能分成4组,而最少,就是每次往回折返,分成2组。
对于某两个点a和b,它们之间可能存在多条路径,假设它们之间存在m条路径。我们对每条路径i ∈ [0, m - 1],设这条路径的长度为L[i]。设整个图的最大分组数为g,则从a和b上的每条路径来看,
一定有 L[i] + 1 >= g
因为单从某条路径i来看,以这条路径为准,最多能划分的分组为L[i] + 1,这是根据这条路径,能划分出的最大的分组数,那么理应大于等于整个图的最大分组数。
于是有
L[0] + 1 >= g
L[1] + 1 >= g
...
L[m - 1] + 1 >= g
对于a和b之间的所有m条路径,上面的不等式都要同时成立。
设a和b之间最短的路径为k,那么一定有L[k] + 1 >= g,即整个图的最大分组数,一定是受限制于a和b之间的最短的那条路径。
这里描述有点不太准确,准确的说,不是整个图,而是对于a到b的最短路径上的所有点来说。如果有点在a到 b的路径以外,那么分组数还可以继续扩大。
由于是求解最短路,那么我们只需要固定一个起点,然后用BFS生成一颗最短路径树,这棵树上初始点到最远处的点之间的路径,就是这个连通块的最大分组数。
其余部分和上面的思路一样,不再赘述。
正解代码
并查集+BFS:
class Solution {
public:
vector<vector<int>> g;
vector<int> p;
vector<int> pDis; // 每个并查集的最长分组数
vector<bool> st;
vector<int> dis; // 距离
int INF = 1e4 + 10; // 距离无穷大
int n;
// 并查集模板
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
bool bfs(int start) {
// 初始化距离
for (int i = 1; i <= n; i++) dis[i] = INF;
queue<int> q;
q.push(start);
dis[start] = 0;
int clock = 0; // 记录当前的层数
while (!q.empty()) {
clock++;
int size = q.size();
for (int i = 0; i < size; i++) {
int x = q.front();
q.pop();
for (int& u : g[x]) {
if (dis[u] == clock - 1) return false;
if (dis[u] > clock) {
// dis[u] = clock 的不要再放入队列里了会超时
dis[u] = clock;
q.push(u);
}
}
}
}
int ps = find(start); // 找到这个起点对应的连通块
pDis[ps] = max(pDis[ps], clock); // 用当次起点BFS时的最大层数, 去更新所属连通块的最大分组数
return true;
}
int magnificentSets(int n, vector<vector<int>>& edges) {
g.resize(n + 1);
p.resize(n + 1);
pDis.resize(n + 1);
st.resize(n + 1);
dis.resize(n + 1);
this->n = n;
// 并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
// 建图
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
// a和b有一条边, 进行合并
p[find(a)] = find(b);
}
// 对所有点进行BFS
for (int i = 1; i <= n; i++) {
if (!bfs(i)) return -1;
}
int ans = 0;
for (int i = 1; i <= n; i++) {
int pi = find(i); // 查找这个点所在的连通块
if (st[pi]) continue;
st[pi] = true; // 这个连通块被访问过了
ans += pDis[pi]; // 累加答案
}
return ans;
}
};
还可以用DFS+BFS
class Solution {
public:
vector<vector<int>> g;
vector<int> v;
vector<bool> st;
vector<int> color;
vector<int> dis;
int n;
int INF = 1e4 + 10;
bool dfs(int x, int c) {
color[x] = c;
v.push_back(x);
for (auto& u : g[x]) {
if (color[u] == color[x]) return false;
if (color[u] == 0 && !dfs(u, 3 - c)) return false;
}
return true;
}
int bfs(int x) {
for (int i = 1; i <= n; i++) dis[i] = INF;
int clock = 0;
queue<int> q;
q.push(x);
dis[x] = 0;
while (!q.empty()) {
clock++;
int size = q.size();
for (int i = 0; i < size; i++) {
int u = q.front();
q.pop();
for (auto& o : g[u]) {
if (dis[o] == clock - 1) return false; // 同一层2个点之间有边
if (dis[o] > clock) {
// dis[o] = clock 时不要加入队列了, 无效的重复计算会超时
dis[o] = clock;
q.push(o);
}
}
}
}
return clock;
}
int magnificentSets(int n, vector<vector<int>>& edges) {
this->n = n;
g.resize(n + 1);
st.resize(n + 1);
color.resize(n + 1);
dis.resize(n + 1);
// 建图
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
int ans = 0;
// 用dfs来将同一连通块中的点都加入到v
for (int i = 1; i <= n; i++) {
if (color[i]) continue; // 这个点访问过了已经, 已经被染过色了
v.clear(); // 清空容器, 准备接收该连通块的所有点
if (!dfs(i, 1)) return -1; // 先深搜该连通块, 添加点并染色, 若染色失败, 直接return
int mx = 0;
for (auto& u : v) mx = max(mx, bfs(u)); // 将该连通块中所有点依次作为初始点, 进行BFS, 并取最大值
ans += mx;
}
return ans;
}
};
错误回顾
今天(2022/12/21)看完题解后,我自己的一种做法是,先分组,将同一连通块的所有点放在一起,然后依次处理每个连通块。
但是一直超时,是因为把大量无效的点加入了队列,导致了很多无效的重复计算。
其实上面正解的部分,直接对全部的点作为起点进行BFS,然后再分组判断就好了。代码上更加简洁。
class Solution {
public:
vector<int> p;
vector<vector<int>> g;
vector<int> dis;
unordered_map<int, vector<int>> group; // 每个连通块中的全部节点
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int bfs(vector<int>& v, int n) {
// printf("新的连通块\n");
int ans = 0;
for (auto& i : v) {
for (int j = 1; j <= n; j++) dis[j] = n;
queue<int> q;
q.push(i);
dis[i] = 0;
int mx = 0;
while (!q.empty()) {
int ss = q.size();
for (int j = 0; j < ss; j++) {
int x = q.front();
q.pop();
for (auto& u : g[x]) {
if (dis[u] == dis[x]) return -1; // 同一层
if (dis[u] < dis[x]) continue;
// 这里不对, 若dis[u] == dis[x] + 1 的话, 其实是不需要再放到队列中了
// 自己调试了下, 此时再放到队列中, 会增加很多无效的计算, 时间消耗会多一个数量级, 自然就超时了
dis[u] = dis[x] + 1;
mx = max(mx, dis[u]);
q.push(u);
// 应当改成
/**
if (dis[u] > dis[x] + 1) {
dis[u] = dis[x] + 1;
mx = max(mx, dis[u]);
q.push(u);
}
**/
}
}
}
// printf("以%d为起点, 最长的路径长度为%d\n", i, mx);
ans = max(ans, mx + 1);
}
return ans;
}
int magnificentSets(int n, vector<vector<int>>& edges) {
p.resize(n + 1);
g.resize(n + 1);
dis.resize(n + 1);
for (int i = 1; i <= n; i++) p[i] = i;
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
p[find(a)] = find(b); // 合并
}
// 分组
for (int i = 1; i <= n; i++) {
group[find(i)].push_back(i);
}
int ans = 0;
for (auto&[k, v] : group) {
int x = bfs(v, n); // 对这个连通块里的全部的点, 依次作为起点做一次bfs
if (x == -1) return -1; // 该连通块无法正确分组
ans += x;
}
return ans;
}
};
回看了下周赛当天的代码,也想到了连通块和BFS,但是当时没有枚举所有点做BFS,而是固定以连通块中,边数最少的点作为起点。只通过了46/55个样例。
const int N = 510, M = 2e4 + 10;
class Solution {
public:
bool edgeSt[N][N];
int p[N], val[N]; // 并查集, 连通块中边最少的节点
int h[N], e[M], ne[M], idx;
int cntE[N]; // 与这个点相连的有多少条边
bool st[N]; // 是否在队列中
int group[N]; // 所属组
int ans = 0; // 组数
bool flag = true;
// 从root开始进行bfs
void bfs(int root) {
// printf("开始BFS, root = %d\n", root);
queue<int> q;
q.push(root);
st[root] = true;
while (q.size()) {
queue<int> tmp;
int ss = q.size();
ans++; // 组数+1
for (int i = 0; i < ss; i++) {
int x = q.front(); // 访问这个点
q.pop();
group[x] = ans; // 这个节点所属的组
// printf("x = %d所属的组为%d\n", x, ans);
// 访问全部相邻节点
for (int i = h[x]; i != -1; i = ne[i]) {
// printf("访问x=%d的邻接点u=%d\n", x, e[i]);
int u = e[i];
if (edgeSt[x][u]) {
// printf("x=%d,u=%d, 这条边已经走过\n", x, u);
continue; // 这条边已经走过, 不往回走
}
if (st[u]) {
// printf("u=%d,已在队列中\n", u);
flag = false;
break;
}
// 若这个相邻点已有所属组
if (group[u]) {
// printf("u=%d,已经有所属组为%d\n", u, group[u]);
// 且两者相差不为1, 则提前返回
if (abs(group[u] - group[x]) != 1) {
// printf("相邻点u=%d, 已有所属组%d, 且二者相差不为1\n", u, group[u]);
flag = false;
return ;
}
edgeSt[x][u] = edgeSt[u][x] = true;
} else if(!st[u]) {
// 没有所属组, 且不在队列中
// printf("u=%d,没有所属组\n", u);
edgeSt[x][u] = edgeSt[u][x] = true;
// 这个相邻点没有所属组, 则加入到下一轮的bfs
tmp.push(u);
}
}
}
while (tmp.size()) {
int x = tmp.front();
tmp.pop();
q.push(x);
st[x] = true;
}
}
}
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
// 选择相连的边数最少的点作为根节点开始进行BFS访问
int magnificentSets(int n, vector<vector<int>>& edges) {
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i++) {
p[i] = i;
val[i] = i;
}
for (auto& e : edges) {
int a = e[0], b = e[1];
add(a, b);
add(b, a);
cntE[a]++;
cntE[b]++;
p[find(a)] = find(b); // 并查集合并
}
// 更新连通块中边最少的节点
for (int i = 1; i <= n; i++) {
int pi = find(i);
if (cntE[val[pi]] > cntE[i]) val[pi] = i;
}
for (int i = 1; i <= n; i++) {
if (group[i]) continue; // 这个点已经分过组
// 没有访问过, 则找到这个点所属连通块中边数最小的点开始BFS
int root = val[find(i)];
//printf("root is %d\n", root);
bfs(root);
if (!flag) break;
}
return flag ? ans : -1;
}
};
这样的贪心策略是错误的。比如下面这组数据,边数最小的点位于中间。
13
[[1,4],[1,5],[1,6],[2,4],[2,5],[2,6],[3,4],[3,5],[3,6],[6,7],[7,11],[8,11],[8,12],[8,13],[9,11],[9,12],[9,13],[10,11],[10,12],[10,13]]
画出的图如下
用正解的程序,输出一下以每个点作为BFS的起点,得到的路径长度,如下
起点为1, 最长路径为6
起点为2, 最长路径为6
起点为3, 最长路径为6
起点为4, 最长路径为7
起点为5, 最长路径为7
起点为6, 最长路径为5
起点为7, 最长路径为4
起点为8, 最长路径为6
起点为9, 最长路径为6
起点为10, 最长路径为6
起点为11, 最长路径为5
起点为12, 最长路径为7
起点为13, 最长路径为7
很明显,以边数最短的点7,作为起点,得到的路径长度只有4,是不正确的。
所以这种贪心策略有问题。
总结
T1是简单模拟;T2是哈希表,也可以找规律;T3是个简单的并查集;T4是并查集+BFS求最短路径树的最深层次。
没想到T4可以直接暴力枚举所有点作为BFS的起点,我一开始可高估了时间复杂度,就在往贪心的方向上想,而没想到暴力可以做。