小波分析中图像压缩

charpter 1 小波分析中图像压缩

---

前言

一维的处理通常属于线性型，但生活在三维空间中，最为主要的还是对于二维平面的处理，最为常见的便是对于图像的处理，小波分析就是对于图像信号的处理，小波就是指小的波形，小波就是衰减的波形，不同于我们常见的Fourier变换对波的分析，小波变换更加适用于时间频率的局部分析，对信号的高频或者低频部分进行细化分析，本章主要集中于小波对于图像的处理分析。

一、图像压缩以及实现

图像压缩是对图像最为基本的处理，能够处理的原因：
1.原始图像存在图像冗余，图像冗余包括
空间冗余：景物采样点间存在着空间相关性，相邻各点间取值相近或相同
视觉冗余：视觉系统并不能感知画面的变化部分
结构冗余：图像的架构发生了冗余
2.人眼视觉对于边缘急剧变化敏感，但是人眼对亮度信息敏感对颜色分辨率弱，解压缩后图像依然有满意的的主观质量。

传统的图像处理一般采用K-L变换，即已矢量信号X的协方差矩阵φ的归一化正交特征矢量q所构成的正交矩阵Q，来对该矢量信号X做正交变换Y=QX。（Karhunen-Loeve Transform）

小波压缩的特点：压缩比高，速度快，抗干扰，压缩过程图像特征不会改变。
在小波压缩中考虑到关键因素：核心就是正则性（图像越光滑，其正则性也就越好）,其次还可以考虑到小波基的线性相位，能量集中性等。

接下来的小波压缩方法就是去掉图像的高频部分但是保留最为基本的低频部分用来表征图像的主要部分。
wcodemat函数的调用：
Y=wcodemat(X,NBCODES,OPT,ABSOL)：ABSOL=0，返回输入矩阵X的编码，否则返回abs（X）即绝对值。NBCODES为编码最大值，OPT决定编码的方式：r行编码，c列编码，m矩阵编码。

二、MATLAB实现

1.引入库

First code

 clear all;
load woman;%加载图像
subplot(1,3,1);image(X);%画图1行3列，命名为X
colormap(map);%设置当前颜色
title ('原始图像')
NBCOL = size(map,1);%colormap的范围

[cA1,cH1,cV1,cD1] = dwt2(X,'db1');% 利用db1对图像进行单层二维离散分解
%二维离散小波变换 [cA,cH,cV,cD]=dwt2(X,'wname')用指定小波基函数对二维信号X进行小波变换
%cA,cH,cV,cD分别表示近似分量，水平细节分量，垂直细节分量，对角细节分量
subplot(1,3,2);image(cA1);
colormap(map);
title ('未缩放的图像');
% 对图像进行缩放
cD=wcodemat(cA1,NBCOL);
subplot(1,3,3);image(cD);
colormap(map);
title('缩放图像');

Second Code

clear all;  %清空工作空间变量
load detfingr; %导入图像数据
nbc=size(map,1);%size函数提取图像中的矩阵
[C,S]=wavedec2(X,2,'db4');%图像小波二层分解
thr_h=[21 46];            %设置水平分量阈值
thr_d=[21 46];            %设置对角分量阈值
thr_v=[21 46];            %设置垂直分量阈值   
thr=[thr_h;thr_d;thr_v]; 
[Xcompress2,cxd,lxd,perf0,perfl2]=wdencmp('lvd',X,'db3',2,thr,'h');%进行分层压缩
%[XC,CXC,LXC,PERF0,PERFL2]=wdencmp('gbl',X,'wname',N,THR,SORH,KEEPAPP)
%[XC,CXC,LXC,PERF0,PERFL2]=wdencmp('lvd',X,'wname',N,THR,SORH)
%[XC,CXC,LXC,PERF0,PERFL2]=wdencmp('lvd',C,L,'wname',N,THR,SORH)
%主要用于一维和二维消噪和压缩，wname是所用的小波基函数，gbl全局量每一层采用同一个阈值处理，lvd表示每层用不同的阈值处理
%THR也为一个阈值向量，N为小波分解层次，SOHR表示软阈值或者硬阈值。
%XC是压缩后的信号，CXC,LXC为小波分解结构，PERF0,PERFL2为恢复和压缩的百分比
set(0,'defaultFigurePosition',[100,100,1000,500]);%修改图形图像位置的默认设置
set(0,'defaultFigureColor',[1 1 1])       %修改图形背景颜色的设置
Y=wcodemat(X,nbc);
Y1=wcodemat(Xcompress2,nbc);
figure %显示原图像和压缩图像
colormap(map)
subplot(2,2,1),image(Y),axis square
title('映射数组压缩前图像');
subplot(2,2,2),image(Y1),axis square
title('映射数组压缩后图像');
subplot(2,2,3),image(Y),axis square
title('彩色方式下压缩前原图像');
subplot(2,2,4),image(Y1),axis square
title('彩色方式下压缩后图像');
disp('小波系数中置0的系数个数百分比：')  %显示压缩能量
perfl2
disp('压缩后图像剩余能量百分比：')
perf0

2.结果显示

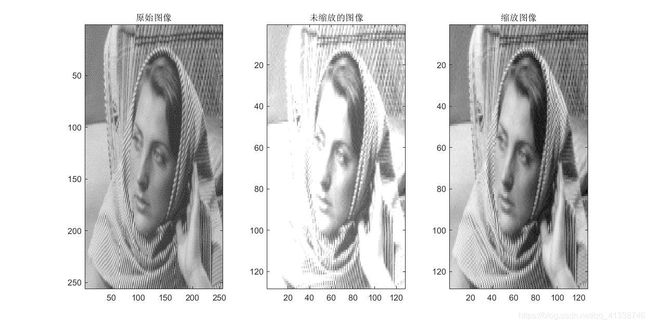压缩后的图像并没有失真，主要特征依然存在，但是颜色更深并且图像数据量更小。
从图像表面看来，图像并没有多大的改变说明图像在压缩过程中并没有改变图像的特征结构，但是根据压缩后的能量比可以清晰的看到数据减少了，说明减少了冗余，完成了数据压缩。

总结

第一部分的总结主要就是对于小波变换的一个了解，以及对于二维图像的处理是学习的重点，图像压缩是最为基本的一种处理方法，dwt2的二维分解，wcodemat函数的量化编码，以及wdencmp的阈值压缩函数是图像压缩的核心！！