Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting 论文笔记

Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting 论文笔记-----GCN在交通领域的应用（二）

一、论文翻译：

1、摘要：

       及时准确地交通预测对于城市交通控制和指导具有至关重要的意义。由于交通流量的非线性和复杂性，传统的方法不能满足中长期预测任务的需求，并且往往会忽略时空数据的时间和空间依赖特性。在这篇论文中，为了处理在交通领域的时间序列预测问题，我们提出一种新颖的深度学习框架，时间空间图卷积网络（STGCN）。不同于引用常规的卷积和循环单元，我们在图上建模预测问题，并且用完整的卷积结构来建模模型。这样的模型有更快的训练速度更少的参数。实验显示我们的模型通过对多尺度交通网络进行建模，有效地捕捉了综合时空关联，并在各种实际交通数据集上始终优于最先进的基线。

2. 定义

2.1 图上的交通预测的定义

交通预测是一个经典的时间序列预测问题。根据先前的M个时间步的交通观测量，预测接下来H个时间步的交通观测量（速度或者流量）。公式如下所示：

在上述公式中，vt∈Rn表示n个路段在时间步t的观测向量，向量中的每个元素表示一个路段在一个时间点的交通观测值。在这篇论文中，在图上定义一个交通网络并且集中于结构化的交通时间序列。观测向量vt不是独立的，而是通过图中的成对连接连接起来的。因此，在下图中，数据点vt是在无向图G上的一个图信号，图的权重表示为wij。在第t个时间步，图Gt=(Vt,E,W)， Vt表示顶点的集合，表示交通网络中n个监测站点在时刻t的监测值，E是边的集合，表示站点之间的连接情况，W表示图G的权重邻接矩阵。

3. 提出的模型

3.1网络结构

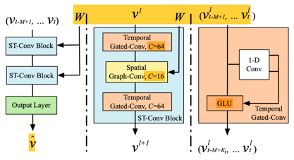
在这一节，我们详细介绍我们提出的模型架构：时间空间图卷积网络（STGCN）。如图所示，

STGCN模型由两个时间空间图卷积模块（ST-Conv block ）和一个全连层（输出层）组成。每个时间空间卷积模块（ST-Conv block ）包含两个时间门控卷积层和一个在中间的空v间图卷积层。并且残差连接和瓶颈策略被应用到了上述的每个模块中。输入Vt-M+1,...,Vt由ST-Conv块统一处理，来探索空间和时间依赖性。 输出层集成了所有的特征，来生成最终预测v

二、模型架构的整体理解（结合代码进行的理解）：

1、输入理解：

对于模型架构，如上图所示，输入的维度是[batch_size, time_step, n_route, c_in]

对于输入的解释：

在本文中，有n个路段，即n_route=n; 观察每个路段的速度值，因此每个站点的特征维度为1，即C_in = 1; 根据先前M个时间步的观测状态预测接下来的时间点的状态，因此time_step = M.

在每个时间点t，对n个站点的速度采样，即维度是n*1；因此对于M个时间点，维度是M*n*1；其中M对应time_step（采样点的数目）,n对应n_route（站点的数量）；1对应c_in（一维速度特征）。

构造好输入之后，下面看网络层的搭建：

2、门控时间卷积：

首先第一部分是门控时间卷积：

门控时间卷积的组成如下：

1、包含一个1D因果卷积和一个GLU门控线性单元 （Gated Linear Units）

2、又叠加了一个残差网络架构

1D因果卷积：处理时间序列问题；即根据先前的M个时间步的值，预测下一个时间步的值，如下图所示：

其中input中每个位置对应一个时间步，时间步内可以是多维的数据。先按一维数据比较容易理解，则图中，卷积核就是一个2*1的卷积核，然后在第一层依次移动，最左边做padding，得到第二层，然后依层传递下去，即得到因果的效果。

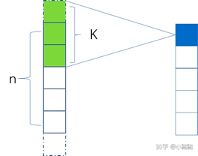
1D卷积的计算过程如下图所示：

其中K表示卷积核

GLU激活函数

GLU的公式如下所示：

表示一个没有非线性函数的卷积层输出点积一个经过sigmod非线性激活函数的卷积层输出，具体结构如下图所示：

GLU激活函数的优点：

（1）进行深度网络建模；

（2）能减轻梯度弥散，加速收敛；

（3）GLU和Relu都拥有线性通道，可以使梯度很容易通过激活的units，反向传播且不会减小。因此，采用GLU或Relu做为激活，训练时收敛速度更快。

上述过程对应论文中的公式如下所示：

其中P和Q表示因果卷积的输出拆成的两部分（P表示前C通道，Q表示后C通道）。上述公式是GLU激活函数公式的套用。

残差架构：

随着网络层数的增加，网络发生了退化（degradation）的现象：随着网络层数的增多，训练集loss逐渐下降，然后趋于饱和，当你再增加网络深度的话，训练集loss反而会增大。

门控时间卷积架构的优势：

（1）、是一种卷积语言建模方式，相比RNN等模型易于训练，结构简单，可用于时间序列建模

（2）、容易实现并行化

（3）、减少梯度消失

3、GCN提取空间特征

GCN的公式化表示（奈何数学知识不够，论文中的GCN的推导没有看懂，但是理解了GCN最后推导出的公式）：

在上述公式中，W表示邻接矩阵，

I表示单位矩阵；D表示W的度矩阵，x表示输入；θ表示权重参数；

对上述公式进行简单理解，如下所示：

其中A对应上述的W，H表示输入x，W表示权重参数，σ表示激活函数。

4、模型的输入：

1、n个站点， 一个时刻的观测向量维度是n*1；因此， M个时刻，n个站点的观测向量维度是M*n*1；

输入一：因此输入的向量维度是M*n*1

输入二：表示站点之间的连接关系的邻接矩阵W，维度是n*n。（用于GCN模型的输入）

 

模型的输出：

下一时刻n个站点的状态值，因此是n*1

对应论文的公式化表示：

三、论文整体模型的公式化表示流程：

1、首先进行时间门控卷机提取时间特征：

输入数据通过1D因果卷积（卷积核是kt），变成2C通道的向量，然后经过GLU激活函数，如下所示：

2、然后进行图卷积提取空间特征：

3、最后一个全连接层输出预测目标，损失函数如下所示：