神经网络、结构、权重和矩阵
介绍
我们在机器学习教程的前一章中介绍了有关神经网络的基本思想。
我们已经指出了生物学中神经元和神经网络之间的相似性。我们还引入了非常小的人工神经网络,并引入了决策边界和 XOR 问题。
在我们到目前为止介绍的简单示例中,我们看到权重是神经网络的基本部分。在开始编写具有多层的神经网络之前,我们需要仔细查看权重。
我们必须了解如何初始化权重以及如何有效地将权重与输入值相乘。
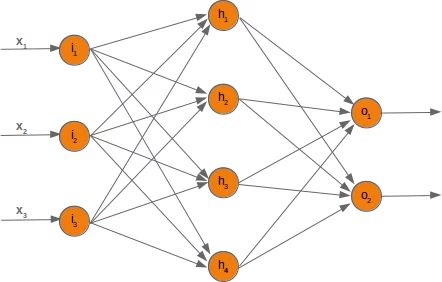
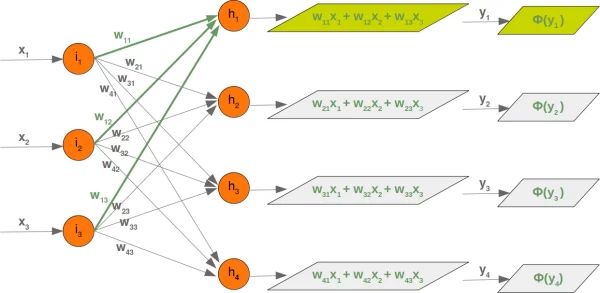
在接下来的章节中,我们将用 Python 设计一个神经网络,它由三层组成,即输入层、隐藏层和输出层。您可以在下图中看到这种神经网络结构。我们有一个包含三个节点的输入层一世1,一世2,一世3 这些节点得到相应的输入值 X1,X2,X3. 中间或隐藏层有四个节点H1,H2,H3,H4. 该层的输入源于输入层。我们将很快讨论该机制。最后,我们的输出层由两个节点组成○1,○2
输入层与其他层不同。输入层的节点是被动的。这意味着输入神经元不会改变数据,即在这种情况下没有使用权重。他们接收一个值并将这个值复制到他们的许多输出中。
输入层由节点组成 一世1, 一世2 和 一世3. 原则上,输入是一维向量,如 (2, 4, 11)。一维向量用 numpy 表示,如下所示:
将 numpy 导入为 np
输入向量 = np 。数组([ 2 , 4 , 11 ])
打印( input_vector )
输出:
[ 2 4 11]
在我们稍后将编写的算法中,我们必须将其转置为列向量,即只有一列的二维数组:
将 numpy 导入为 np
输入向量 = np 。数组([ 2 , 4 , 11 ])
input_vector = np 。数组(input_vector , ndmin = 2 )。T
打印(“输入向量:\n ” , input_vector )
打印(“这个向量的形状:” , 输入向量。形状)
输出:
输入向量:
[[2]
[4]
[11]]
这个向量的形状:(3, 1)
权重和矩阵
我们网络图中的每个箭头都有一个相关的权重值。我们现在只看输入层和输出层之间的箭头。
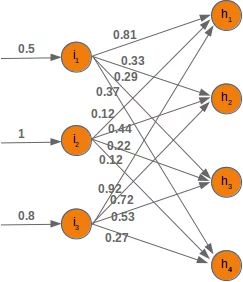
价值 X1 进入节点 一世1将根据权重的值进行分配。在下图中,我们添加了一些示例值。使用这些值,输入值 (一世H1,一世H2,一世H3,一世H4 进入节点(H1,H2,H3,H4) 的隐藏层可以这样计算:
一世H1=0.81*0.5+0.12*1+0.92*0.8
一世H2=0.33*0.5+0.44*1+0.72*0.8
一世H3=0.29*0.5+0.22*1+0.53*0.8
一世H4=0.37*0.5+0.12*1+0.27*0.8
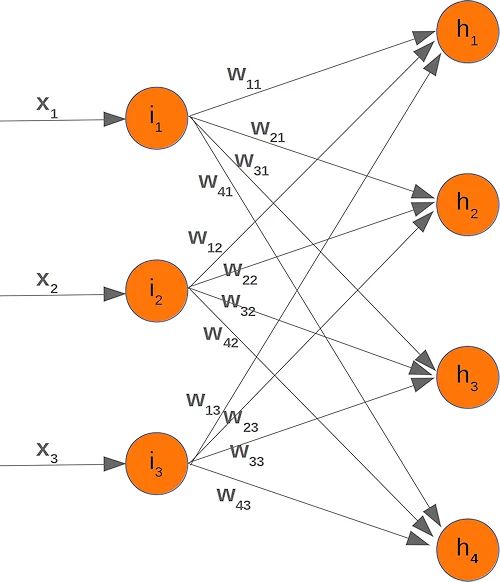
那些熟悉矩阵和矩阵乘法的人会看到它归结到什么地方。我们将重绘我们的网络并用瓦一世j:
为了有效地执行所有必要的计算,我们将权重排列成一个权重矩阵。上图中的权重构建了一个数组,我们将在神经网络类中将其称为“weights_in_hidden”。名称应表明权重连接输入和隐藏节点,即它们位于输入和隐藏层之间。我们还将名称缩写为“wih”。隐藏层和输出层之间的权重矩阵将表示为“who”:
现在我们已经定义了我们的权重矩阵,我们必须进行下一步。我们必须将矩阵与输入向量相乘。顺便提一句。这正是我们在前面的示例中手动完成的。
(是1是2是3是4)=(瓦11瓦12瓦13瓦21瓦22瓦23瓦31瓦32瓦33瓦41瓦42瓦43)(X1X2X3)=(瓦11⋅X1+瓦12⋅X2+瓦13⋅X3瓦21⋅X1+瓦22⋅X2+瓦23⋅X3瓦31⋅X1+瓦32⋅X2+瓦33⋅X3瓦41⋅X1+瓦42⋅X2+瓦43⋅X3)
对于隐藏层和输出层之间的“who”矩阵,我们有类似的情况。所以输出z1 和 z2 从节点 ○1 和 ○2 也可以用矩阵乘法计算:
(z1z2)=(瓦H11瓦H12瓦H13瓦H14瓦H21瓦H22瓦H23瓦H24)(是1是2是3是4)=(瓦H11⋅是1+瓦H12⋅是2+瓦H13⋅是3+瓦H14⋅是4瓦H21⋅是1+瓦H22⋅是2+瓦H23⋅是3+瓦H24⋅是4)
您可能已经注意到我们之前的计算中缺少某些内容。我们在介绍性的Python中从零开始的神经网络一章中展示了我们必须应用激活或阶跃函数Φ 在这些金额中的每一个。
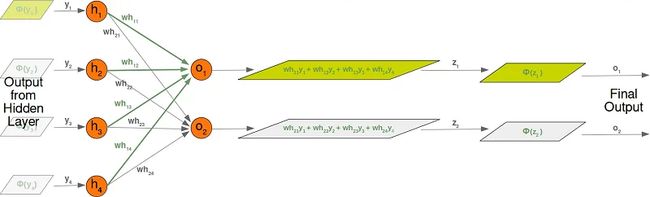
下图描述了整个计算流程,即矩阵乘法和激活函数的后续应用。
矩阵 wih 与输入节点值的矩阵之间的矩阵乘法X1,X2,X3 计算将传递给激活函数的输出。
最终输出 是1,是2,是3,是4 是权重矩阵的输入:
即使处理是完全模拟的,我们也会详细了解隐藏层和输出层之间发生的事情:
初始化权重矩阵
在训练神经网络之前必须做出的重要选择之一是初始化权重矩阵。当我们开始时,我们对可能的权重一无所知。那么,我们可以从任意值开始吗?
正如我们已经看到的,除了输入节点之外的所有节点的输入是通过将激活函数应用于以下总和来计算的:
是j=∑一世=1n瓦j一世⋅X一世
(n 是上一层的节点数, 是j 是下一层节点的输入)
我们可以很容易地看到,将所有权重值设置为 0 并不是一个好主意,因为在这种情况下,求和的结果将始终为零。这意味着我们的网络将无法学习。这是最糟糕的选择,但将权重矩阵初始化为 1 也是一个糟糕的选择。
权重矩阵的值应该随机选择,而不是任意选择。通过选择随机正态分布,我们打破了可能的对称情况,这可能并且通常对学习过程不利。
有多种方法可以随机初始化权重矩阵。我们将介绍的第一个是来自 numpy.random 的 unity 函数。它创建在半开区间 [low, high) 上均匀分布的样本,这意味着包括低而排除高。给定区间内的每个值都同样有可能被“统一”绘制。
将 numpy 导入为 np
number_of_samples = 1200
低 = - 1
高 = 0
s = np 。随机的。统一(低、 高、 number_of_samples )
#S的所有值是半开区间[-1,0)内:
打印(NP 。所有(小号 > = - 1 ) 和 NP 。所有(小号 < 0 ))
输出:
真的
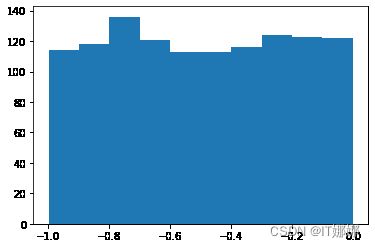
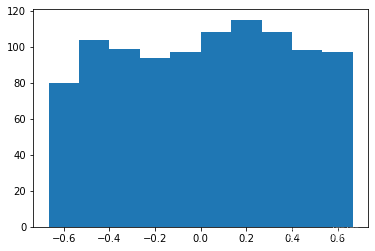
样本的直方图,在我们之前的例子中使用统一函数创建,如下所示:
我们将看到的下一个函数是来自 numpy.binomial 的“二项式”:
binomial(n, p, size=None)它从具有指定参数、n试验和p成功概率的二项式分布中抽取样本,其中n是整数>= 0,p是区间 [0,1] 中的浮点数。(n可以作为浮点数输入,但在使用中被截断为整数)
我们喜欢创建具有正态分布的随机数,但这些数字必须是有界的。np.random.normal() 不是这种情况,因为它不提供任何绑定参数。
为此,我们可以使用 scipy.stats 中的 truncnorm。
这种分布的标准形式是截断到 [a, b] 范围内的标准正态——注意 a 和 b 是在标准正态的域上定义的。要转换特定平均值和标准偏差的剪辑值,请使用:
a, b = (myclip_a - my_mean) / my_std, (myclip_b - my_mean) / my_std从 scipy.stats 导入 truncnorm
s = truncnorm ( a =- 2 / 3. , b = 2 / 3. , scale = 1 , loc = 0 ) . 房车(大小= 1000 )
PLT 。历史(S )
PLT 。显示()
函数“truncnorm”很难使用。为了让生活更轻松,我们truncated_normal在下面定义了一个函数来简化这个任务:
def truncated_normal ( mean = 0 , sd = 1 , low = 0 , upp = 10 ):
return truncnorm (
( low - mean ) / sd , ( upp - mean ) / sd , loc = mean , scale = sd )
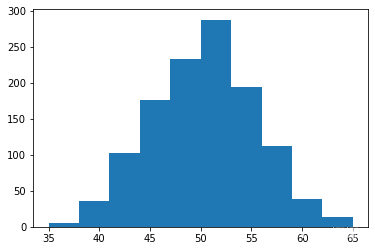
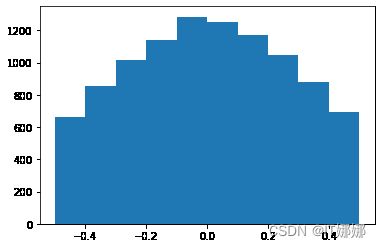
X = truncated_normal (平均值= 0 , SD = 0.4 , 低= - 0.5 , UPP = 0.5 )
小号 = X 。房车( 10000 )
PLT 。历史(S )
PLT 。显示()
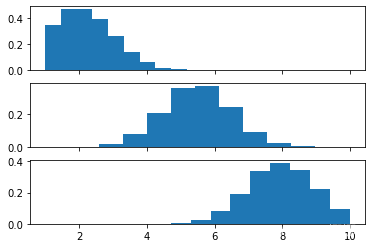
进一步的例子:
X1 = truncated_normal (平均值= 2 , SD = 1 , 低= 1 , UPP = 10 )
X2 = truncated_normal (平均值= 5.5 , SD = 1 , 低= 1 , UPP = 10 )
X3 = truncated_normal (平均值= 8 , SD = 1 , 低= 1 , 向上= 10 )
导入 matplotlib.pyplot 作为 plt
fig , ax = plt 。子图( 3 , sharex = True )
ax [ 0 ] 。hist ( X1 . rvs ( 10000 ), density = True )
ax [ 1 ] 。hist ( X2 . rvs ( 10000 ), 密度= True )
ax [ 2] 。hist ( X3 . rvs ( 10000 ), 密度= True )
plt . 显示()
我们现在将创建链接权重矩阵。truncated_normal是此目的的理想选择。从区间内选择随机值是个好主意
(-1n,1n)
其中 n 表示输入节点的数量。
所以我们可以创建我们的“wih”矩阵:
no_of_input_nodes = 3
no_of_hidden_nodes = 4
rad = 1 / np 。sqrt ( no_of_input_nodes )
X = truncated_normal ( mean = 2 , sd = 1 , low =- rad , upp = rad )
wih = X 。RVS ((no_of_hidden_nodes , no_of_input_nodes ))
王氏
输出:
数组([[-0.3053808, 0.5030283, 0.33723148],
[-0.56672167, -0.35983275, 0.22429119],
[ 0.29448907, 0.23346339, 0.42599121],
[ 0.30590101, 0.47121411, 0.07944389]])
同样,我们现在可以定义“who”权重矩阵:
no_of_hidden_nodes = 4
no_of_output_nodes = 2
rad = 1 / np 。sqrt ( no_of_hidden_nodes ) # 这是这一层的输入!
X = truncated_normal ( mean = 2 , sd = 1 , low =- rad , upp = rad )
who = X 。房车((no_of_output_nodes , no_of_hidden_nodes ))
谁
输出:
数组([[-0.31382676, 0.28733613, -0.11836658, 0.29367762],
[ 0.45613032, 0.43512081, 0.30355432, 0.43769041]])