「Python数据分析」 社交网络:共现/合作网络(无向有权图) 生成邻接矩阵、共现矩阵
这里的共现矩阵矩阵就是对角线上是节点权重的邻接矩阵,我为了区分他们换个名字而已。
不过用矩阵存储网络空间利用率还是太低了,所以一般我还是把节点权重和节点存在一起,边的权重和边存在一起,再加上一个邻接表,就不生成邻接矩阵了,这篇文章只是对之前代码迭代过程的一个记录。不过如果以后遇到对数据格式有特殊要求的场景,我就得再去学学稀疏矩阵了…
以下是原文:
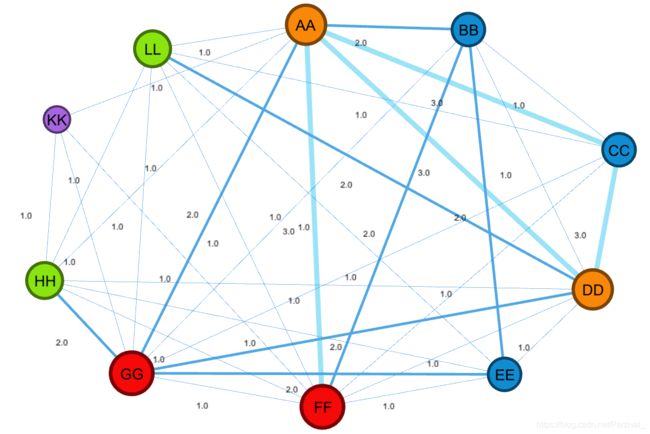
使用从数据库中导出的论文、专利数据,做作者/专利权人合作网络,实际上也就是共现网络。
存储网络的形式有很多种:邻接矩阵(matrix)、共现矩阵、节点列表(node list)、带权重的边列表(weighted edges)、边列表(edge list)、邻接表(adjacency list),主要还是根据自己后续的数据处理需求来选择存储结构。
其中节点列表、边列表可以作为G.add_nodes_from()、G.add_edges_from()的输入,带权重的边列表可以作为networkx中G.add_weighted_edges_from()方法的输入。节点列表、合作矩阵(邻接矩阵)、边列表、邻接表还可以作为各种网络绘制软件的输入数据,比如Ucinet、Gephi。
本文记录邻接矩阵、共现矩阵生成方式,其他方式可参考:
生成节点、边列表 、 生成边-权重列表、生成邻接表
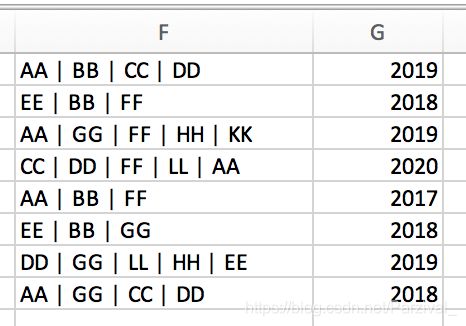
使用的数据形式示例:
合作网络构建
生成合作网络代码主函数:
if __name__ =='__main__' :
co_list = [ ["AA | BB | CC | DD",2019],
["EE | BB | FF ",2018],
["AA | GG | FF | HH | KK",2019],
["CC | DD | FF | LL | AA",2020],
["AA | BB | FF ",2017],
["EE | BB | GG ",2018],
["DD | GG | LL | HH | EE",2019],
["AA | GG | CC | DD",2018]]
# 1.获取节点列表
author_list = get_nodes(co_list,0)
# 2.合作矩阵(类似于邻接矩阵)
get_cooperate_matrix(author_list,0)
1. 提取出节点列表。
调用了自定义的函数get_nodes()。调用这两个函数之前要把原始数据提取到形如co_list的列表里。
函数实现如下:
获取节点列表:get_nodes():
获取所有出现的节点列表。
def get_nodes(co_list,col):
'''
rows: 形如co_list的所有用来构建合作网络的数据行
col: 作者信息所在列数-1
'''
nodes_list = []
for authors in co_list:
auths = authors[col].split(" | ") # 分隔符可换
for auth in auths:
if auth not in nodes_list: # 去重
nodes_list.append(auth)
return nodes_list
结果:
["AA","BB","CC","DD","EE","FF","GG","HH","KK","LL"]
2. 生成共现矩阵(对角线上是节点权重)
调用自定义的函数get_cooperate_matrix(),实现方法如下。
合作矩阵:1. 直接通过节点列表+原始数据构建
最开始实现的时候用了很多字典结构存储每个作者的合作关系,运行的时候发现内存开销异常的大(电脑内存不够的卑微),因此最后全部改回列表形式。其实这里没有涉及到大量数据搜索,所以使用字典的意义也不大,不能节省时间,反而增加内存占用。
def get_cooperate_matrix1(rows,nodes_list,col):
'''
rows: 形如co_list的所有用来构建合作网络的数据行
nodes_list: 节点列表
col: 节点共现信息所在列数-1
'''
length = len(nodes_list)
cooperate_list = []
# 遍历作者名,计数和各作者合作数(每次合作对自己也计数)
for node in nodes_list:
node_co = []
node_co.append(node)
# 合作列表:初始化为长度为节点个数的全零列表[name,0,0,0,...,0,0]
for i in range(length):
node_co.append(0)
# 遍历所有数据行,对作者字段进行匹配
for row in rows:
nodes = row[col].split(" | ") # 分隔符按数据结构选
# 对包含当前节点的数据项,提取共现关系(合作列表对应位置+1)
if node in nodes:
for each_node in nodes:
# 索引共现的节点编号,确定在合作列表中的位置
node_index = nodes_list.index(each_node)+1
# 对应位置+1
node_co[node_index] = node_co[node_index] + 1
# 添加到合作矩阵列表中
cooperate_list.append(node_co)
# 1. 生成合作矩阵:cooperate_mat
cooperate_mat = []
first_line = ['']
first_line.extend(nodes_list)
cooperate_mat.append(first_line) # 第一行,第一列为标题(出现的作者名)
cooperate_mat.extend(cooperate_list)
return cooperate_mat
写入操作这里就省略了,可以参照 csv文件写入。
共现矩阵:2. 通过节点列表+边列表构建
生成节点列表、边列表方法:get_nodes_edges()
def get_cooperate_matrix2(nodes_list,edge_list):
'''
nodes_list:节点列表
edge_list: 边列表
'''
length = len(nodes_list)
cooperate_list = []
for node in nodes_list:
node_co = []
node_co.append(node)
# 合作列表:初始化为长度为节点个数的全零列表[node,0,0,0,...,0,0]
for i in range(length):
node_co.append(0)
# 遍历所有边,对节点进行匹配
for edge in edge_list:
# 对包含当前节点的边,提取共现关系(合作列表对应位置+1)。对角线上为当前节点总次数。
if node in edge:
for each_node in edge:
# 索引节点编号,确定在合作列表中的位置
node_index = nodes_list.index(each_node)+1
# 对应位置+1
node_co[node_index] = node_co[node_index] + 1
cooperate_list.append(node_co)
# 合并各节点数据,生成合作矩阵。
cooperate_mat = []
first_line = ['']
first_line.extend(nodes_list)
cooperate_mat.append(first_line)
cooperate_mat.extend(cooperate_list)
return cooperate_mat
结果
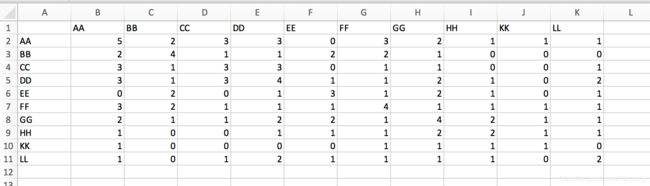
合作矩阵(类似邻接矩阵):
对角线上是对应节点的总共出现次数,其他位置为共现次数(权重)。
3.生成邻接矩阵(对角线上为0)
生成“边-权重”列表方法: 生成边-权重列表
def get_adjacency_matrix(node_list,weighted_links):
'''
nodes_list:节点列表(sorted)
edge_list: 边-权重列表
'''
# 初始化adjacency_mat为全零矩阵
adjacency_mat = [[0 for val in range(len(node_list))] for val in range(len(node_list))]
for x, y, val in weighted_links:
i = node_list.index(x)
j = node_list.index(y)
adjacency_mat[i][j] = adjacency_mat[j][i] = val
return adjacency_mat
结果
除了对角线全为0,其它和共现矩阵一样。