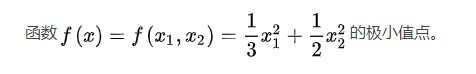机器学习数学基础梯度下降法之Python矩阵运算
文章目录
-
-
- 一、梯度下降法的原理介绍
-
- (一)梯度下降法
- (二)梯度下降的相关概念及描述
- (三)梯度下降算法原理
- 二、梯度下降法的一般求解步骤
- 三、梯度下降法手工求解极值
- 四、Excel中利用梯度下降求解近似根
- 五、线性回归问题求解
-
- (一)最小二乘法
- (二)梯度下降
- 参考链接
-
一、梯度下降法的原理介绍
(一)梯度下降法
梯度下降(gradient descent)主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。所以,它是一种常用的求解无约束最优化问题的方法,在最优化、统计学以及机器学习等领域有着广泛的应用。
(二)梯度下降的相关概念及描述
-
下山过程描述
场景描述:一个人需要从山的某处开始下山,尽快到达山底。
下山过程重要的信息:方向和距离
为了尽快的到达山底,需要选择最陡峭的方向下山。而且,在下山的过程中,下山方向也并不是一层不变的,每过一段距离,就需要重新选择方向。

-
梯度下降的过程内容描述
梯度下降的过程跟下山过程很相似。两者结合来看,山就等同于我们需要优化的函数表达式,山的最低点就等同于我们求解的最优值,而每次下山的距离就是梯度下降中的学习率,寻找方向利用的信息就是样本数据,某处就是优化函数设置的初始值。
求解最优解的过程,就是利用初始值不断迭代求解得到的。
补充:
α(步长/学习率)取值不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点。
(三)梯度下降算法原理
- 批量梯度下降法(Batch Gradient Descent, BGD)
批量梯度下降法在计算优化函数的梯度时利用全部样本数据,n表示总的样本数
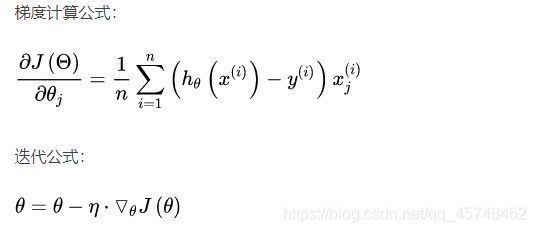
- 小批量梯度下降法(Mini-batch Gradient Descent, MBGD)
随机梯度下降法在计算优化函数的梯度时利用随机选择的一个样本数据

- 随机梯度下降法(Stochastic Gradient Descent, SGD)
小批量梯度下降法在计算优化函数的梯度时利用随机选择的一部分样本数据,k表示选取样本的数目
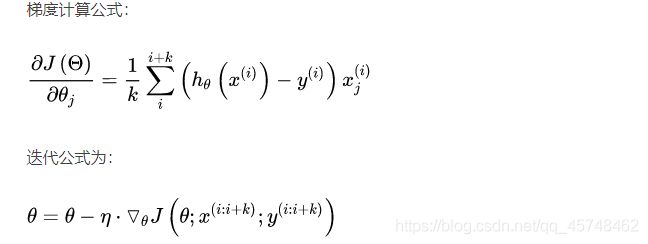
三种方式的优缺点

二、梯度下降法的一般求解步骤
三、梯度下降法手工求解极值
四、Excel中利用梯度下降求解近似根
求解 z = 2 ( x − 1 ) ^2 + y ^2 的近似根
- 设置表格的一些基本内容

- 设置(x,y)的初始值为(2,1)
- 其他表格输入相应的计算公式

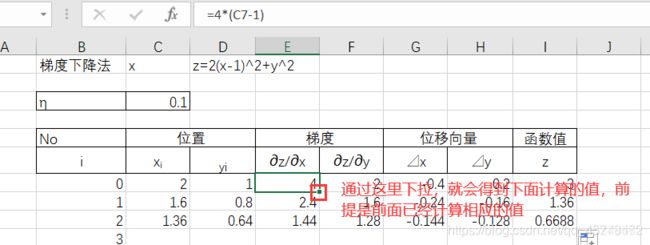
其他位置的按照公式输入相应的内容,然后安装从左向右的顺序,向下拉取多格 - 多次迭代结果
当学习率取0.1的时候,迭代2000多次仍旧没有出现函数值为0的情况,所以更改学习率为0.15
结果

由此,可得到其近似值为(1,0),迭代很多次才得到想要的结果。
五、线性回归问题求解
(一)最小二乘法
- 代码
定义数据及设置相关数值
from sklearn import linear_model
#可以调用sklearn中的linear_model模块进行线性回归
import seaborn as sns
# 定义数据集的大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,其值全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
Y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
进行线性回归
#进行线性回归的求解
model = linear_model.LinearRegression()
model.fit(X1,Y)
print("斜率=",model.coef_[0])
print("截距为=",model.intercept_)
# 根据数据画出对应的图像
def plot(X, Y, theta):
ax = plt.subplot(111) # 将画布分为1行1列,取第一个
ax.scatter(X, Y, s=30, c="blue", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = model.intercept_+ model.coef_[0]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, model.coef_[0])
(二)梯度下降
from numpy import *
# 定义数据集的大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1)) # 生成一个m行1列的向量,其值全是1
X1 = arange(1, m+1).reshape(m, 1) # 生成一个m行1列的向量,也就是x1,从1到m
X = hstack((X0, X1)) # 按照列堆叠形成数组,其实就是样本数据
# 对应的y坐标
Y = np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01
import matplotlib.pyplot as plt
#绘制出数据集
plt.scatter(X1,Y,color='red')
plt.show()
# 定义代价函数
#损失函数(loss function)或代价函数(cost function)是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数
def cost_function(theta, X, Y):
diff = dot(X, theta) - Y # dot() 数组需要像矩阵那样相乘,就需要用到dot()
return (1/(2*m)) * dot(diff.transpose(), diff)
# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
diff = dot(X, theta) - Y
return (1/m) * dot(X.transpose(), diff)
梯度下降迭代
# 梯度下降迭代
def gradient_descent(X, Y, alpha):
#将[1,1]变为2行1列的形式
theta = array([1, 1]).reshape(2, 1)
#得到代价函数的初始梯度
gradient = gradient_function(theta, X, Y)
#不断迭代的过程
while not all(abs(gradient) <= 1e-5):
#更新迭代公式
theta = theta - alpha * gradient
#更新迭代所用的梯度
gradient = gradient_function(theta, X, Y)
return theta
#梯度下降最终的结果
optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
# 根据数据画出对应的图像
def plot(X, Y, theta):
ax = plt.subplot(111) # 将画布分为1行1列,取第一个
ax.scatter(X, Y, s=30, c="red", marker="s")
plt.xlabel("X")
plt.ylabel("Y")
x = arange(0, 21, 0.2) # x的范围
y = theta[0] + theta[1]*x
ax.plot(x, y)
plt.show()
plot(X1, Y, optimal)
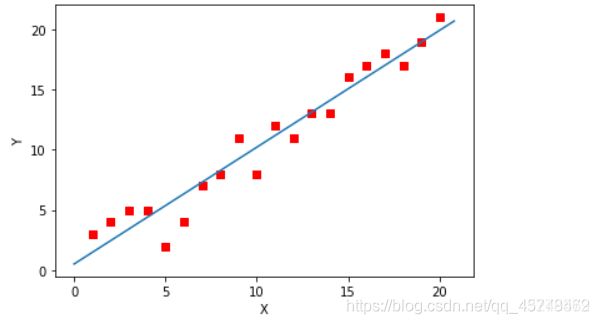
结论 :两个最终得到的结果相差极其小,小到差距可以被忽略。从代码量来说,最小二乘法是直接调用sklearn中linear_model.LinearR egression()来进行求解的,相对于梯度下降的方法来说,会更加快计算出结果。通过这个方法,还是比较好理解梯度下降的整个原理过程的实现。
参考链接
梯度下降算法原理讲解——机器学习
详解:如何用Python实现机器学习算法(1)
机器学习算法:梯度下降法——原理篇
深入浅出–梯度下降法及其实现
梯度下降法——极值,线性回归,近似根问题