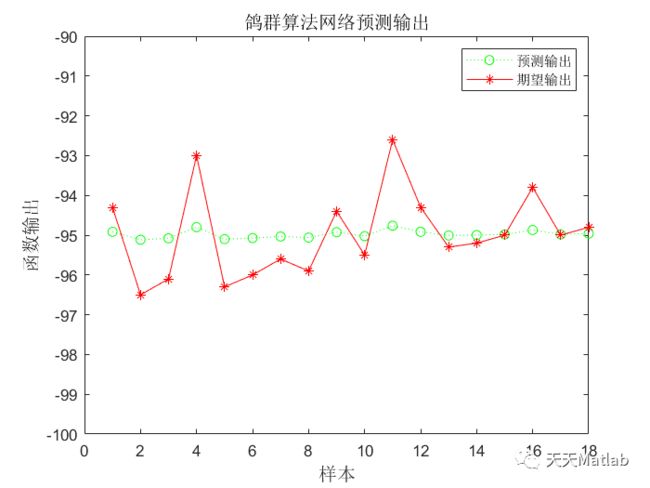
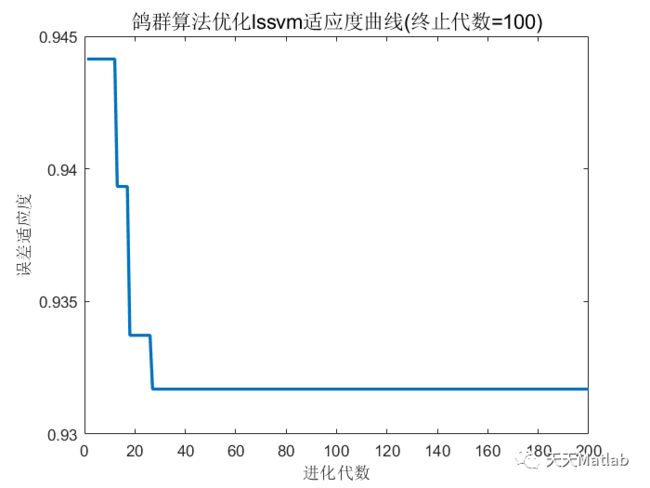
【lssvm回归预测】基于鸽群算法优化最小二乘支持向量机PIO-lssvm实现数据回归预测附matlab代码

​✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

LSSVM 模型中的参数选择对模型的影响较大,采用鸽群优化算法进行模型参数的全局选优,用历史负荷数据和天气气象因素作为输入,建立优化电力负荷预测模型进行仿真.利用 PIO- LSSVM 模型对华东某市电力负荷进行验证分析.实验结果表明:鸽群算法优化的LSSVM 模型相比 LSSVM 具有更高的预测精度.

⛄ 部分代码

function [Best_vulture1_F,Best_vulture1_X,convergence_curve]=PIO(pigeonnum,max_iter,lower_bound,upper_bound,D,fobj);

%%####A new bio-inspired swarm intelligence optimizer ?C pigeon inspired 

%%####optimization (PIO) is presented by simulating pigeons homing 

%%####behaviors. Homing pigeons can easily find their homes by using 

%%####three homing tools: magnetic field, sun and landmarks. In this  

%%#### newly invented algorithm, map and compass operator model is 

%%#### presented based on magnetic field and sun, while landmark operator 

%%#### model is presented based on landmarks. For some tough functions,  

%%#### it can quickly find the optimum, and it performs powerfully. For the 

%%#### most important reason, it combines some advantages of algorithms 

%%#### such as particle swarm optimization and artificial fish school algorithm. 

%***************initialization******************* 

T1=max_iter;     %Global search algebra 

T2=max_iter;     %Local search algebra 

% pigeonnum=30;    %number  

% D = 30;     % dimensionality 

R=0.3;     %parameters of magnetic field  

bound=[lower_bound,upper_bound];    %hunting zone

tol = 1e-7;

%**************initialization of the individual pigeon************ 

for i=1:pigeonnum                                                           %时间复杂度O(pigeonum*D*2)

    for j=1:D 

        x(i,j)=bound(1)+rand*(bound(2)-bound(1)); 

        v(i,j)=rand; 

    end 

end 

%**************calculate the fitness of pigeon*********** 

for i=1:pigeonnum                                                           %时间复杂度O(pigeonum*2)

    p(i)=fobj(x(i,:)); 

    p_best(i,:)=x(i,:); 

end 

%**************find the optimal pigeons******************** 

g_best=x(1,:); 

for i=2:pigeonnum                                                           %时间复杂度O(pigeonum-1)

    if fobj(g_best)>fobj(x(i,:)) 

        g_best=x(i,:); 

    end 

end 

%************  magnetic compass and solar operator******************** 

for t=1:T1                                                                  %时间复杂度O(T1*(pigeonum*(2D+5))+1)

    for i=1:pigeonnum                                                       %时间复杂度O(pigeonum*(2D+5))                       

        v(i,:)=v(i,:)+rand*(p_best(i,:)-x(i,:)); 

        x(i,:)=x(i,:)*(1-exp(-R*t))+v(i,:);   %check whether beyond the searching space 

        for j=1:D                                    % magnetic field and solar operator 

            if abs(i-1)<=eps 

                if x(i,j)bound(2) 

                    x(i,j)=bound(1)+rand*(bound(2)-bound(1)); 

                    v(i,j)=rand; 

                end 

            else 

                if x(i,j)bound(2) 

                    x(i,j)=x(i-1,j);  

                    v(i,j)=v(i-1,j); 

                end     

            end 

        end 

        if fobj(x(i,:))

            p(i)=fobj(x(i,:)); 

            p_best(i,:)=x(i,:); 

        end 

        if p(i)

            g_best=p_best(i,:); 

        end

    end

    result(t)=fobj(g_best); 

end 

%*************???????********************** 

for t=1:T2                                                                  %时间复杂度O(T2*pigeonum*pigeonum)

    for i=1:pigeonnum-1                             %sort the pigeons       

        for j=i+1:pigeonnum 

            if fobj(x(i,:))>fobj(x(j,:)) 

                temp_pigeon=x(i,:); 

                x(i,:)=x(j,:); 

                x(j,:)=temp_pigeon; 

            end 

        end 

    end 

    pigeonnum=ceil(pigeonnum/2);               %remove half of the pigeons according to the landmark 

    addpigeonnum=0;                        

    for i=1:pigeonnum 

        addpigeonnum=addpigeonnum+x(i,:);      

        p(i)=fobj(x(i,:));                     %calculate fitness and location of the pigeon after sorting 

        p_best(i,:)=x(i,:); 

    end 

    pigeoncenter=ceil(addpigeonnum./pigeonnum);%calculate central position 

    for i=1:pigeonnum                                %local searching        

        for j=1:D                                    %check whether beyond the searching space 

            x(i,j) = x(i,j) + rand*(pigeoncenter(j)-x(i,j));

            while x(i,j)bound(2)

                x(i,j) = x(i,j) + rand*(pigeoncenter(j)-x(i,j));

            end

        end 

        if fobj(x(i,:))

            p(i)=fobj(x(i,:)); 

            p_best(i,:)=x(i,:); 

        end 

        if p(i)

            g_best=p_best(i,:); 

        end 

    end 

    result(t+T1)=fobj(g_best);

end 

% figure                                               %graph 

% for t=1:T1+T2-1 

%     plot([t,t+1],[result(t),result(t+1)]); 

%     hold on; 

% end

% xlabel('Iterative curve');

% ylabel('Function value');

% title(['The best value is ' num2str()])

[Best_vulture1_F,indx]=min(result);

Best_vulture1_X=g_best;

convergence_curve=result;

end

⛄ 运行结果

⛄ 参考文献

[1]鞠彬王嘉毅. 基于粒子群算法与最小二乘支持向量机的ET0模拟[J]. 水资源保护, 2016, 32(4):74-79.

[2]吴文江, 陈其工, and 高文根. "基于 PSO 优化参数的最小二乘支持向量机短期负荷预测." 重庆理工大学学报（自然科学版） 030.003(2016):112-115.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料