python：激活函数及其导数画图sigmoid/tanh/relu/Leakyrelu/swish/hardswish/hardsigmoid

from matplotlib import pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def dx_sigmoid(x):
    return sigmoid(x) * (1 - sigmoid(x))


def tanh(x):
    return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
def dx_tanh(x):
    return 1-tanh(x)*tanh(x)

def relu(x):
    return np.maximum(0,x)#np.where(x < 0, 0, x)
def dx_relu(x):
    return np.where(x < 0, 0, 1)


def Leaky_relu(x,alpha):# a大于1，指定a
    return np.where(x<0,x/alpha,x)#np.maximum(x/alpha,x) #np.where(x<0,x/alpha,x)
def dx_Leaky_relu(x,alpha):
    return np.where(x < 0, 1/alpha, 1)

def swish(x,b):
    return x * (np.exp(b * x) / (np.exp(b * x) + 1)) #sigmoid(bx) * x
def dx_swish(x,b):
    return  np.exp(b*x)/(1+np.exp(b*x)) + x * (b*np.exp(b*x) / ((1+np.exp(b*x))*(1+np.exp(b*x))))#sigmoid(bx)+sigmoid(bx)*b*x



def hard_swish(x):
    f = x + 3
    relu6 = np.where(np.where(f < 0, 0, f) > 6, 6, np.where(f < 0, 0, f))
    return x * relu6 / 6
def dx_hard_swish(x):
    f = x + 3
    relu6 = np.where(np.where(f < 0, 0, f) > 6, 6, np.where(f < 0, 0, f))
    relu6_grad = np.where(f > 6, 0, np.where(f < 0, 0, 1))
    return relu6 / 6 + x * relu6_grad / 6


def hard_sigmoid(x):
    f = (2 * x + 5) / 10
    return np.where(np.where(f > 1, 1, f) < 0, 0, np.where(f > 1, 1, f))
def dx_hard_sigmoid(x):
    f = (2 * x + 5) / 10
    return np.where(f > 0, np.where(f >= 1, 0, 1 / 5), 0)

if __name__ == '__main__':

###1#####
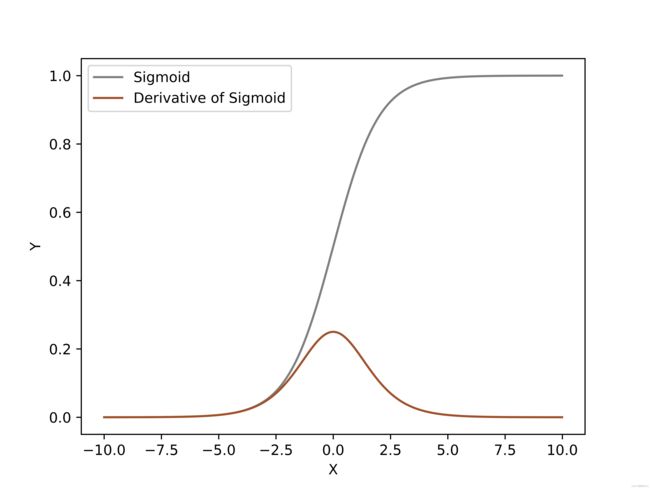
    x = np.arange(-10, 10, 0.01)
    fz = sigmoid(x)
    d_fz = dx_sigmoid(x)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(x, fz, color='grey',label='Sigmoid')
    plt.plot(x, d_fz,color='sienna',label='Derivative of Sigmoid')
    plt.legend()
    plt.savefig("Sigmoid.png", dpi=1000, format='png')
    plt.show()


###2#####
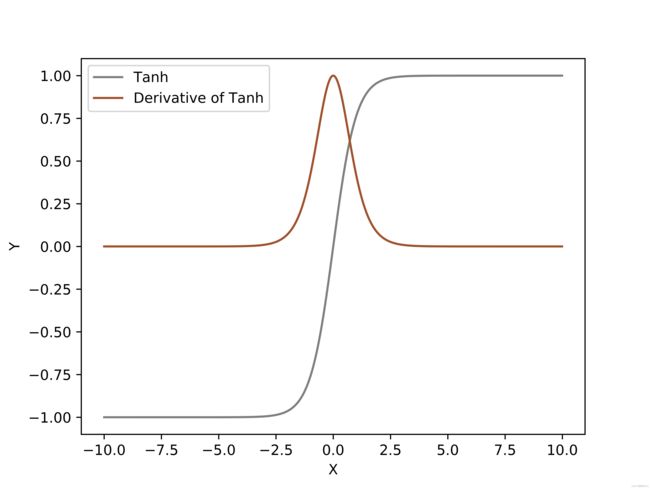
    y = np.arange(-10, 10, 0.01)
    fz = tanh(y)
    d_fz = dx_tanh(y)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(y, fz, color='grey',label='Tanh')
    plt.plot(y, d_fz,color='sienna',label='Derivative of Tanh')
    plt.legend()
    plt.savefig("Tanh.png", dpi=1000, format='png')
    plt.show()


###3#####
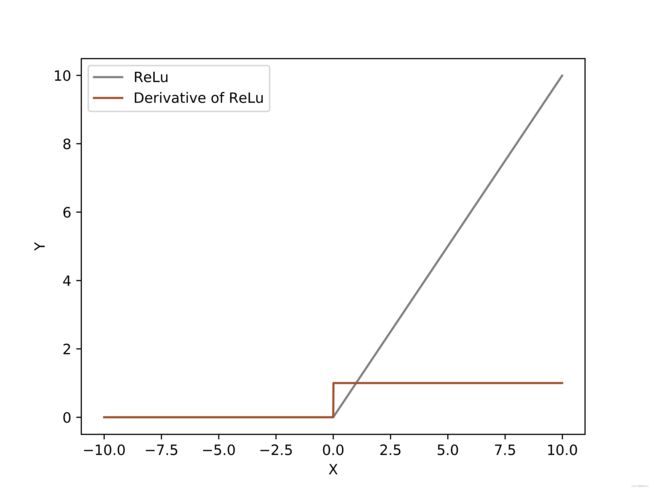
    z = np.arange(-10, 10, 0.01)
    fz = relu(z)
    d_fz = dx_relu(z)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(z, fz, color='grey',label='ReLu')
    plt.plot(z, d_fz,color='sienna',label='Derivative of ReLu')
    plt.legend()
    plt.savefig("ReLu.png", dpi=1000, format='png')
    plt.show()

###4#####
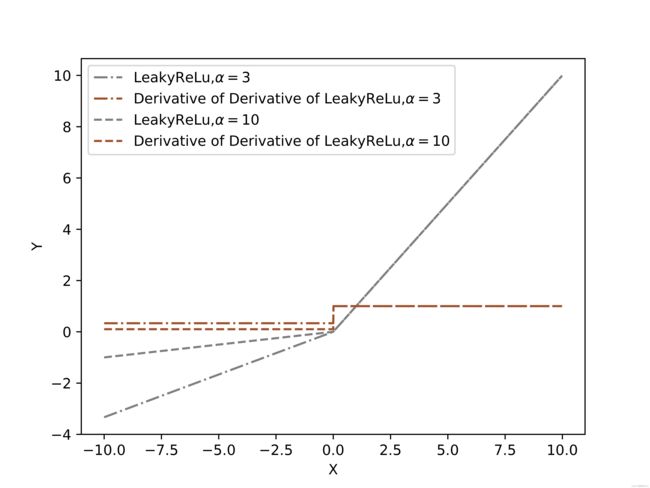
    p = np.arange(-10, 10, 0.01)
    fz = Leaky_relu(p,alpha=3)
    d_fz = dx_Leaky_relu(p,alpha=3)
    fx = Leaky_relu(p, alpha=10)
    d_fx = dx_Leaky_relu(p, alpha=10)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(p, fz, color='grey',linestyle='-.',label=r"LeakyReLu,$\alpha={0}$".format(3))
    plt.plot(p, d_fz,color='sienna',linestyle='-.',label=r"Derivative of Derivative of LeakyReLu,$\alpha={0}$".format(3))
    plt.plot(p, fx, color='grey', linestyle='--',label=r"LeakyReLu,$\alpha={0}$".format(10))
    plt.plot(p, d_fx, color='sienna',linestyle='--', label=r"Derivative of Derivative of LeakyReLu,$\alpha={0}$".format(10))
    plt.legend()
    plt.savefig("LeakyReLu.png", dpi=1000, format='png')  ###########保存原始图片
    plt.show()


###5#####
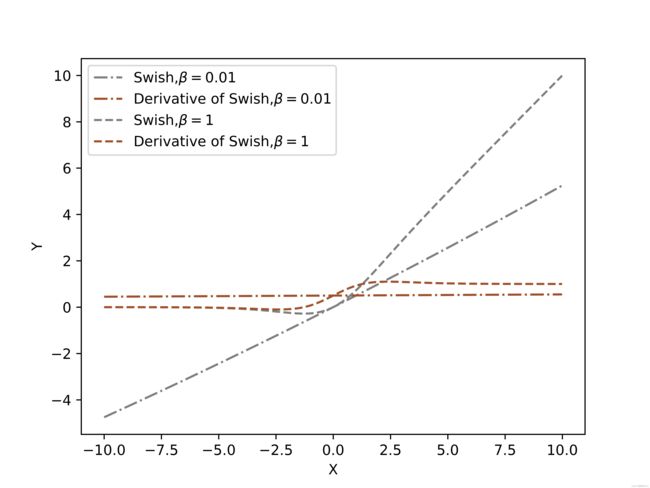
    g = np.arange(-10, 10, 0.01)
    fz = swish(g,b=0.01)
    d_fz = dx_swish(g,b=0.01)
    fy = swish(g,b=1)
    d_fy = dx_swish(g,b=1)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(g, fz, color='grey',linestyle='-.',label=r"Swish,$\beta={0}$".format(0.01))
    plt.plot(g, d_fz,color='sienna',linestyle='-.',label=r"Derivative of Swish,$\beta={0}$".format(0.01))
    plt.plot(g, fy, color='grey', linestyle='--',label=r"Swish,$\beta={0}$".format(1))
    plt.plot(g, d_fy, color='sienna', linestyle='--',label=r"Derivative of Swish,$\beta={0}$".format(1))
    plt.legend()
    plt.savefig("Swish.png", dpi=1000, format='png')  ###########保存原始图片
    plt.show()


###6#####
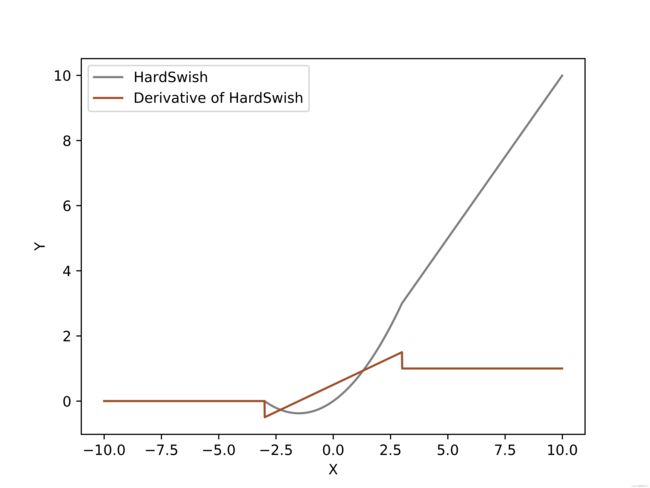
    f = np.arange(-10, 10, 0.01)
    fz = hard_swish(f)
    d_fz = dx_hard_swish(f)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(f, fz, color='grey',label='HardSwish')
    plt.plot(f, d_fz,color='sienna',label='Derivative of HardSwish')
    plt.legend()
    plt.savefig("HardSwish.png", dpi=1000, format='png')
    plt.show()


###7#####
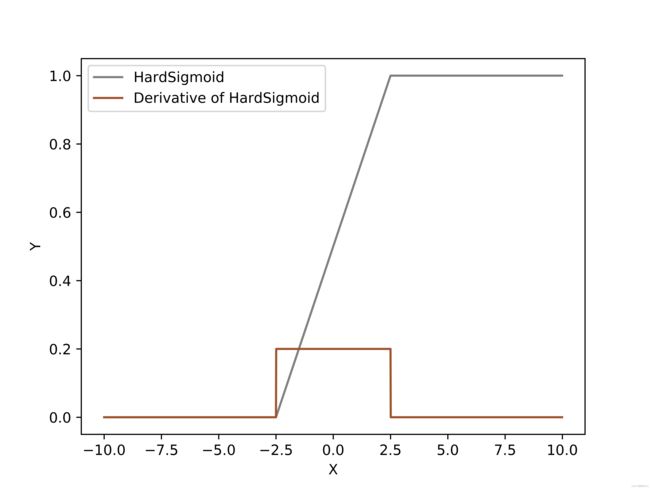
    k = np.arange(-10, 10, 0.01)
    fz = hard_sigmoid(k)
    d_fz = dx_hard_sigmoid(k)
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.plot(k, fz, color='grey',label='HardSigmoid')
    plt.plot(k, d_fz,color='sienna',label='Derivative of HardSigmoid')
    plt.legend()
    plt.savefig("HardSigmoid.png", dpi=1000, format='png')
    plt.show()

1.

2

3

4

5

6

7