三维空间直角坐标系转换（2）——改进七参数小旋转角的局限

前言：在之前的坐标系转换中，使用七参数模型只对小旋转角的坐标转换有作用，因此需要改进七参数模型，使其适应大旋转角，emm，我在这里借鉴了两位武大大佬的论文里的思路（武大不愧为测绘第一院校啊，人才真多），在这里引用一下。

[1]刘磊,何占国,郑作亚,贾传亮.大角度三维坐标转换参数的一种迭代解法[J].测绘科学,2021,46(06):65-69+76.DOI:10.16251/j.cnki.1009-2307.2021.06.010.

[2]姚宜斌,黄承猛,李程春,孔建.一种适用于大角度的三维坐标转换参数求解算法[J].武汉大学学报(信息科学版),2012,37(03):253-256.DOI:10.13203/j.whugis2012.03.008.

这里主要实现第一篇论文中的算法。

1.实现大旋转角度的思路

由于布尔沙七参数模型只适用与小旋转，因此在要适用大旋转角度只要修改旋转矩阵即可。在原文中，提出了由反对称矩阵构成的罗德里矩阵R代替七参数的旋转矩阵，并证明了该矩阵具有旋转矩阵的特征，具体公式大家可以看原文。

2.程序实现

代码如下。

import numpy as np


# 定义一个函数Large Angle coordinate conversion
def LACC(oldXYZ, newXYZ):
    m = len(oldXYZ)
    if m < 3:
        print('少于三个点')
        return
    if len(oldXYZ) != len(newXYZ):
        print('控制点坐标数量不同')
        return
    # 初值
    k = 1
    T = np.array([0, 0, 0]).reshape((3, 1))
    a = b = c = 0
    # 提取原、新坐标系坐标，方面调用
    XA = np.array(oldXYZ)[:, 0]
    YA = np.array(oldXYZ)[:, 1]
    ZA = np.array(oldXYZ)[:, 2]
    XB = np.array(newXYZ)[:, 0]
    YB = np.array(newXYZ)[:, 1]
    ZB = np.array(newXYZ)[:, 2]
    # 权矩阵
    P = np.eye(3 * m)
    # 迭代参数差值的初值
    dTx = dTy = dTz = 2
    da = db = dc = 0.0001
    dk = 0.0001
    # 迭代，这里选择平移参数迭代差值小于1，旋转abc小于1e-5（作者原文为1e-8），k小于1e-5（原文1e-7）
    while dTx > 1 or dTy > 1 or dTz > 1 or da > 0.00001 or db > 0.00001 or dc > 0.00001 or dk > 0.00001:
        # 构造S，R矩阵
        S = np.array([0, -float(c), -float(b), float(c), 0, -float(a), float(b), float(a), 0]).reshape((3, 3))
        E = np.eye(3)
        R = npmulti((E + S), np.linalg.inv(E - S))
        # 构造B矩阵(3mx7)
        # L矩阵（3mx1)
        SE = npmulti(S, -1) + E
        B1 = np.zeros((3 * m, 3))
        B1[0:m, :] = SE[0, :]
        B1[m:2 * m, :] = SE[1, :]
        B1[2 * m:3 * m, :] = SE[2, :]
        B2 = np.zeros((3 * m, 4))
        L = np.zeros((3 * m, 1))
        for i in range(0, m):
            B2[i][1] = -k * ZA[i] - ZB[i] + T[2]
            B2[i][2] = -k * YA[i] - YB[i] + T[1]
            B2[i][3] = XA[i] - c * YA[i] - b * ZA[i]
            B2[m + i][0] = -k * ZA[i] - ZB[i] + T[2]
            B2[m + i][2] = k * XA[i] + XB[i] - T[0]
            B2[m + i][3] = c * XA[i] + YA[i] - a * ZA[i]
            B2[2 * m + i][0] = k * YA[i] + YB[i] - T[1]
            B2[2 * m + i][1] = k * XA[i] + XB[i] - T[0]
            B2[2 * m + i][3] = b * XA[i] + a * YA[i] + ZA[i]
            L[i] = -(k * XA[i] - k * c * YA[i] - k * b * ZA[i] - XB[i] + T[0] - c * YB[i] + c * T[1] - b * ZB[i] + b *
                     T[2])
            L[m + i] = -(
                    k * c * XA[i] + k * YA[i] - k * a * ZA[i] + c * XB[i] - c * T[0] - YB[i] + T[1] - a * ZB[i] + a * T[
                2])
            L[2 * m + i] = -(
                    k * b * XA[i] + k * a * YA[i] + k * ZA[i] + b * XB[i] - b * T[0] + a * YB[i] - a * T[1] - ZB[i] + T[
                2])
        B = np.c_[B1, B2]
        # 求解法方程x=(Bnn-1)*W
        Nbb = npmulti(B.T, P, B)
        W = npmulti(B.T, P, L)
        x = npmulti(np.linalg.inv(Nbb), W)
        dTx, dTy, dTz, da, db, dc, dk = x[0:7]
        T = T + np.array([float(dTx), float(dTy), float(dTz)]).reshape((3, 1))
        a += da
        b += db
        c += dc
        k += dk
    return T, R, float(k)


# 自己写的一个函数，可以实现任意个矩阵相乘，前提条件第一个参数a为矩阵（写判断很麻烦，不如制定规则）
def npmulti(a, *par):
    # a为矩阵
    multi = a
    for p in par:
        if isinstance(p, np.ndarray):
            multi = np.matmul(multi, p)
        elif isinstance(p, int) or isinstance(p, float):
            multi = np.dot(multi, p)
    return multi

3.计算结果

这里选择原文中的5对点进行测试，代码如下。

if __name__ == '__main__':
    oldXYZ = []
    newXYZ = []
    # 取原文中的5对点测试
    oldXYZ.append((108521, 96611, 101222))
    oldXYZ.append((108819, 99931, 101213))
    oldXYZ.append((108379, 99937, 101438))
    oldXYZ.append((108965, 101930, 101206))
    oldXYZ.append((108302, 101930, 101583))

    newXYZ.append((0, 0, 0))
    newXYZ.append((289, 3327, 0))
    newXYZ.append((-144, 3327, 216))
    newXYZ.append((444, 5327, 0))
    newXYZ.append((-222, 5327, 333))
    # 可以输出T R k参数的值
    T, R, k = LACC(oldXYZ, newXYZ)
    # 计算原坐标在新坐标系下的坐标，以第一个点为例
    XA = oldXYZ[0]
    x = T + npmulti(R, np.array(XA).reshape((3, 1)), k)
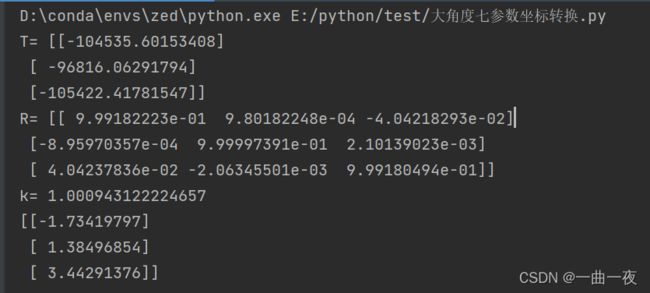
    print("T=", T, "\nR=", R, "\nk=", k)
    print(x)

结果如下。

4.分析 

首先，计算的矩阵与作者原文相似，但有差距，原因是控制点的个数不同，这里仅用了5个控制点，进行了3次迭代，同时使用5个点的单位权中误差也会大很多。

其次，计算的结果真实值为（0,0,0），第一个点的误差不大。当用其他点时，误差可能到达10mm甚至20mm，这就属于在那个点附近拟合精度差，要想提高精度只能加控制点了。

最后，emm，在摄影测量中，尽量能不转换坐标就不要转了，毕竟转换精度是一个问题。尽量用相对坐标就可以了。

坐标转换还有下一章。