day26【代码随想录】合并二叉树、二叉搜索树中的搜索、二叉搜索树中的插入操作、验证二叉搜索树、二叉搜索树中的众数、二叉搜索树中的最小绝对差

---

前言

1、合并二叉树
2、二叉搜索树中的搜索
3、二叉搜索树中的插入操作
4、验证二叉搜索树
5、二叉搜索树中的众数
6、二叉搜索树中的最小绝对差

---

一、合并二叉树（力扣617）

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

思路：
root1 =null return root2;
root2 =null return root1;
两个都不为空
值相加赋给新节点即可，左右结点同样操作

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1==null && root2!=null) return root2;
        else if(root1!=null && root2==null) return root1;
        else if(root1==null && root2==null) return null;

        //两棵树都不为空的情况
        TreeNode newRoot = new TreeNode();
        newRoot.val = root1.val + root2.val;
        newRoot.left = mergeTrees(root1.left,root2.left);
        newRoot.right = mergeTrees(root1.right,root2.right);
        return newRoot;
    }
}

二、二叉搜索树中的搜索（力扣700）

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

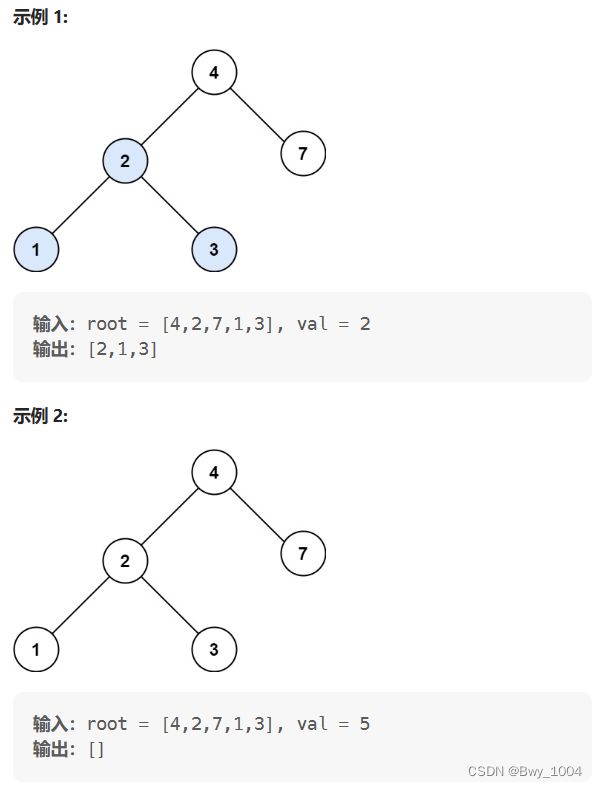
思路：
按照二叉搜索树的性质进行搜索，或者使用前中后层序依次遍历去搜索也可以

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root == null) return null;
        if(root.val>val){
            return searchBST(root.left,val);
        }
        else if(root.val<val){
            return searchBST(root.right,val);
        }else return root;

    }
}

三、二叉搜索树中的插入操作（力扣701）

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

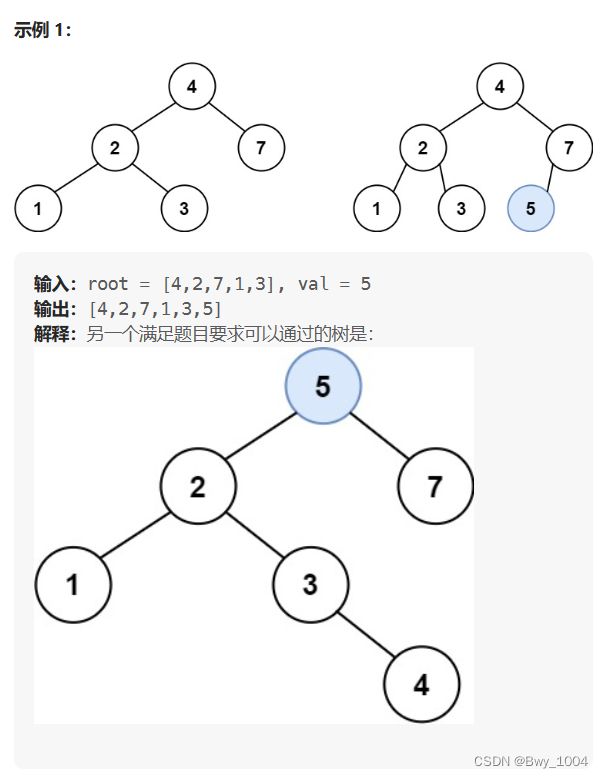
思路：
与上一题基本类似，先搜索再插入

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        TreeNode newNode = new TreeNode(val);
        if(root==null) return newNode;
        //查找插入的位置
        if(root.val>val){
            root.left = insertIntoBST(root.left,val);
        }else if(root.val<val){
            root.right = insertIntoBST(root.right,val);
        }
        return root;
    }
}

四、验证二叉搜索树（力扣98）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

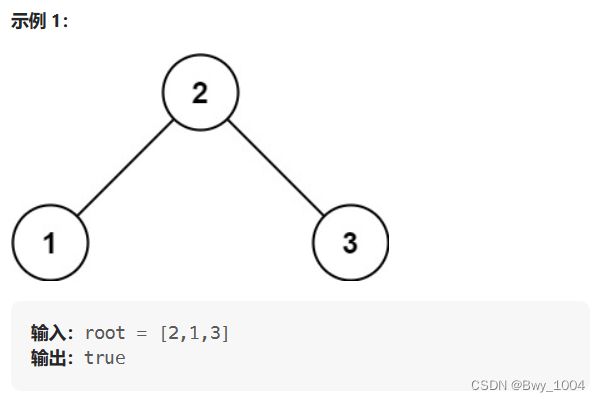
• 陷阱一：
  不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。

if (root->val > root->left->val && root->val < root->right->val) {
    return true;
} else {
    return false;
}

节点10大于左节点5，小于右节点15，但右子树里出现了一个6 这就不符合了！

• 陷阱二：
  样例中最小节点 可能是int的最小值，如果这样使用最小的int来比较也是不行的。
  链接: link

1、利用中序遍历

中序遍历会生成递增序列 然后每一次去处理结点的时候 和前一次的最大值去进行比较，如果比之前的值小说明不是二叉搜索树。

class Solution {
    private long prev = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        boolean leftBST = isValidBST(root.left);
        if(!leftBST) return false;
        if(root.val>prev){
            prev = root.val;
        }else return false;
        return isValidBST(root.right);
    }
}

2、双指针优化

class Solution {
    //private long prev = Long.MIN_VALUE;
    TreeNode max;
    public boolean isValidBST(TreeNode root) {
        if(root==null) return true;
        boolean leftBST = isValidBST(root.left);
        if(!leftBST) return false;
        if(max!=null &&root.val<=max.val){
            return false;
        }
        max = root;
        return isValidBST(root.right);
    }
}

五、二叉搜索树中的众数（力扣501）

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

思路：
双指针法

class Solution {
    TreeNode pre;
    int maxCount;
    int count;
    ArrayList<Integer> resList;

    public int[] findMode(TreeNode root) {
        resList = new ArrayList<>();
        maxCount =0;
        count =0;
        pre = null;
        traversal(root);
        int[] res = new int[resList.size()];
        for(int i=0;i<resList.size();i++){
            res[i] = resList.get(i);
        }
        return res;
    }

    public void traversal(TreeNode root){
        if(root==null) return ;
        traversal(root.left);
        if(pre==null) count=1;
        else if(pre.val==root.val) count++;
        else count=1;
        pre = root;
        if(count>maxCount){
            resList.clear();//清空之前的数据
            resList.add(root.val);
            maxCount = count;
        }else if(count==maxCount){
            resList.add(root.val);
        }
        traversal(root.right);
    }
}

六、二叉搜索树的最小绝对差（力扣530）

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

思路：
双指针法

1、递归法

class Solution {
    TreeNode pre;
    int res = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        //正常的遍历
        if(root==null) return 0;
        //左
        if(root.left!=null){
            getMinimumDifference(root.left);
        }
        //处理当前结点
        if(pre!=null && Math.abs(root.val-pre.val) < res){
            res = Math.abs(root.val-pre.val);
        }
        pre = root;
        //右
        if(root.right!=null){
            getMinimumDifference(root.right);
        }
        return res;
    }
}

2、迭代法

class Solution {
    TreeNode pre;
    Stack<TreeNode> stack;
    public int getMinimumDifference(TreeNode root) {
        if(root==null) return 0;
        stack = new Stack<>();
        TreeNode cur=root;
        int res = Integer.MAX_VALUE;
        while(cur!=null || !stack.isEmpty()){
            if(cur!=null){
                stack.push(cur);
                cur=cur.left;
            }else{
                cur = stack.pop();
                if(pre!=null){
                    res = Math.min(res,cur.val-pre.val);
                }
                pre=cur;
                cur=cur.right;
            }
        }
        return res;
    }
}

---

总结

中序遍历二叉搜索树等于遍历有序数组