Python课程设计（一）——线性回归的转化

线性回归的转化

一、课设要求

将一元线性回归示例xxhg.py改写成多元线性回归(由于多元线性回归不能在二维空间展示，将绘图部分删除）。

原代码（题目给定一元代码）如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

#%% 当噪声较小时
rng = np.random.RandomState(10)   # 设置随机局部种子
x =rng.normal(100,100,50)
x =x[:, np.newaxis]
y = 1.25 * x - 20 + 5 * rng.randn(50, 1)   # randn是标准正态分布

model = LinearRegression(fit_intercept=True)
model.fit(x, y)  # x,y的每一行是一个样本，即要求是列向量

x_fit = np.linspace(min(x), max(x), 1000)
#x_fit =x_fit[:, np.newaxis]
y_fit = model.predict(x_fit)
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
print('方程的判定系数(R^2): %.6f' % model.score(x, y))
plt.figure(figsize=(16, 12))
plt.scatter(x, y, s=10, c='k', marker='.')
plt.plot(x_fit, y_fit)
ax = plt.gca()
ax.set_aspect("equal")    # 纵横坐标单位相同
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.title('noise is samll')
plt.show()

#%% 当噪声较大时

rng = np.random.RandomState(10)   # 设置随机局部种子
x =rng.normal(100,100,50)
x =x[:, np.newaxis]
y = 1.25 * x - 20 + 100 * rng.randn(50, 1)   # 加大了噪声

model = LinearRegression(fit_intercept=True)
model.fit(x, y)  # x,y的每一行是一个样本，即要求是列向量

x_fit = np.linspace(min(x), max(x), 1000)
#x_fit =x_fit[:, np.newaxis]
y_fit = model.predict(x_fit)
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
print('方程的判定系数(R^2): %.6f' % model.score(x, y))
plt.figure(figsize=(16, 12))
plt.scatter(x, y, s=10, c='k', marker='.')
plt.plot(x_fit, y_fit)
ax = plt.gca()
ax.set_aspect("equal")    # 纵横坐标单位相同
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.title('noise is big')
plt.show()

二、实验原理

一元线性回归：是分析只有一个自变量（自变量x和因变量y）线性相关关系的方法。一个经济指标的数值往往受许多因素影响，若其中只有一个因素是主要的，起决定性作用，则可用一元线性回归进行预测分析。
多元线性回归：在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。事实上，一种现象常常是与多个因素相联系的，由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。因此多元线性回归比一元线性回归的实用意义更大。

三、实现过程

思路：首先构建一个50 * 3的矩阵，然后设置三个自变量分别为x1,x2,x3（x1,x2,x3 分别对应矩阵的一二三列），再将三组数据集转置成50行1列的矩阵，随机写出一个y关于x1,x2,x3 的多元方程并加入噪声，带入线性回归模型中拟合函数，将拟合后的x1,x2,x3 增加一个维度，再将三个数组进行垂直堆叠为一个数组，并预测拟合y，输出拟合后预测的变量系数、截距、和拟合回归的准确度

四、程序运行结果：

具体代码如下：

import numpy as np
from sklearn.linear_model import LinearRegression
#%% 当噪声较小时
rng = np.random.RandomState(10)   # 设置随机局部种子
x =rng.normal(100,100,50) 
x =100 * rng.rand(50, 3)  
x1=x[:,0]
x1.shape=50,1
x2=x[:,1]
x2.shape=50,1
x3=x[:,2]
x3.shape=50,1  
y = 1.25*x1+2.5*x2+3*x3+10+rng.randn(50,1) # randn是标准正态分布 
model = LinearRegression(fit_intercept=True) #是否求截距
model.fit(x, y)  # x,y的每一行是一个样本，即要求是列向量
a = np.linspace(0,50,1000)    #从0到50创建1000个等差数列
x1_fit= a[:,np.newaxis]       #将a转置成列
x2_fit =a[:,np.newaxis]       #fit函数用于拟合数据的输入输出 用来分析模型参数
x3_fit =a[:,np.newaxis]            
x_fit = np.hstack((x1_fit,x2_fit,x3_fit))    #将x1，x2，x3合并一起
y_fit = model.predict(x_fit)      #根据x对y的预测
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)#截距
print('方程的判定系数(R^2): %.2f' % model.score(x, y))

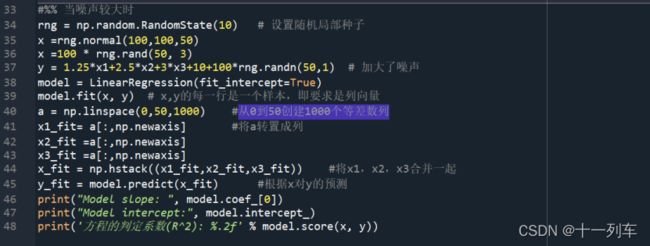
#%% 当噪声较大时
rng = np.random.RandomState(10)   # 设置随机局部种子
x =rng.normal(100,100,50)
x =100 * rng.rand(50, 3)
y = 1.25*x1+2.5*x2+3*x3+10+100*rng.randn(50,1)  # 加大了噪声
model = LinearRegression(fit_intercept=True)
model.fit(x, y)  # x,y的每一行是一个样本，即要求是列向量
a = np.linspace(0,50,1000)    #从0到50创建1000个等差数列
x1_fit= a[:,np.newaxis]       #将a转置成列
x2_fit =a[:,np.newaxis]
x3_fit =a[:,np.newaxis]
x_fit = np.hstack((x1_fit,x2_fit,x3_fit))    #将x1，x2，x3合并一起
y_fit = model.predict(x_fit)      #根据x对y的预测
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
print('方程的判定系数(R^2): %.2f' % model.score(x, y))