汉明编码及其应用——你看这一篇就够了！！！！

吹水

刚刚开始学计组，汉明码，什么玩意。。被折磨了好久，知道弄懂了之后，无法用言语来表达到底有多妙，真是妙蛙种子吃着妙脆角妙进了米奇妙妙屋妙到家了。

汉明码【来自某百科】

汉明码：汉明码（Hamming Code），是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码，当计算机存储或移动数据时，可能会产生数据位错误，以侦测并更正单一比特错误。由于汉明编码简单，它们被广泛应用于内存【某百科的介绍】，这谁看得懂。。所以，还是得靠自己摸索。。。

---

字符出错的概率

一个字符串传输过程中，如果该字符串出错了，那么只出错一个字符的概率为90%，出错两个或者两个以上的概率远小于值出错一个的概率。

---

奇校验和偶校验

首先，我们得先理解一下什么是奇校验，什么是偶校验。
举个栗子：我们传输一个字符串，比如 01010101110。。。。。
如果采用奇校验，就是加上一个校验位【可0可1】，使得代码串中1的个数为奇数个
如果采用偶校验，就是加上一个校验位【可0可1】，使得代码串中1的个数为偶数个

比如 我们要传输这个字符串：00100011这个字符串，如果我们采用偶校验，那就是100100011，那么就使得1的个数为偶数个。如果这时我们读出来的字符串是中1的个数是奇数个，那么就说明有一个字符出错了。【一个字符出错的概率远远大于两个字符出错的概率，大概90%的出错都是一个字符出错】

我们还可以更加精细划分，知道出错的区域。【如下】，但是，汉明码是一种非划分方式。组合组之间是有交叉的

汉明码的作用

汉明码是具有一位纠错能力的编码 ，也就是说，只能检验一位错误，是检查不了两位的。

---

过程详解

比如：我们现在有1-7共7位数据，我们分为三组，所以有三位校验位，四位数据位。

上面讲到，汉明码是一种非划分方式的编码，组合组之间是有交叉的。每个圆圈表示一组，1,2,4被单独分到了每一组中，这种分组的好处：总共三组，每一组假设都采用偶校验的方式，每组都包含4位数据，四位数据有一位校验位，保证该组1的个数为偶数个。

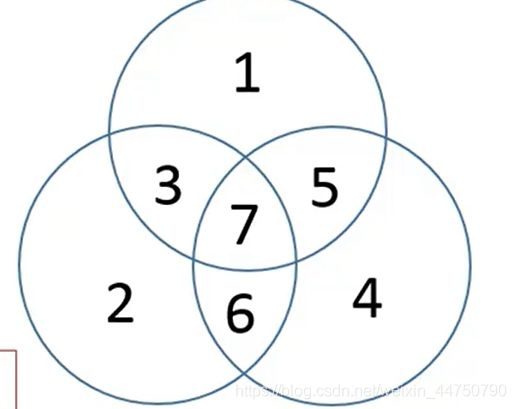
下面，如果我们接收到了的数据，每一组都是偶数个1，那一般是没错的【上面讲了，同时两个字符出错的概率远小于一个字符出错的概率（大概为90%）】。

汉明码使用

但是我们要想知道传输的结果对不对，就需要对每一组进行校验。我们使用p1来表示第一组的校验结果，使用p2来表示第二组的校验结果，使用p3来表示第三组的校验结果。出错结果记为1，没出错结果记为0.

---

假设结果如下：

1.如果结果为000，那就没差错了【二级制转化为十进制结果为0】
2.如果结果为001，那么就表示，第一组出错了，那第一组谁错了呢？肯定是第一组独有的那个数字错了，所以，1的位置的编码，是错误的。【二进制转化为十进制结果为1】
3.如果结果为101，那么就表示，第一组和第三组结果都是出错了，那就找到第一组和第三组共有的位置，编号5的是编码错误的【二进制转化为十进制结果为5】
4.如果是111，那就是三组都出错了，那就是位置7的编码错误了。【二级制转化为是十进制，结果为7】
通过以上这样，我们就可以发现，到底是哪个位置的编码错误了。【因为每次都只能发现一位编码错误，所以这就是汉明码为什么是具有一位纠错能力的编码】
还有，如果我们把结果的二进制转化为十进制，会发现对应的数值刚刚好是出错的编码字符的位置。

谁是校验码？校验位的位置在哪？

校验位：校验位是只对一组数据进行校验，所以绝不会与其他组共有。所以只能是1,2,4【上面的绿字有点到】。
所以，校验位的位置就是2的n次方【1,2,4,8,16。。。】

---

第一次感慨

汉明太强了！！！！！！！！真是妙蛙种子吃着妙脆角妙进了米奇妙妙屋妙到家了

---

一个数据，如何知道是分在那一组呢？

比如：第一组是1,3,5,7，为什么要这样子分，我们为什么知道是这个样子？
前面我们看到。如果我们采用汉明编码，在接收方，我们对每一组代码进行检测，都会得到一个检测位【1或0,1表示出错，0表示正常】，如果我们把检测位按照组号进行排序【降序】，就可以得到一个二进制编码。而这个二进制编码的值就是出错的位置。这是汉明码的重要特征，那么编码技术，就是核心。我们如何给他们分组，如何确定对应位置是要在哪一个组？这是汉明码能发挥作用的关键。

---

每一组数的位置的特征

第一组：1,3,5,7
第二组：2,3,6,7
第三组：4,5,6,7
第一组，如果所有的位置都转化为二进制数，最右边的那一位都是1
第二组，如果所有的位置都转化为二进制数，从右往左，第二位的值都是1
第三组：如果所有的位置都转化为二进制数，从右往左，第三位的值都是1
如果说，二进制编码，从右往左，第一位和第二位都是1，那么这个数就是被第一组和第二组所共有。
如果说，二进制编码，从右往左，第一位和第三位都是1，那么这个数就是被第一组和第三组所共有。

---

汉明码的组成

1.一个字符串，我们要传输的话，要加多少位校验位？
2.校验位应该加在哪里？【加在位置为2的n次方上面，第i组，放在2的i-1次方的位置】
3.检验码的取值，我们要根据等待校验的组的1的个数来确定，如组中1的个数为偶数个且采用偶校验，这时的校验码取值就为0.【以此类推】

---

添加的校验位位数

添加多少检测位，就是将字符串分为多少组。对每一组进行检测，会得到不同的检测结果。这些检测结果组成一个数值，或是指出哪个位置出错了，或是指出没有错误。
原来有n位子符，添加k位检测位，要指出是哪里错误了，这些状态一共有n+k个，还有一个是没有出错，所以这个结果至少需要指出n+k+1种状态。这些状态我们使用k位二进制数进行编码

---

各检测位检测的数值

实际应用

1.求0101按“偶校验”配置的汉明码

因为n=4，
且2^k>=n+k+1
所以k=3

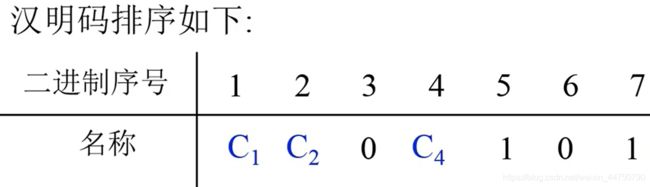
第一组：里面有1,3,5,7，因为位置3是0，位置5是1，位置7是1，又是偶校验，所以C1=0.
第二组：里面有2,3,6,7，因为位置3是0，位置6是0，位置7是1，又是偶校验，所以C2=1.
第三组：里面有4,5,6,7，因为里面1的个数为偶数个，所以我们C4=0.
所以编码是0100101

2.按配偶原则配置0011的汉明码

结果为1000011

3.汉明编码的纠错过程

已知接收到的编码为0100111（按照配偶原则），试问要传递的信息是什么？
解：此时

所以第二组和第三组的一个公共位置一起出错了【6,7】，那为什么不是7错了呢？如果7错了，那么第一组的结果也应该会是1，所以7不是错误的【这里只假设每次出错只会错一个字符】
此时 P4P2P1=110【二级制转化为十进制为6】，因此第六个位置出错了，改过来，所以要传递的信息是0101.

---

练习：

看到这里，应该对汉明编码的理解有了不同的认识了，如果上面有说错的地方，欢迎各位朋友指正【一起学习，一起进步】