测试函数shubert(十)自适应变异粒子群求解方法
测试函数shubert(十)
shubert函数属于周期性多峰函数,如图1所示拥有多个全局最优值,如图二所示在一个周期内只有一个全局最优值,局部最优解较多,适合测试算法的收敛性能,粒子群算法是一种收敛速度较快的算法,运算速度快,但是粒子群算法容易陷入局部最优,有些时候会导致收敛慢,或者不收敛,本文用标准粒子群算法进行改进,加入自适应变异,用自适应变异粒子群AMPSO求解,如有疑问,欢迎大家留言交流!
函数图像如下
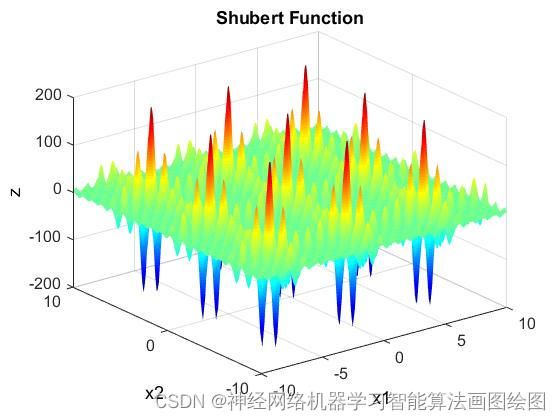
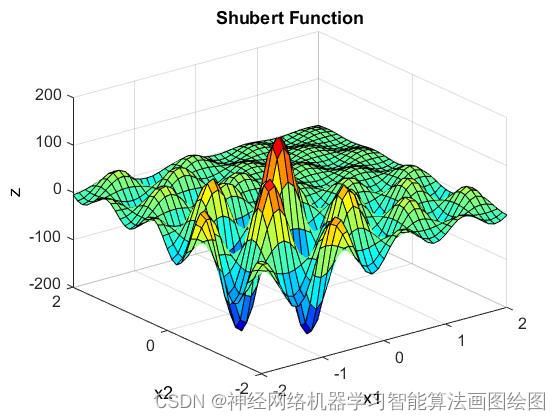
MATLAB编程shubert代码如下:
clc
clear
close all
x = -2:0.1:2;
y = -2:0.1:2;
x = -10:0.1:10;
y = -10:0.1:10;
[x,y] = meshgrid(x,y);
[m,n] = size(x);
z = zeros(m,n);
for ii = 1:m
for jj = 1:n
xx = [x(ii,jj) y(ii,jj)];
z(ii,jj) = shubertfun(xx);
end
end
figure
surf(x,y,z)
xlabel('x1')
ylabel('x2')
zlabel('z')
axis([-2 2 -2 2 -200 200])
% axis([-10 10 -10 10 -200 200])
% shading interp
title('Shubert Function')
set(gca,'fontsize',12)
colormap jet
function [ out] = shubertfun( x )
x1 = x(1);
x2 = x(2);
sum1 = 0;
sum2 = 0;
for ii = 1:5
new1 = ii * cos((ii+1)*x1+ii);
new2 = ii * cos((ii+1)*x2+ii);
sum1 = sum1 + new1;
sum2 = sum2 + new2;
end
out = sum1 * sum2;
end
自适应变异粒子群AMPSO算法的原理
粒子群优化算法(PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法,PSO是由Kennedy和Eberhart共同提出,最初用于模拟社会行为,作为鸟群中有机体运动的形式化表示。自然界中各种生物体均具有一定的群体行为,Kennedy和Eberhart的主要研究方向之一是探索自然界生物的群体行为,从而在计算机上构建其群体模型。PSO是一种启发式算法,因为它很少或没有对被优化的问题作出假设,并且能够对非常大候选解决方案空间进行搜索。PSO算法初始化为一群随机的粒子,然后通过多次迭代找到最优解。每一次的迭代过程中,粒子通过本身所找到的最优解(被成为个体极值)和整个种群目前找到的最优解(被称为全局极值)来更新自己。也可以使用粒子本身的邻居(被称为局部极值)的极值来更新自己,粒子群算法收敛快,但是容易陷入局部最优,针对次问题,本文增加一个判断是否陷入早熟的参数p,当粒子群种群的适应度值区域一致,既粒子群的适应度值均方误差小于参数p的时候,判断粒子群太过聚集,陷入早熟,对种群就行自适应变异,打散种群,从新全局搜索。
AMPSO粒子群算法的主要参数
一、种群个数popsize,既算法中粒子的个数;
二、最大迭代次数gen,既算法迭代gen次后停止迭代;
三、种群维度dim,既需要优化的自变量个数;
四、种群位置pop,既每个粒子群的对应的自变量的值,一个粒子对应一组自变量,相当于一个解;
五、种群速度v,既粒子群每次迭代更新的飞行速度,粒子群位置更新的步长;
六、种群全局最优值gbest,既迭代过程中曾经出现的最优解,包括最优位置和对应的目标函数值;
七、个体最优,既每个粒子迭代过程中单个体曾经出现的个体最优解,,包括个体最优位置和对应的目标函数值;
八、个体学习因子c1,既个体最优解对粒子群飞行的影响能力;
九、全局学习因子c2,既全局最优值对粒子群飞行的影响能力;
十、惯性权重w,既个体位置所占的权重,权重越大,粒子群收敛越慢,全局搜索能力越强;
十一、阈值p,判断粒子群聚集程度的参数,适应度值均方误差小于参数p的时候,判断粒子群太过聚集,陷入早熟。
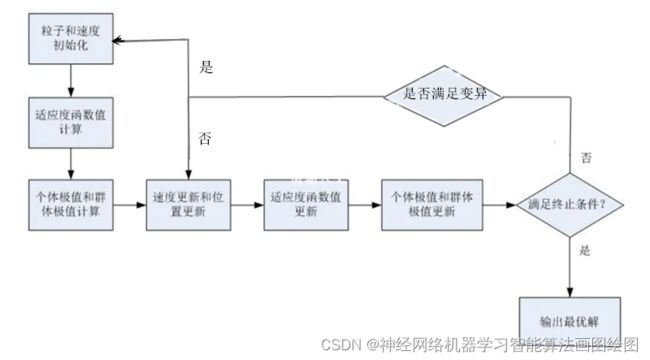
自适应变异粒子群算法流程图
自适应变异粒子群AMPSO的MATALB编程代码如下:
clc
clear
close all
warning off
set(0,'defaultfigurecolor','w')
%x y
xmax = [5.12 5.12];
xmin = [-5.12 -5.12];
vmax = 0.2*xmax;
vmin = -vmax;
fun = @shubert;
m=2;
%程序初始化
% global popsize; %种群规模
gen=20; %设置进化代数
popsize=300; %设置种群规模大小
best_in_history(gen)=inf; %初始化全局历史最优解
best_in_history(:)=inf; %初始化全局历史最优解
best_fitness=inf;
fz = zeros(gen,5);
%设置种群数量
pop1 = zeros(popsize,m);
pop2 = zeros(popsize,m);
pop3 = zeros(popsize,m);
pop6 = zeros(gen,m);%存储解码后的每代最优粒子
pop7 = zeros(popsize,m);%存储更新解码后的粒子的位置
for ii1=1:popsize
pop1(ii1,:)=funx(xmin,xmax,m); %初始化种群中的粒子位置,
pop3(ii1,:)=pop1(ii1,:); %初始状态下个体最优值等于初始位置
pop2(ii1,:)=funv(vmax,m); %初始化种群微粒速度,
pop4(ii1,1)=inf;
pop5(ii1,1)=inf;
end
pop0=pop1;
xmax = [5.12 5.12];
xmin = [-5.12 -5.12];
c1=2;
c2=2;
gbest_x=pop1(end,:);
% pop1(1:size(num,1),:) = num; %全局最优初始值为种群第一个粒子的位置
for exetime=1:gen
reset =1; % reset = 1时设置为粒子群过分收敛时将其打散,如果=1则不打散
if reset==1
bit = 1;
for k=1:popsize
bit = bit&(range(pop1(k,:))<0.2);
end
if bit==1 % bit=1时对粒子位置及速度进行随机重置
for ik = 1:popsize
pop1(ik,:) = funx(xmin,xmax,m); % present 当前位置,随机初始化
pop2(ik,:) = [0.02*rand()-0.01 0.02*rand()-0.01]; % 速度初始化
end
for k=1:popsize % 重新计算适应度
pop5(k,1) =fun2(pop1(k,:));
end
warning('粒子过分集中!重新初始化……'); % 给出信息
display(exetime);
end
end
ww = 0.7*(gen-exetime)/gen+0.2;
for ii4=1:popsize
pop2(ii4,:)=(ww*pop2(ii4,:)+c1*rand(1,m).*(pop3(ii4,:)-pop1(ii4,:))+c2*rand(1,m).*(gbest_x-pop1(ii4,:))); %更新速度
for jj = 1:m
if pop2(ii4,jj)vmax(jj)
pop2(ii4,jj)=vmax(jj);
end
end
end
%更新粒子位置
for ii5=1:popsize
pop1(ii5,:)=pop1(ii5,:)+pop2(ii5,:);
for jj2 = 1:m
if pop1(ii5,jj2)>xmax(jj2)
pop1(ii5,jj2) = xmax(jj2);
elseif pop1(ii5,jj2)0.85
% k=ceil(m*rand);
% pop1(ii5,k) = (xmax( k)-xmin(k)).*rand(1,1)+xmin(k);
% end
% if pop5(ii5)>sum(pop5)/popsize
% pop1(ii5,:) = (xmax(1,m)-xmin(1,m)).*rand(1,m)+xmin(1,m);
% end
end
for jj2 = 1:m
if pop1(ii5,jj2)>xmax(jj2)
pop1(ii5,jj2) = xmax(jj2);
elseif pop1(ii5,jj2)0
plot(1:length(best_in_history(1:exetime-1)),best_in_history(1:exetime-1));
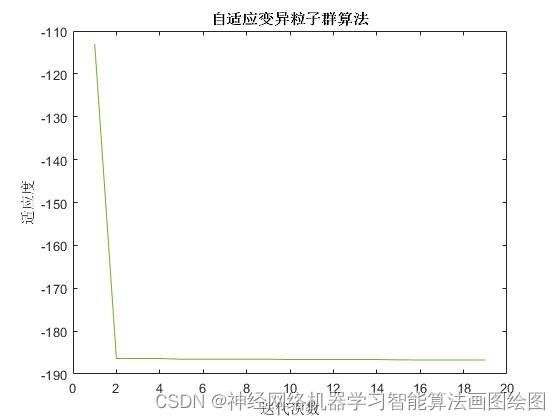
xlabel('迭代次数')
ylabel('适应度')
title('粒子群算法')
hold on;
pause(0.1)
end
pop1(end,:) = gbest_x;
%计算适应值并赋值
for ii3=1:popsize
[my,mx] = fun2(pop1(ii3,:));
% [my,mx] = fun2(gbest_x,num,xmax,xmin);
pop5(ii3,1)=my;
pop7(ii3,:) = mx;
if pop4(ii3,1)>pop5(ii3,1) %若当前适应值优于个体最优值,则进行个体最优信息的更新
pop4(ii3,1)=pop5(ii3,1); %适值更新
pop3(ii3,:)=pop1(ii3,:); %位置坐标更新
end
end
%计算完适应值后寻找当前全局最优位置并记录其坐标
if best_fitness>min(pop4(:,1))
best_fitness=min(pop4(:,1)) ; %全局最优值
ag = [];
ag =find(pop4(:,1)==min(pop4(:,1)));
gbest_x(1,:)=(pop1(ag(1),:)); %全局最优粒子的位置
pop6(exetime,:) = pop7(ag(1),:);
else
fz(exetime,:) = fz(exetime-1,:);
if exetime>1
pop6(exetime,:) = pop6(exetime-1,:);
end
end
best_in_history(exetime)=best_fitness; %记录当前全局最优
end
x = -2:0.1:2;
y = -2:0.1:2;
x = -10:0.1:10;
y = -10:0.1:10;
[x,y] = meshgrid(x,y);
[m,n] = size(x);
z = zeros(m,n);
for ii = 1:m
for jj = 1:n
xx = [x(ii,jj) y(ii,jj)];
z(ii,jj) = shubertfun(xx);
end
end
figure
surf(x,y,z)
hold on
xlabel('x1')
ylabel('x2')
zlabel('z')
axis([-2 2 -2 2 -200 200])
% axis([-10 10 -10 10 -200 200])
% shading interp
title('Shubert Function')
set(gca,'fontsize',12)
colormap jet
plot(pop0(:,1),pop0(:,2),'ro','MarkerFaceColor','r')
xlabel('X')
ylabel('Y')
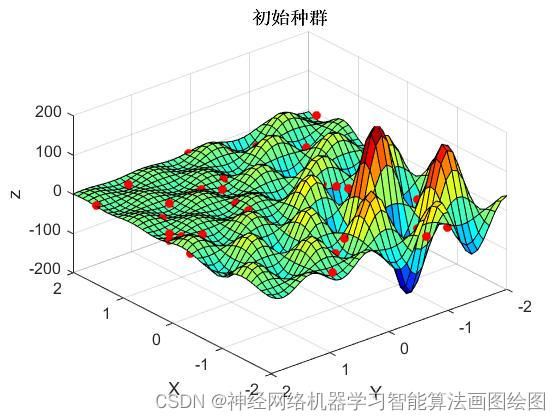
title('初始种群')
set(gca,'fontsize',12)
view([-130 40])
figure
surf(x,y,z)
hold on
xlabel('x1')
ylabel('x2')
zlabel('z')
axis([-2 2 -2 2 -200 200])
% axis([-10 10 -10 10 -200 200])
% shading interp
title('Shubert Function')
set(gca,'fontsize',12)
colormap jet
plot(pop1(:,1),pop1(:,2),'ro','MarkerFaceColor','r')
xlabel('X')
ylabel('Y')
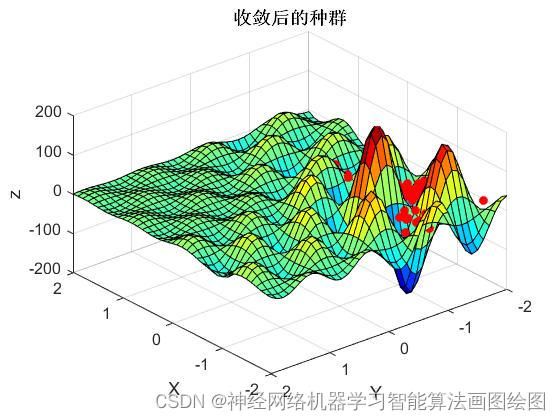
title('收敛后的种群')
set(gca,'fontsize',12)
view([-130 40])
function [out,xy]= fun2(xy)
xmax = [5.12 5.12 ];
xmin = [-5.12 -5.12 ];
for ii = 1:2
if xy(ii)>xmax(ii)
xy(ii)=xmax(ii);
elseif xy(ii)