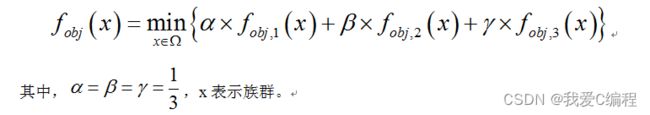m云计算任务调度优化matlab仿真,输出成本,时间,负荷优化结果,对比ACO,PSO,WOA三种优化算法
目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
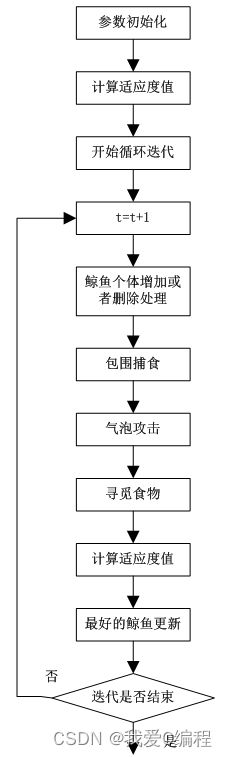
1.算法描述
鲸鱼算法(Whale Optimization Algorithm,WOA)[1]。鲸鱼优化算法(WOA)是 2016 年由澳大利亚格里菲斯大学的 Mirjalili 等提出的一种新的群体智能优化算法,因算法简练易于实现,且对目标函数条件要求宽松,参数控制较少等种种优点受到一批又一批学者的亲睐,且经过不断的改进WOA已应用于许多领域。WOA算法设计的既精妙又富有特色,它源于对自然界中座头鲸群体狩猎行为的模拟, 通过鲸鱼群体搜索、包围、追捕和攻击猎物等过程实现优时化搜索的目的。在原始的WOA中,提供了包围猎物,螺旋气泡、寻找猎物的数学模型。
WOA算法的初始阶段中,座头鲸并不知道食物所在的位置,他们都是通过群体合作来获得食物的位置信息,因此,距离食物最近的鲸鱼相当于当前的一个局部最优解,其他鲸鱼个体都会朝这个位置靠近,从而逐步包围食物,因此使用下列的数学模型表示:
2.2气泡攻击
本阶段模仿座头鲸进行气泡攻击,通过收缩包围和螺旋更新位置来设计鲸鱼捕食吐出气泡的行为,从而达到鲸鱼局部寻优的目的。
(1)螺旋更新位置
座头鲸个体首先计算与当前最优鲸鱼的距离,然后再以螺旋方式游走,在进行食物的搜索时候,螺旋游走方式的数学模型为:
2.3寻觅食物阶段
座头鲸通过控制|A|向量游走获取食物,当|A|>1的时候,座头鲸个体向着参考座头鲸的位置靠近,鲸鱼个体朝着随机选取的座头鲸更新位置,这种方式保证了座头鲸个体能够进行全局搜索,获得全局最优解,其数学模型表示如下:
优化目标函数概述:
优化目标函数做如下的设计:
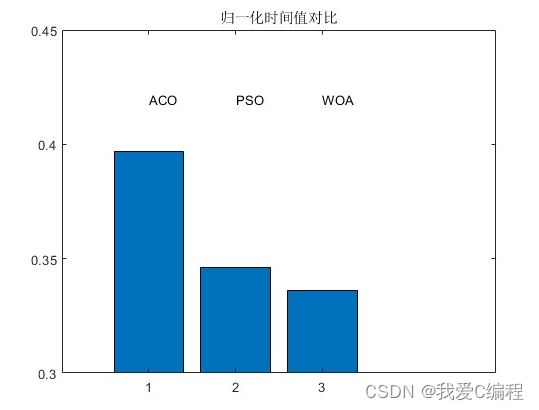
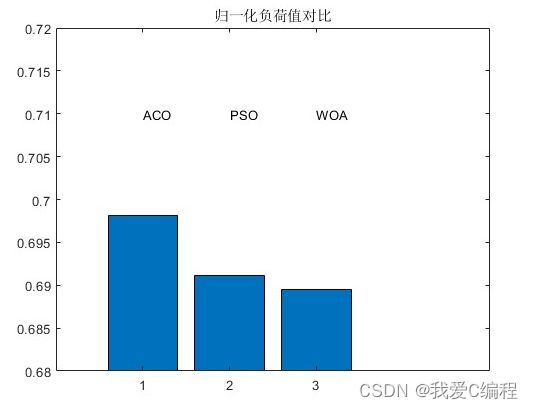
即成本,时间,负荷
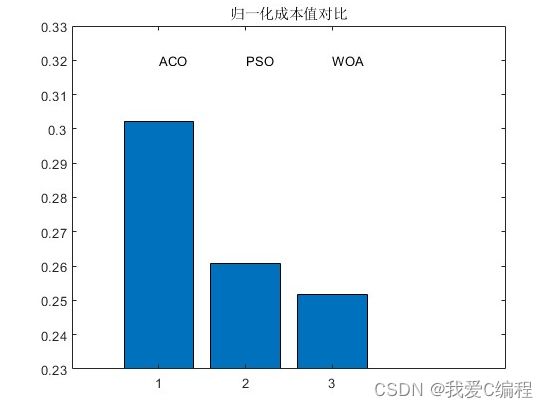
2.仿真效果预览
matlab2022a仿真如下:
3.MATLAB核心程序
Num = 50; %搜索数量
Iters = 200; %迭代次数
D = M*N; %搜索空间维数
woa_idx = zeros(1,D);
woa_get = inf;
%初始化种群的个体
for i=1:Num
for j=1:D
xwoa(i,j)=randn; %随机初始化位置
end
end
for t=1:Iters
t
for i=1:Num
%目标函数更新
[pa(i),pa1(i),pa2(i),pa3(i)] = fitness(xwoa(i,:));
Fitout = pa(i);
%更新
if Fitout < woa_get
woa_get = Fitout;
woa_idx = xwoa(i,:);
end
end
%调整参数
c1 = 2-t*((1)/300);
c2 =-1+t*((-1)/300);
%位置更新
for i=1:Num
r1 = rand();
r2 = rand();
K1 = 2*c1*r1-c1;
K2 = 2*r2;
l =(c2-1)*rand + 1;
rand_flag = rand();
for j=1:D
if rand_flag<0.5
if abs(K1)>=1
RLidx = floor(Num*rand()+1);
X_rand = xwoa(RLidx, :);
D_X_rand = abs(K2*X_rand(j)-xwoa(i,j));
xwoa(i,j)= X_rand(j)-K1*D_X_rand;
else
D_Leader = abs(K2*woa_idx(j)-xwoa(i,j));
xwoa(i,j)= woa_idx(j)-K1*D_Leader;
end
else
distLeader = abs(woa_idx(j)-xwoa(i,j));
xwoa(i,j) = distLeader*exp(6*l).*cos(l.*2*pi)+woa_idx(j);
end
end
end
[pb,pb1,pb2,pb3] = fitness(woa_idx);
Pbest(t) = pb;
Pbest1(t) = pb1;
Pbest2(t) = pb2;
Pbest3(t) = pb3;
end
figure;
subplot(221);
plot(Pbest,'b');
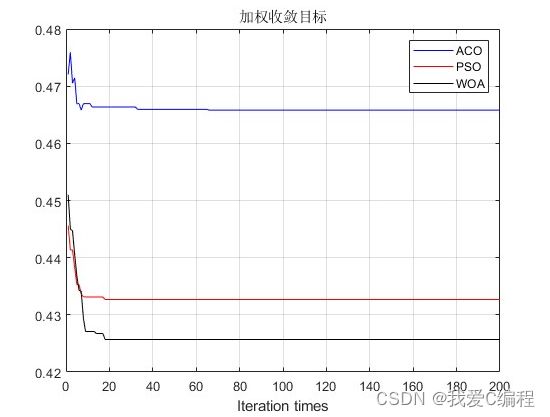
legend('加权收敛目标');
grid on
%输出三个指标的收敛曲线
subplot(222);
plot(Pbest1,'b');
legend('归一化成本值');
grid on
subplot(223);
plot(Pbest2,'b');
legend('归一化时间值');
grid on
subplot(224);
plot(Pbest3,'b');
legend('归一化负荷值');
grid on
%输出调度结果
[aij,fobj,fobj1,fobj2,fobj3] = fitness_results(woa_idx);
%显示各个资源的三个指标的利用率
%处理能力利用率
for i = 1:M
tmps = aij(:,i);
indx = find(tmps==1);
SE(i)= sum(Et(indx))/En(i);
end
%内存利用率
for i = 1:M
tmps = aij(:,i);
indx = find(tmps==1);
SS(i)= sum(St(indx))/Sn(i);
end
%带宽利用率
for i = 1:M
tmps = aij(:,i);
indx = find(tmps==1);
SC(i)= sum(Ct(indx))/Cn(i);
end
02_056m4.完整MATLAB
V