OM | 运筹学在医疗运营管理中的应用

作者：沈一华（清华大学） 茹伟明（香港理工大学）

本文基于Abdur Rais和Ana Viana 在International Transactions in Operational Research期刊中发表的论文“Operations Research in Healthcare: a survey” 介绍了医疗运营管理中的不同应用场景，并探讨了常见的运筹学解决方案。

随着众多发达国家出生率的下降和全球平均寿命的增加，医疗中的优化问题正得到运筹学界越来越多的关注。多年来，人们的关注重点从资源分配和战略规划问题逐渐扩展至包括资源调度和治疗规划等在内的运营管理问题。这篇文章将综述运筹学在医疗领域的主要应用，特别是现行的优化问题及其解法在这一领域的主要贡献。

一 背景

如何确定医疗诊所和救护车的最佳位置来最大化针对特定群体的医疗覆盖面积？如果车辆到达医院的总距离需小于特定数值，需要多少个医疗救护车基地? 如何规划放射性治疗以最小化癌症病人的治疗时间？如何安排创伤中心护士们的工作时间以确保即使在最坏情况下依然能维持足够的服务水平？医疗中有许多类似的问题亟待处理，而运筹学能为此提供解决之道。

虽然医疗场景下的优化问题在过去几十年中就已经得到了相当程度的关注，但由于众发达国家出生率下降导致的人口老龄化趋势和全球平均寿命的增加，许多问题现在变得更加重要且影响深远；此外，数目庞大的公共和私人资金需要用以支付迅速上升的医疗保健费用，这也需要对节约成本的措施进行更仔细地审查。例如，美国花费超过2万亿美元或其GDP的16%用于医疗保健，尽管如此依然有5000万美国人没有医疗保险，另有2500万人仍然保险不足。毫无疑问，医疗问题是目前美国最主要的社会和经济问题之一。

如今，人们已经在研究中发现了许多新的优化问题和解决方案。我们重点关注的医疗优化问题，包括服务规划、资源调度、物流、医学疗法、疾病诊断和预防性护理等。

二 医疗规划

在提供适当和充足的医疗服务仍然是大多数国家关注的一个重要问题的今天，医疗规划的重要性怎么强调都不为过。在人口出生率不断下降的情况下，由于平均寿命的增加和人口老龄化趋势的发展，许多国家正越来越难以获得额外的预算和资源来满足医疗保健的需求。许多国家正将目光投向运筹学，以寻找优化和成本控制措施。这其中的关键问题包括需求预测、医院选址、紧急设施设计等。仿真模拟是一个强大的规划工具，而其他许多技术也在这些方面发挥了重要作用。

2.1 需求预测

一个领先的医疗保健系统花费数千万美元建造了一个大型心血管中心，以期心脏直视手术的持续增长能产生可观的利润。然而，心内直视手术率的快速、史无前例的下降，对财务预测更加不利。社区医院在扩大急诊科上投入巨资，但由于没有考虑到更有效的病人吞吐量、增加危重症护理床位和建立急诊观察室对病人数量的影响，因此产能过剩。如果卫生系统和医院能够更好地预测治疗模式的变化将如何影响未来的服务需求，上述两种情况都是可以避免的。对医院服务的需求可能会发生意想不到的变化，而需求预测可以为这些变化做好准备，避免战略失误。

精准的需求预测在医疗规划中十分重要，因为它的结果将成为许多优化问题的输入。预测方法可分为定性和定量两种，而大多数研究都因更好的准确性而更多关注定量方法。然而，准确的历史数据的可获得性对于量化方法来说非常关键。

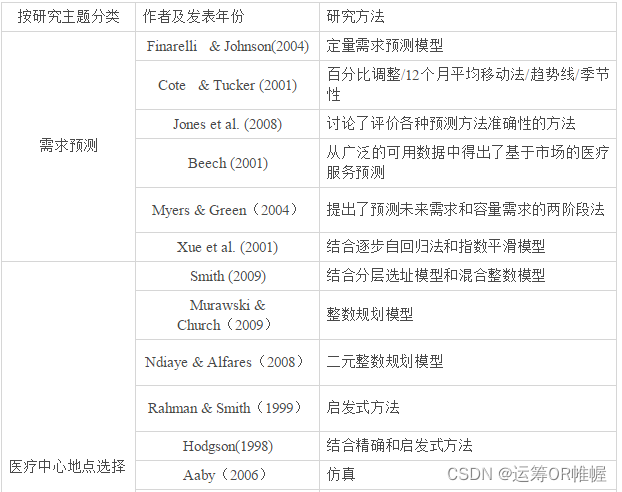
Finarelli和Johnson(2004) 提出了详细的九步骤定量需求预测模型，而Cote和Tucker (2001)讨论了四种常见的需求预测方法，包括百分比调整(percent adjustment), 12个月平均移动法(12-month moving average),趋势线 (trendline)和季节性 (seasonality). Jones等 (2008)讨论了评价各种预测方法准确性的方法，他们的论文运用了三家不同医院中每天病人到达急诊科的数据，并使用了时间序列分析、指数光滑、季节自回归综合移动平均和人工神经网络模型等方法。

Beech (2001)从广泛的可用数据中得出了基于市场的医疗服务预测，以估计未来的需求。数据集涉及初级和二级服务领域、不同人口分组下的各服务区人口、排放利用率、市场规模和市场份额。他们发现，市场动态可以引发各种对潜在未来需求情景的假设。

Myers和Green（2004）提出了预测未来需求和容量需求的两阶段法。特别地，他们的方法能制定一项设施总计划，既考虑了设施容量，也考虑医生的要求。

Xue等人（2001）分析了美国终末期肾病人口的持续增长现象。他们针对历史数据运用逐步自回归法和指数平滑模型预测了直到2010年的数据。

2.2 地点选择

在医疗领域，选址不当的影响远远超出了基于成本和客户服务方面的考虑。如果可利用的设施太少或设施的选址不好，就会导致死亡率和发病率的提高。有大量的研究关注医疗中的容量管理和设施选址问题，这既涉及医疗服务，也针对医疗材料。

2.2.1 医疗中心

运筹学实践者们广泛研究了如何确定医疗中心的位置以最大化可到达性这一问题。Smith (2009)等关注在发展中国家的乡村地区设计可持续社区卫生保健规划这一问题。他们同时考虑了自上而下和自下而上的分层选址模型，以有效规划社区卫生计划，并提出了一个混合整数模型来确定可持续设施的位置。

Murawski和Church（2009）研究了通过将交通网络现有设施点的连接升级到全天候道路来提升医疗服务可达性的问题。他们的整数规划模型适用于发展中国家的农村地区，在恶劣天气状况下那里由于缺乏全天候道路，医疗设施的可达性时常会大大降低。他们的模型在加纳得到了很好的应用。

Ndiaye和Alfares（2008）研究了一个略有不同的问题。他们关注为在不同季节会改变其居住地点的游牧人口群体选择公共服务地点的问题。他们提出了一个二元整数规划模型来确定能满足季节变化需求的最佳的医疗中心数量和位置。

Rahman和Smith（1999）讨论了为农村地区的医疗设施寻找更多的合适的建设地点的问题，并将该问题建模为最大覆盖位置模型。他们针对孟加拉国的数据运用启发式方法解决了这一问题。

最后，Hodgson(1998)等运用covering tour model规划流动保健服务，使足够数量的设施在地理位置分布上既可到达，也可持续。他们的整数线性规划模型使得一定区域内的人到流动设施的距离最小。他们同时运用了精确和启发式方法来解决这一问题，并利用来自加纳的历史数据给出数值结果。

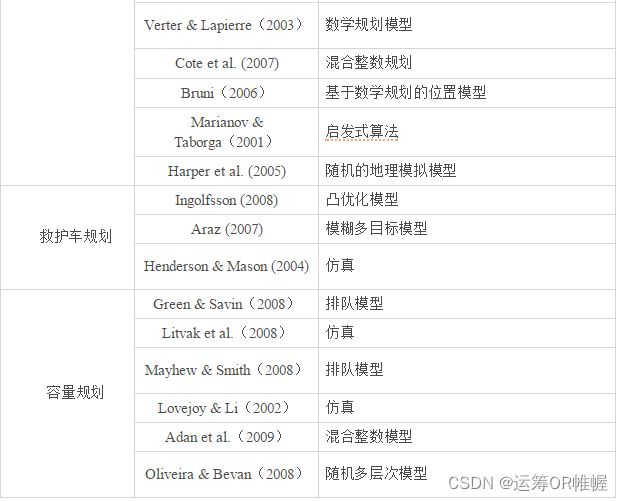
Aaby（2006）等讨论了另一些设施选址问题。他们设计了一种仿真工具以规划爆发性流感中大规模接种诊所的地点。Verter和Lapierre在2003年也研究了预防性保健设施的选址问题。他们提出了一个数学规划模型使得参与这项预防性项目的人数最大化，并用来自美国佐治亚和加拿大蒙特利尔的数据演示了结果。

Cote等人（2007）关注现役军人的创伤性脑损伤问题。由于及时的治疗对于康复十分关键，我们希望病人能离拥有专业化设施的康复中心越近越好。他们提出了一个混合整数规划模型以规划新诊所的位置，同时尽量减少病人的费用（治疗、住宿、旅行），和与放弃治疗、设施过剩等问题相关的惩罚性费用。

意大利移植系统的组织结构是Bruni（2006）等人工作的重点。他们提出了一个基于数学规划的位置模型来优化这样的组织结构。特别地，他们考虑了时间在移植过程中的关键作用和移植中心的空间分布。该模型的目的是跨区域分配移植器官，实现医疗保健方面的区域公平性。

Marianov和Taborga（2001）关注公共保健中心的地理位置规划问题，其目标是在预先规定的距离内最大限度地覆盖低收入人口。Harper等人（2005）在服务的地理位置及需要服务的病人都十分重要的情况下，分析了有关服务规划的问题。他们提出了一个随机的地理模拟模型来展现患者前往各医院的动态过程，同时考虑到必要的资源容量、患者需求的可变性和他们路途中的其他因素。

2.2.2 紧急车辆

救护车规划问题包括救护车地点和运行时间部署等战略决策和调度策略选择等运营决策。任何解决方案都需要在政治、经济和医疗目标之间小心平衡。定量决策过程在为必须做出的资源决策承担公共责任方面变得越来越重要。

Ingolfsson (2008) 等提出了一个救护车设施选址模型以最小化为执行预先指定的服务水平而需要的服务单位矢量。他们将不确定性和随机性融入了他们的凸优化模型，并用加拿大埃德蒙顿的实际数据进行分析。他们发现，这一模型可成为针对多达一百万人口的城市的通用优化分析器。

Araz (2007) 研究为优化服务水平而确定在数量有限的紧急车辆情形下的最佳基地选址问题。他们采用了三个指标来衡量服务水平，分别是一辆车的最大覆盖人口数、所有后备车辆的最大人口覆盖数和从超出特定距离的位置到服务店的距离最小化这三方面。他们运用了一个模糊多目标模型来解决这一问题。

Henderson和Mason (2004) 研究运用仿真和分析软件来解决救护车服务规划问题。决策支持系统有各种先进的功能可用于战略和实际等不同层面下的运营管理。目前，它帮助澳大利亚、新西兰和美国的几个组织提供了高效的救护车服务。

2.3 容量规划

为及时地为病人提供护理，无论是在同一天还是在几天内，都需要一定的最小医疗资源供给来匹配病人的需求。

医院的容量规划对运筹学从业者来说充满了具有挑战性的问题。例如，Green和Savin（2008）使用基于OR的分析来解决日益危急的医院容量规划问题。他们运用了排队模型，并分析了如何从OR模型中得出对运营管理具有重要意义的战略措施。

Litvak等人（2008）提出了针对荷兰医院治疗急诊病人如何分配病房的合作性解法。他受到电信通信中电话流的启发提出了一种数学方法，并用仿真模型验证了结果。Mayhew和Smith（2008）也对应急部门进行了研究。他们使用排队模型来评估英国医院的急诊科。根据政府规定的目标，他们专注于如何在4小时内使病人在医院内完成医疗流程并顺利出院。最后，Lovejoy and Li（2002）研究医院是应当通过建造更多的手术室，还是延长当前手术室的工作时间来满足容量需求。他们提出了一种多目标模型来实现以下三个目标：最小化等待按期接受治疗的病人数、最大化治疗开始时间的稳定性、最大化医院的利润。他们对各目标进行权衡，并用仿真工具验证了模型。

在战术层面上，Adan等（2009）关注心胸外科中心为优化资源使用而面临的问题。他们将其建模为具有随机停留时间的混合整数模型，其研究结果表明，为了实现既定的病人吞吐量目标，我们可以通过考虑确定性问题的随机性方面来设计能够更好利用资源的手术时间表。

Oliveira和Bevan（2008）估计了每单位产出中随之产生的不可避免的医疗费用和低效性。他们研究出一种随机多层次模型并将其应用于葡萄牙的医院。他们强调了床位分配、奖励和规模经济中产生的各种效率低下的问题。他们的模型可以捕捉不同种类医院中的成本变化。

表1. 医疗规划相关文献及其研究方法分类

 三 医疗管理和物流

医疗保健中的病人调度、资源调度和物流问题可能是传统OR期刊中最广泛引用的管理问题，特别是护士日程的安排问题。

3.1 患者调度

一个优化的患者-工作人员/患者-设施排程表可以显著减少费用，提高服务质量。

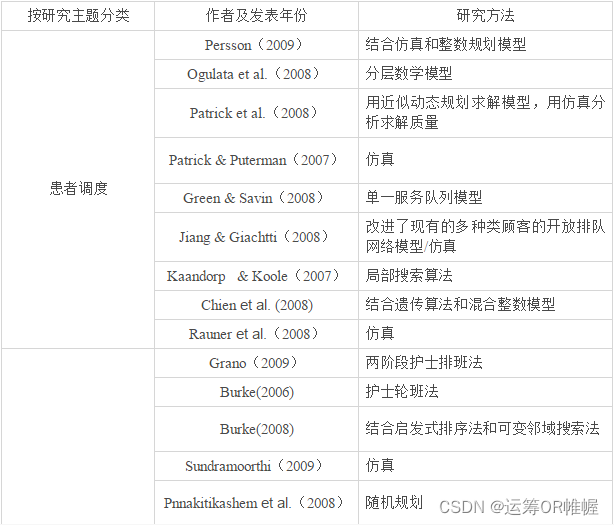
Persson（2009）关注在医疗、经济和时间等因素限制下，瑞典一家医院的患者排程问题。根据瑞典的政策，为防止排长队，病人可以被分配至其他医院接受手术。他们设计了一种混合仿真和整数规划模型来解决这一问题。

Ogulata等（2008）研究了患者-工作人员的调度。他们建立了分层数学模型来生成时间表，并考虑了三个子问题：（1）病人的选择；（2）如何分配病人给工作人员；（3）如何在一天之中分配病人不同的治疗时间。他们的目标是最大限度地增加选定的病人人数，以平衡治疗工作量并尽量减少患者在治疗日的等待时间。他们用医院的真实数据测试了他们的模型。

Patrick等（2008）用马尔科夫决策过程建模，描述了将具有不同优先级的病人动态分配至公共健康中心的过程。他们用近似动态规划求解模型，并用仿真分析其求解质量。Patrick和Puterman（2007）也用仿真技术来安排灵活的住院时间表，以提高诊疗过程中服务资源的利用率。

Green和Savin（2008）分析了病人最后一分钟取消预约的问题，并将其建模为一个单一服务队列问题。他们推导出了队列大小的平稳分布，并给出了丰富的计算结果以及对未来相关研究的建议。

在另一系列的研究中，Jiang和Giachtti（2008）讨论了门诊设施中的病人流动问题，并考虑了减少一定时间内的并行活动。他们改进了现有的多种类顾客的开放排队网络模型，并证明并行化确实可以减少需要多种诊断或治疗程序的患者的周期性时间。他们将结果与仿真结果进行了比较。Kaandorp和Koole（2007）考虑了门诊预约的时间安排，并提出一个局部搜索算法。这一算法在目标是患者预期等待时间、医生空闲时间和迟到时间的加权平均数时收敛到最优结果。他们发现，针对特定组合的参数，Bailey-Welch规则能给出一个最优的预约时间计划。

Chien(2008)等人使用遗传算法，通过减少病人等候时间、增加治疗设备来安排病人治疗流程、提高服务质量。该问题被建模为混合车间调度问题。他们使用混合整数模型作为验证解决方案质量的基准，并使用台湾某医疗中心的数据来验证该方法。

Rauner等人（2008）设计了一个基于离散事件仿真的网络游戏，以描述医院的经济和组织决策过程。多达6家医院的管理层可以为各种疾病类别和预算的患者提供服务；玩家可以通过对资源、流程和财务状况的分析进行容量管理和病人排程。

3.2 资源调度

资源调度一直是医疗保健研究中的一个活跃领域——人们始终希望能不断提高容量利用率、控制成本，并提高服务的运营效率。

3.2.1 护士调度

医院需要提供24小时的各级护理服务，以满足病人的需求；同时遵守旨在保护病人和工作人员健康和福利的组织政策。护士的短缺使本来就很困难的日程安排问题更加复杂化，因此护士的留存是大多数医疗机构非常关心的问题。护理人员的高流动率是工作不满意的结果，而不灵活的工作安排是导致不满意的一个重要原因。许多医院建立了自主排班制度，旨在为护士们提供更多灵活性并提高工作满意度。总体而言，护士排班问题关注如何将轮班分配给具有不同技能的护士，同时满足尽可能多的软约束和个人偏好。护士时间表通常希望在预定的规划期间满足所需的人员覆盖范围。

在最近的一篇论文中，Grano（2009）提出了一个两阶段护士排班方法，同时考虑到了护士的偏好和医院的需求。这一优化模型首先在满足医院的所有约束的情况下将班次排给“出价”最高的护士，随后的优化过程再逐渐将剩余的轮班安排给其他护士以完成时间表。他们将这一方法应用到美国宾夕法尼亚州一家医院急诊科的案例中。Burke(2006)也分析了这一问题，他们提出了一种基于现实世界的护士轮班方法，比传统的基于固定周期的方法更加灵活。此外，Burke(2008)将启发式排序法与可变邻域搜索相结合，而Sundramoorthi（2009）提出了仿真方法来评估护士-病人的安排。他们用德克萨斯州一家医院的真实数据集来验证他们的结果。

在某些情况下，病人可能需要被分配给具有特殊技能的特定护士。Pnnakitikashem等（2008）给出了这种情况下分配护士的随机规划方法。Mullinax和Lawley（2002）给出了为重病的新生儿分配护士的数学规划和启发式方法。

一个值得特别注意的问题是护士的重新排班问题。当至少有一名护士宣布她将无法承担以前分配给她的任务时，我们就会遇到这种情况。Pato and Moz（2008）利用遗传算法解决了这一问题，而Moz和Pato（2005）则将其作为一个双目标问题，并利用目标规划来解决它。

Steeg和Schroder（2007）关注如何尽量减少探视某个病人的护士人数（也称为“护士-病人忠诚度”）这一问题。他们提出了一个混合式方法，将约束规划和大邻域搜索的启发式方法相结合。在类似的研究中，Bertels和Fahle（2006）考虑了家庭保健问题，即在家中探视和护理病人。除了寻找最优护士的时间表外，他们还考虑了相关的路由问题：每个护士必须能够通过公共交通访问给定名册中的病人，其目标是尽量减少交通成本，并最大限度地提高病人和护士的满意度。线性规划、约束规划和元启发方法都被用来解决这一问题。

Bard和Purnomo（2005）研究了在硬约束和软约束下的护士偏好调度问题，并使用启发式与整数规划相结合的方法解决了这一问题。他们延伸了自己此前的工作，并通过加入降级选项，提高了时间安排的质量。此外，他们还提出了将循环调度和偏好调度相结合的方法，用整数规划建模并用拉格朗日松弛法求解。

3.2.2 手术室和医生排班

医院的管理人员通常会把注意力集中在手术室的工作时间安排上，因为满载的手术室带来的开销在预算中占很大比例，而且由于手术室的占用会带来对植入物等昂贵物品的需求，所以当医院管理者决定增加或减少手术室预算时，需要考虑哪些手术组将被分配以更多或更少的时间。Blake和Donald(2002)讨论了手术室排程问题，他们的模型可以用于决定每个外科医生应当被分配多少手术时间，尽管在多数情况下无法决定关于这些任务进行时间的详细时间。类似地，基于部分分支定界法的启发式算法被用于急诊室医生的排班以最小化与“偏差”约束相关的惩罚之和。

Ozkarahan (2000)讨论了另一系列优化目标，他提出了一种目标规划方法，在最小化手术室空闲时间和加班时间的同时最大限度地提高外科医生、病人和工作人员的满意度。Lamiri等人（2008）提出了一个随机模型用于择期手术和急诊手术这两种不同需求下的手术室规划。择期手术可以提前计划，并会因为手术日期的不同而产生与病人相关的费用；急诊手术以随机的方式到达，并必须在到达当天进行。这一规划问题需要我们将择期手术分配到一定规划周期内的不同时间区间中，以最小化与病人相关的择期费用和手术室的加班费之和。他们提出了一种将蒙特卡罗模拟与混合整数规划相结合的方法。

Santibanez（2007）等人设计了一个整数规划模型，通过考虑手术室时间的可用性和手术后资源的限制，将每个专科的手术安排到手术室中。不列颠哥伦比亚省卫生局的医院已经使用了这一模式。Zhang (2009a)等人通过整数规划和仿真模拟，每周将手术室的空闲时间分配给不同专科以最小化病人的住院费用（用他们在医院中停留的时间衡量）。

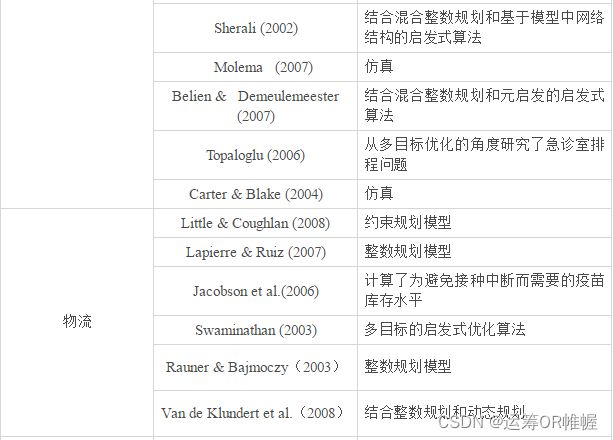
Pham和Klinkert(2008)提出了一种通过扩展作业车间调度问题的新方法来解决手术病例调度，而Green（2004）根据病人到达速率研究了调整急症室中工作人员数量以优化对病人的即时关照的问题。他通过评估各排队模型的有效性来探究能减少未被治疗就离开医疗系统的病人的比例的人员配置模式。Hans (2008)关注在最小化员工加班风险、确保没有手术取消、提升手术室利用率情形下的优化排程问题，并提出了一些具有建设性的局部搜索的启发式方法。居民随叫随到的日程安排涉及到部门人员配置需求、技能要求和居民偏好等问题，Wang (2007)等人使用遗传算法进行研究，而Sherali (2002)等人将其建模为一个混合整数规划问题，并通过基于模型中的网络结构的启发式算法来解决这一问题。

Molema (2007)分析了医生的兼职工作选择，他们通过针对两个案例的仿真发现兼职工作事实上可以提高服务质量和系统设计。Belien和Demeulemeester (2007)关注床位利用率，他们讨论了使床位使用率恒定的制定手术时间表的问题，并考虑两种约束：需求限制，以确保每个手术小组能够获得一定数量的手术室区块；容量约束，以限制每天可用的区块数量。他们研究了基于混合整数规划和元启发的启发式算法来最小化预期床位短缺。

急诊室排程问题受到许多规则的限制：对连续工作时间的限制、对每个住院医师应功过的日班和夜班数量的限制、根据日班和夜班工作人员年龄资质级别提出的要求、对连续安排的日班和夜班数量的限制、休假时间、周末休息时间的限制以及各员工间责任分配的公平性的问题。由于其中一些规则实际是内在冲突的，Topaloglu (2006)从多目标优化的角度研究了这一问题。

最后，Carter和Blake (2004)讨论了仿真工具能够发挥重要作用的四类问题，分别是住院手术调度、急诊室等待时间、急诊室调度和药品订购。他们讨论了使用仿真工具建模技术中的挑战和经验。

3.3 物流

医疗中的物流问题关注药品库存水平和资源分配问题。

Little和Coughlan (2008)研究了库存需求问题，他们设计了一种约束规划模型以解决医院中与各产品和服务水平相关的库存需求问题。他们的模型可以决定在空间、运输和物品关键性限制下各物品的最优库存值，而这一模型在爱尔兰一家医院中针对贫乏和大体积物品的实验中得以验证。

Lapierre和Ruiz (2007)通过协调采购和分配业务，并平衡库存能力来处理医院物流问题。Jacobson等(2006)计算了为避免接种中断而需要的疫苗库存水平，而Swaminathan (2003)提出了一种多目标的启发式优化算法帮助将稀缺的药物分配给诊所，并考虑药物分配过程中的效率、有效性和公平性。

Rauner和Bajmoczy（2003）讨论了向奥地利不同地区分配医疗材料（半自动早期除颤器）的问题。这一问题考虑到除颤仪的购置和维修费用，紧急医疗技术人员的培训费用，心脏骤停患者的住院费用，出院患者的未来医疗费用，以及通过使用除颤器而提高的存活率和生活质量。他们为此开发了一个基于整数规划模型的决策支持系统。

Van de Klundert等（2008）发现，通过优化消毒部门和医院运营中心之间的无菌器械流动、简化流程、标准化材料，荷兰可以降低高达20%的成本。他们指出，这一问题的一般实例是NP-hard的，并提出了一个整数规划来刻画这一动态、非确定性模型。他们特别提到，通过开发一个涉及到运输和库存的成本极小化的方案来优化中央消毒部门和手术室之间的流动。对于这个问题的特定实例，他们使用动态规划来寻找多项式时间内的解决方案。

3.4 其他问题

一些研究者也关注了医疗领域的生产和管理问题。

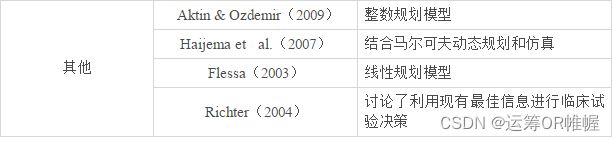
Aktin和Ozdemir（2009）从一维切割库存问题中开发了一种用于冠状动脉支架制造的两阶段方法。算法在第一阶段计算要切割的模式的数量，第二阶段寻找切割方案。这些问题受到需求、物资供应、正常工作时间以及加班时间和到期日的限制。他们用了两个整数规划模型，一个用于解决最小化修剪损失的问题，另一个用于最小化和材料投入、步骤数量、工时和逾期时间相关的总成本。

Haijema等人（2007）讨论了血库中血小板的生产和库存管理问题。他们将马尔可夫动态规划与仿真相结合，并将该方法应用到现实世界的荷兰血库这一案例中。

Flessa（2003）提出了一个线性规划模型，以分析在坦桑尼亚对一系列保健资源（预防、药品、保健中心、地区医院和区域医院）的最佳预算分配。他们讨论了五个不同的目标：最小化死亡案件数量、寿命损失、发病率、流行率和生活品质的下降。

Richter（2004）将重点放在临床试验上，并讨论了利用现有最佳信息进行决策，以弥补直到我们获得更好的信息这一时间段内的信息差距。他们表明将运筹学与健康经济学相结合，会对决策者的信息辅助起到巨大作用。

表2. 医疗管理和物流相关文献及其研究方法分类

 

 四 医疗实践

除了解决各种保健管理问题外，运筹学研究者还在药物治疗规划、传染病预防和控制、流行性疾病预防和控制、紧急反应和器官捐赠等方面作出了重大贡献。

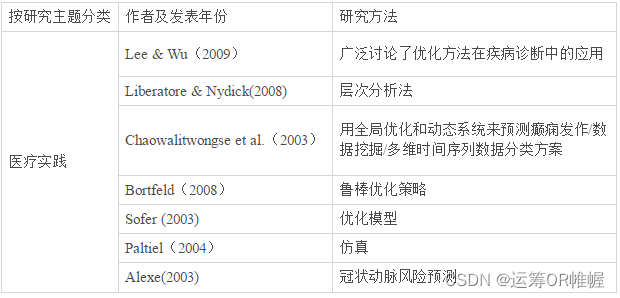
Lee和Wu（2009）广泛讨论了优化方法在疾病诊断中的应用。Liberatore和Nydick(2008)综述了层次分析法在医疗决策中的应用，他们总结了包括诊断、病人参与、治疗、器官移植 、项目和技术评估和选择、人力资源规划、医疗保健评估和政策在内的七个类别的50篇文献。

Chaowalitwongse等（2003）研究了脑异常活动，他们用全局优化和动态系统来预测癫痫发作，他们在2006年进一步研究，运用以优化为基础的数据挖掘技术，利用脑电图对大脑的正常活动和癫痫活动进行分类，研究结果表明我们有可能为诊断和治疗目的设计和开发有效的癫痫发作预警算法。在2008年，他们运用一种新的多维时间序列数据分类方案，用数学建模框架来尽量减少分类中的错误（或最大限度地提高准确性）。

癌症诊断是Bortfeld（2008）和Sofer (2003)等人工作的重点。前者研究了癌症患者放射治疗方面的不确定性，他们提出了一种鲁棒优化策略以推广此前的数学规划解法，同时讨论了从诊疗数据中得出的广泛的计算结果。后者提出了一种优化模型以确定最佳活检方案，即确定要进行活检的区域一最大限度的提高成功检测癌症的概率。

Paltiel（2004）引入了“哮喘策略模型”，作为一种马尔可夫状态转移模拟来预测哮喘的相关症状、急性恶化、预期寿命、医疗保健成本和成本效益。他们通过仿真模拟广泛探讨了10年期间内的结果。

最后，Alexe(2003)等研究了冠状动脉风险预测，他们介绍了数据的逻辑分析，并讨论了如何将其用于疾病预测。

 表3. 医疗实践相关文献及其研究方法分类

 五 结语

Papageorgiou (1978)是最早梳理运筹学在医疗问题中的应用的学者之一，他强调了医院的设计、运营和管理可以通过许多方式得到提高。从此，运筹学中的方法在一系列医疗优化问题中得到了成功的应用。通过解决潜在的优化问题，确定性模型和非确定性模型都被用来刻画现实世界的需求表现，并为分析和评估问题提供了系统性框架，这对规划、传输和管理问题起到了很大帮助。

总体而言，仿真和相关的非确定性方法在运筹学研究中占到15%。研究者主要关注医院准入机制、医院服务、患者康复、资源规划、设施利用率、物流、供应链协调、疫苗、紧急预防中涉及到的优化问题。另一方面，确定性方法主要涉及数学规划模型，并提供了列生成算法、影子价格、主问题/对偶问题、分支剪枝法、分支定界法、内点法等解决方案。动态规划模型在外科手术和急诊室排程、疫苗配方、容量规划有许多应用。

特别地，医疗中的许多问题由于其复杂性而无法用线性关系刻画，于是二次规划、梯度投影和凸规划等方法在放射治疗规划得到普遍应用，非线性的特征也被用于癫痫发作预警算法的设计。

当今研究中的一个有趣的方向是组合不同的运筹学方法来解决医疗中的复杂问题。神经网络已被用于优化放射治疗计划的线性规划模型(Wu et al., 2000)，模拟退火也被用作放射治疗规划的启发式优化方法(Webb, 1991; Shu et al., 1998)。

还一些具有前景却未受关注的研究领域包括情景规划、鲁棒优化和可靠性建模。特别地，适应性和可靠性方面对于医疗系统在容量限制和设施潜在关闭的情形下的表现十分关键。

参考文献

Blake, J. T., Dexter, F., & Donald, J. (2002). Operating room managers’ use of integer programming for assigning block time to surgical groups: a case study. Anesthesia & Analgesia, 94(1), 143-148.

Daskin, M. S., & Dean, L. K. (2005). Location of health care facilities. In Operations research and health care (pp. 43-76). Springer, Boston, MA.

De Grano, M. L., Medeiros, D. J., & Eitel, D. (2009). Accommodating individual preferences in nurse scheduling via auctions and optimization. Health Care Management Science, 12(3), 228.

Finarelli Jr, H. J., & Johnson, T. (2004). Effective demand forecasting in 9 steps: shifts in demand for a hospital's services can occur unexpectedly. Demand forecasting can help you prepare for these shifts and avoid strategic missteps. Healthcare Financial Management, 58(11), 52-58.

Henderson, S. G., & Mason, A. J. (2005). Ambulance service planning: simulation and data visualisation. In Operations research and health care (pp. 77-102). Springer, Boston, MA.

Rais, A., & Viana, A. (2011). Operations research in healthcare: a survey. International transactions in operational research, 18(1), 1-31.