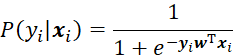数据分析-分类

目录

分类概念

评价指标

分类算法

逻辑回归

K近邻

决策树

朴素贝叶斯

高斯朴素贝叶斯GaussianNB()   

 伯努利朴素贝叶斯BernoulliNB()  

MultinomialNB

支持向量机

SVC

LinearSVC

---

分类概念

分类是对特征变量建模和预测的有监督学习方法。其中分类学习的目的是从给定的人工标注的分类训练样本数据集中学习出一个分类函数或者分类模型，也称作分类器（classifier）。当新的样本到来时，可以根据这个分类器进行预测，将新样本映射到特定的类别中。

对于分类，输入的训练数据包含信息有特征（Feature）和标签（label）。学习的本质就是找到特征与标签间的关系 。

分类预测模型是求取一个从输入变量 (特征)  到离散的输出变量（标签） 之间的映射函数。这样当有特征而无标签的未知样本输入时，可以通过映射函数预测未知数据的标签。

分类在消费者行为判断（根据以往用户的特征预测新用户是否会购买商品），信用风险评估（根据以往用户还款信息预测新用户是否会违约），医学诊断（根据CT的特征进行新冠肺炎的检测），电子邮件（根据邮件内容将邮件分为正常邮件/垃圾邮件）等领域得到广泛的应用。

评价指标

许多二分类问题中，正确率是常用的重要评价指标。但由于类别分布不平衡，仅正确率无法有效评价分类效果，需要借助召回率、精确率、F1等指标共同来评价模型效果。

混淆矩阵（设定1为正类、0为负类）

Confusion Matrix		预测标签
		1（正例）	0（负例）
真实标签	1（正例）	TP（真正样本数量）	FN（假负样本数量）
	0（负例）	FP（假正样本数量）	TN（真负样本数量）

正确率为分类正确的样本所占的比例=分类正确的样本数/中的样本数。
正确率(accuracy)=(TP+TN)/(TN+FN+FP+TP)

召回率为对应类别正确预测的样本数与该类总的样本数的比值，又称查全率。

1类召回率(recall)=TP/(TP+FN)

0类召回率(recall)=TN/(TN+FP)

精确率为对应类别正确预测的样本数与预测为该类的总的样本数的比值，又称查准率。

1类精确率(precision)=TP/(TP+FP)

0类精确率(precision)=TN/(TN+FN)

1=(2×精确率×召回率)/(精确率+召回率)

对应的有1类与0类的F1。

在分类问题中

由于不同的分类错误会导致不同的代价，如没有被新冠肺炎感染的人误诊为感染和新冠肺炎者误诊为没有感染所产生的代价完全不同；不同错误的代价不同导致对分类模型要求的指标不一样，有时为查准率、有时为查全率；可设置样本类别的权重与错误的代价成正比。

当类别不平衡，不同类别的样本数相差较大，可以对不同类别的样本设置不同的权重（代价），设置每个类别样本的权重与该分类在样本中出现的频率成反比。

分类算法

• 逻辑回归
• K近邻
• 决策树
• 朴素贝叶斯
• 支持向量机

逻辑回归

逻辑回归是采用回归分析的思想来解决分类问题的模型，通常解决的是二分类问题，通过引入一个Logistic函数，将连续型的输出映射到(0,1)之间。

逻辑回归模型的常用形式为：

 输出为样本属于某一类的概率。

from sklearn.linear_model import LogisticRegression
Lr = LogisticRegression()  # 模型构建（实例化对象）
Lr.fit(X_train,y_train)  # 模型训练
y_pred = clf.predict(test_x) # 模型预测
print("分类正确率（测试集）：",round(Lr.score(X_train,y_train),4))
print("分类正确率（训练集）：",round(Lr.score(X_train, y_train),4))
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))  # 输出主要分类指标的文本报告
'''
LogisticRegression使用说明：

LogisticRegression( penalty='l2', 
    *, 
    dual=False,
     tol=0.0001, 
    C=1.0,
    fit_intercept=True,
     intercept_scaling=1, 
    class_weight=None, 
    random_state=None, 
    solver='lbfgs', 
    max_iter=100, 
    multi_class='auto', 
    verbose=0, 
    warm_start=False, 
    n_jobs=None, 
    l1_ratio=None, 
)
''' 

K近邻

最近邻算法：

以全部训练样本作为代表点，计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的依据。

 

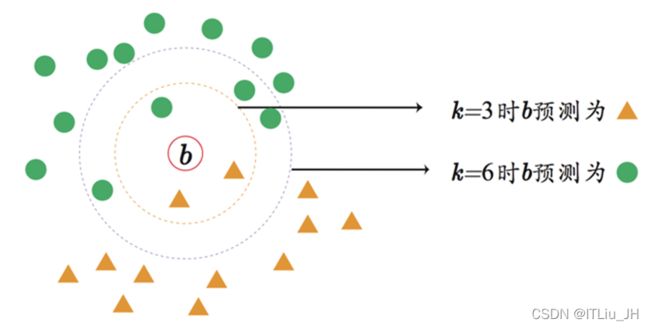
K-近邻（k nearest neighbor）算法：

最近邻算法对噪声数据过于敏感，为了解决这个问题，K-近邻（k nearest neighbor）算法把未知样本周边的K个最近样本计算在内，扩大参与决策的样本量，以避免个别数据直接决定决策结果。

算法流程：
1、确定K的大小和计算相似度（距离）的方法；#超参数确定
2、计算未知样本到所有训练样本的距离，找到与未知样本“最近” 的K个样本；
3、根据这K个训练样本的类别，采用多数投票的方式（或距离加权）来确定未知样本的类别。

加权K-近邻

对找出的K个“最近” 样本，每一个样本分配一个权重，使距离较近的样本的权重较大。

​​​​​​​K值的选择

当K值较大时，方差小；当K值较小时，方差大。

不同的K值可能导致不同的分类结果。

实现：

from sklearn.neighbors import KNeighborsClassifier
kn=KNeighborsClassifier()
kn.fit(train_x,train_y)
kn_pre=kn.predict(test_x)
kn.score(test_x,test_y)
print(classification_report(kn_pre,test_y))

'''
KNeighborsClassifier使用说明：

KNeighborsClassifier(
    n_neighbors=5,
    *,
    weights='uniform',
    algorithm='auto',
    leaf_size=30,
    p=2,
    metric='minkowski',
    metric_params=None,
    n_jobs=None,
    **kwargs,
)
'''

决策树

常用的决策树算法有三种：

CART（GINI index）

ID3 （信息增益）

C4.5 （信息增益率）

from sklearn.tree import DecisionTreeClassifier
dt=DecisionTreeClassifier(max_depth=5)
dt.fit(train_x,train_y)
dt_pre=dt.predict(test_x)
dt.score(test_x,test_y)
print(classification_report(dt_pre,test_y))

'''DecisionTreeClassifier使用说明：

DecisionTreeClassifier(
    *,
    criterion='gini',
    splitter='best',
    max_depth=None,
    min_samples_split=2,
    min_samples_leaf=1,
    min_weight_fraction_leaf=0.0,
    max_features=None,
    random_state=None,
    max_leaf_nodes=None,
    min_impurity_decrease=0.0,
    min_impurity_split=None,
    class_weight=None,
    ccp_alpha=0.0,
)
'''

朴素贝叶斯

算法过程：
1、计算每个类的先验概率；

P（Y1），P(Y2)
2、计算未知样本每个特征属性对于每个类别的条件概率

P(特征属性|Yi)

3、计算条件概率

P（X|Yi），X为未知样本，Yi未类别（i=1，2）（应用全概率公式，朴素贝叶斯的核心在于它假设特征的所有分量之间是独立的）。

4、计算P（X|Yi）*P（Yi）

5、判定X的类别

高斯朴素贝叶斯GaussianNB()   

主要面对输入为连续型的情况，通过假设高斯分布计算类条件概率。

伯努利朴素贝叶斯BernoulliNB()      

主要面对输入为离散型的情况，将特征二值化，例如一个词在文本中是否出现（1为是，0为否）。

多项式朴素贝叶斯MultinomialNB()        

主要面对输入为离散型的情况，例如一个词在不同文档中出现的次数。

高斯朴素贝叶斯GaussianNB()   

GNB=GaussianNB()
GNB.fit(train_x,train_y)
y_pred=GNB.predict(test_x)
GNB.score(test_x,test_y)
print(classification_report(test_y,y_pred))   
'''
GaussianNB(
*, 
priors=None, 
var_smoothing=1e-09
)

priors : array-like of shape (n_classes,)
    Prior probabilities of the classes. If specified the priors are not
    adjusted according to the data.

var_smoothing : float, default=1e-9
    Portion of the largest variance of all features that is added to
    variances for calculation stability.
'''

 伯努利朴素贝叶斯BernoulliNB()  

BNB=BernoulliNB()
BNB.fit(train_x,train_y)
y_pred=BNB.predict(test_x)
BNB.score(test_x,test_y)
print(classification_report(test_y,y_pred))
'''
BernoulliNB(*, alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)

alpha : float, default=1.0
    Additive (Laplace/Lidstone) smoothing parameter
    (0 for no smoothing).

binarize : float or None, default=0.0
    Threshold for binarizing (mapping to booleans) of sample features.
    If None, input is presumed to already consist of binary vectors.

fit_prior : bool, default=True
    Whether to learn class prior probabilities or not.
    If false, a uniform prior will be used.

class_prior : array-like of shape (n_classes,), default=None
    Prior probabilities of the classes. If specified the priors are not
    adjusted according to the data.

'''

MultinomialNB

MNB=MultinomialNB()
MNB.fit(train_x,train_y)
y_pred=MNB.predict(test_x)
MNB.score(test_x,test_y)
print(classification_report(test_y,y_pred))
'''
MultinomialNB(*, alpha=1.0, fit_prior=True, class_prior=None)
alpha : float, default=1.0
    Additive (Laplace/Lidstone) smoothing parameter
    (0 for no smoothing).

fit_prior : bool, default=True
    Whether to learn class prior probabilities or not.
    If false, a uniform prior will be used.

class_prior : array-like of shape (n_classes,), default=None
    Prior probabilities of the classes. If specified the priors are not
    adjusted according to the data.
'''

支持向量机

SVC

SVC_=SVC()
SVC_.fit(train_x,train_y)
y_pred=SVC_.predict(test_x)
SVC_.score(test_x,test_y)
print(classification_report(test_y,y_pred))

'''
SVC(
    *,
    C=1.0,
    kernel='rbf',
    degree=3,
    gamma='scale',
    coef0=0.0,
    shrinking=True,
    probability=False,
    tol=0.001,
    cache_size=200,
    class_weight=None,
    verbose=False,
    max_iter=-1,
    decision_function_shape='ovr',
    break_ties=False,
    random_state=None,
)
'''

LinearSVC

LSVC_=LinearSVC()
LSVC_.fit(train_x,train_y)
y_pred=LSVC_.predict(test_x)
LSVC_.score(test_x,test_y)
print(classification_report(test_y,y_pred))
'''
LinearSVC(
    penalty='l2',
    loss='squared_hinge',
    *,
    dual=True,
    tol=0.0001,
    C=1.0,
    multi_class='ovr',
    fit_intercept=True,
    intercept_scaling=1,
    class_weight=None,
    verbose=0,
    random_state=None,
    max_iter=1000,
)
'''