PyTorch的基本概念

什么是Pytorch，为什么选择Pytroch？

PyTorch是一个基于python的科学计算包，主要针对两类人群：

• 作为NumPy的替代品，可以利用GPU的性能进行计算
• 作为一个高灵活性、速度快的深度学习平台
• Pytorch相比Tensorflow而言，它的设计初衷是简单易用用，所以它是基于动态图进行实现的，从而方便调试。当然，Tensorflow在1.5版的时候就引入了Eager Execution机制实现了动态图，但它还是默认使用静态图。

配置Python环境

因为之前安装过了，所以没有细节的自己安装了，说一下大概流程。
首先是anaconda的安装，https://mirrors.tuna.tsinghua.edu.cn —> archive —> 根据自己的操作系统版本，如Windows 64位，可下载图中所示版本：Anaconda3-5.3.1-Windows-x86_64.exe.
然后就是配置你的显卡驱动，https://www.nvidia.com/Download/index.aspx?lang=en-us
然后安装CUDAhttps://developer.nvidia.com/cuda-downloads
然后安装CUDNNhttps://developer.nvidia.com/rdp/cudnn-download
具体可以参考这篇如何安装CUDA,CUDNN,TENSORFLOW（GPU）

Pytroch的安装

可以参考红色石头的这篇https://blog.csdn.net/red_stone1/article/details/86669362

PyTorch基础概念

• 张量

from __future__ import print_function
import torch

x=torch.rand(5,3)
#构造随机矩阵
print(x)
#构造0矩阵
x=torch.empty(5,3)
print(x)

x=torch.zeros(5,3,dtype=torch.long)
#构造一个填满0且数据类型为long的矩阵
print(x)

#直接从数据构造张量：
x=torch.tensor([5.5,3])
print(x)

x = x.new_ones(5, 3, dtype=torch.double)      # new_* methods take in sizes
print(x)
x = torch.randn_like(x, dtype=torch.float)    # 重载 dtype!
print(x)                                      # 结果有相同的size
print(x.size())

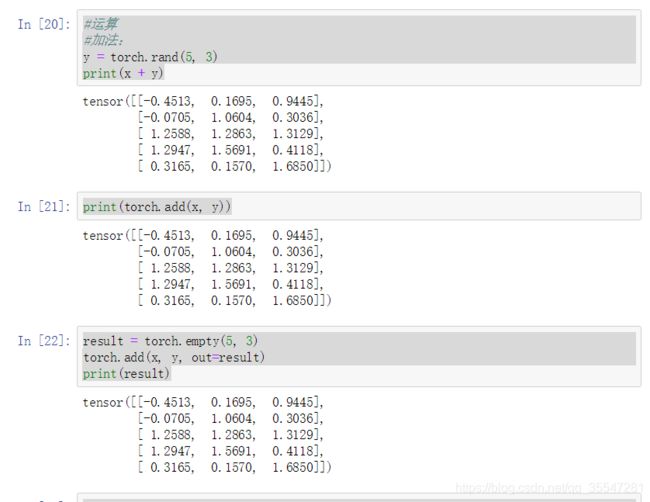
#运算
#加法：
y = torch.rand(5, 3)
print(x + y)
print(torch.add(x, y))
result = torch.empty(5, 3)
torch.add(x, y, out=result)
print(result)
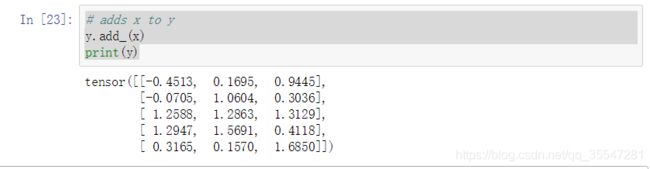
# adds x to y
y.add_(x)
print(y)

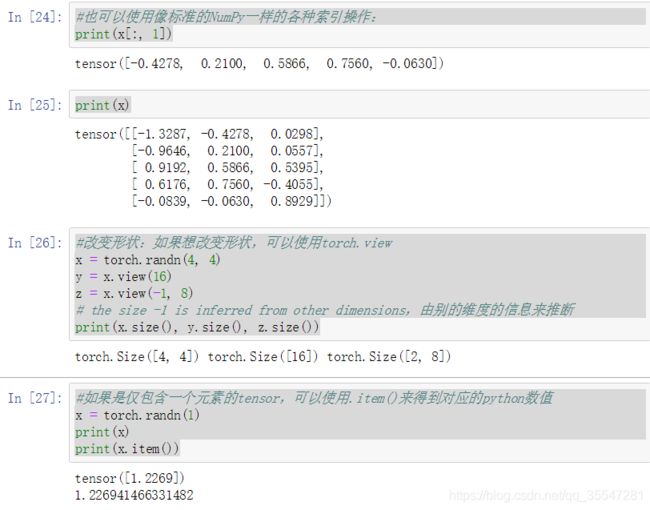
#也可以使用像标准的NumPy一样的各种索引操作：
print(x[:, 1])
print(x)
#改变形状：如果想改变形状，可以使用torch.view
x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8)  
# the size -1 is inferred from other dimensions，由别的维度的信息来推断
print(x.size(), y.size(), z.size())
#如果是仅包含一个元素的tensor，可以使用.item()来得到对应的python数值
x = torch.randn(1)
print(x)
print(x.item())

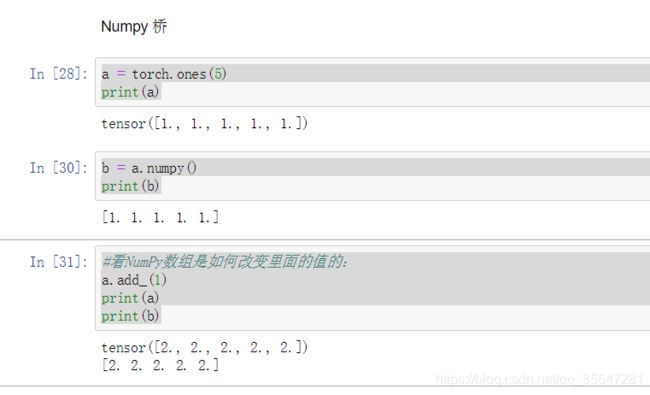
• numpy桥

a = torch.ones(5)
print(a)
b = a.numpy()
print(b)
#看NumPy数组是如何改变里面的值的：
a.add_(1)
print(a)
print(b)

• 将NumPy数组转化为Torch张量

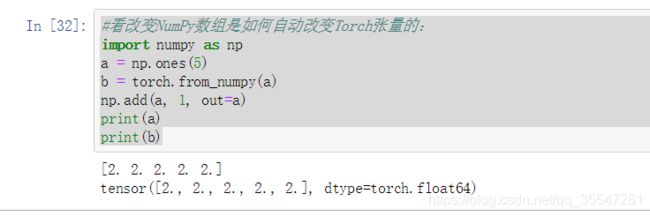
#看改变NumPy数组是如何自动改变Torch张量的：
import numpy as np
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)

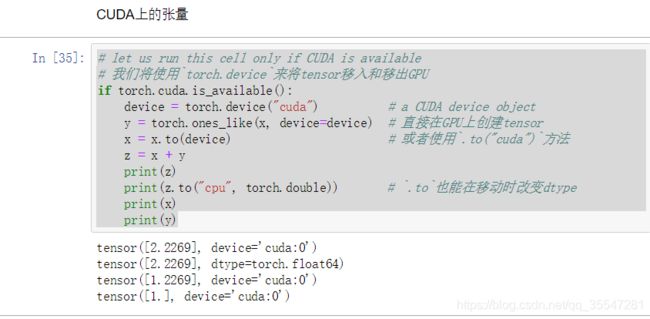
• CUDA上的张量

# let us run this cell only if CUDA is available
# 我们将使用`torch.device`来将tensor移入和移出GPU
if torch.cuda.is_available():
    device = torch.device("cuda")          # a CUDA device object
    y = torch.ones_like(x, device=device)  # 直接在GPU上创建tensor
    x = x.to(device)                       # 或者使用`.to("cuda")`方法
    z = x + y
    print(z)
    print(z.to("cpu", torch.double))       # `.to`也能在移动时改变dtype
    print(x)
    print(y)

先敷衍一波，怕来不及打卡
这是复制这位老哥的https://blog.csdn.net/herosunly/article/details/89036914
通过神经网络完成一个回归问题。其中样本数为64个，输入层为1000维，隐藏层为100，输出层为10维。

num_samples = 64 # N
dim_in, dim_hid, dim_out = 1000, 100, 10  # IN H OUT
x = torch.randn(num_samples, dim_in)  #  N * IN
y = torch.randn(num_samples, dim_out) #  N * OUT

# 提前定义模型
model = torch.nn.Sequential(
    torch.nn.Linear(dim_in, dim_hid, bias = False), #model[0]
    torch.nn.ReLU(),
    torch.nn.Linear(dim_hid, dim_out, bias = False),#model[2]
)

# torch.nn.init.normal_(model[0].weight) #修改一
# torch.nn.init.normal_(model[2].weight)

#提前定义loss函数和优化函数
loss_fun = torch.nn.MSELoss(reduction='sum')
eta = 1e-4 #修改二
optimizer = torch.optim.Adam(model.parameters(), lr=eta)


for i in range(1000):
  #Forward pass
  y_pred = model(x)
  
  #Loss
  loss = loss_fun(y_pred, y)
  print(it, loss.item())

  optimizer.zero_grad()
  # Backward pass
  loss.backward()

  # update model parameters
  optimizer.step()