论文笔记：WWW 2018 Variational Autoencoders for Collaborative Filtering

前言

论文链接：https://export.arxiv.org/pdf/1802.05814
github：https://github.com/dawenl/vae_cf

本文主要提出将变分自动编码器 variational autoencoders (vaes) 引入到协同过滤任务中，作者认为这种非线性概率模型可以超越线性因素模型有限的建模能力，同时线性因素模型在很大程度上主导着协同过滤。基于此，作者引入了一个多项式似然生成模型，并利用贝叶斯推理进行参数估计。尽管多项式似然在语言建模和经济学中得到了广泛的应用，但在推荐系统的研究中却很少受到关注。

1. Bag-of-words

Bag-of-words模型是信息检索领域常用的文档表示方法。

在信息检索中，BOW模型假定对于一个文档，忽略它的单词顺序和语法、句法等要素，将其仅仅看作是若干个词汇的集合，文档中每个单词的出现都是独立的，不依赖于其它单词是否出现。（是不关顺序的）

也就是说，文档中任意一个位置出现的任何单词，都不受该文档语意影响而独立选择的。那么到底是什么意思呢？那么给出具体的例子说明：

Wikipedia[1]上给出了如下例子:

John likes to watch movies. Mary likes too.

John also likes to watch football games.
根据上述两句话中出现的单词, 我们能构建出一个字典 (dictionary):

{“John”: 1, “likes”: 2, “to”: 3, “watch”: 4, “movies”: 5, “also”: 6, “football”: 7, “games”: 8, “Mary”: 9, “too”: 10}
该字典中包含10个单词, 每个单词有唯一索引, 注意它们的顺序和出现在句子中的顺序没有关联. 根据这个字典, 我们能将上述两句话重新表达为下述两个向量:

[1, 2, 1, 1, 1, 0, 0, 0, 1, 1]

[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]

这两个向量共包含10个元素, 其中第 $i$ 个元素表示字典中第 $i$ 个单词在句子中出现的次数. 因此BOW模型可认为是一种统计直方图 (histogram). 在文本检索和处理应用中, 可以通过该模型很方便的计算词频.

但是从上面我们也能够看出，在构造文档向量的过程中可以看到，我们并没有表达单词在原来句子中出现的次序（这也是bag of words的一个缺点，很多情况简单的用bow特征产生的结果就比较好了）

适用场景
现在想象在一个巨大的文档集合 $D$，里面一共有 $M$ 个文档，而文档里面的所有单词提取出来后，一起构成一个包含 $N$ 个单词的词典，利用Bag-of-words模型，每个文档都可以被表示成为一个N维向量。

变为 $N$ 维向量之后，很多问题就变得非常好解了，计算机非常擅长于处理数值向量，我们可以通过余弦来求两个文档之间的相似度，也可以将这个向量作为特征向量送入分类器进行主题分类等一系列功能中去。

总之通过有效的办法转换为向量之后，后面的一切都变得明朗起来了，因为至少得想办法让计算机理解。

2. Method

在本文中分别使用 $u\in \{1,\dots ,U\}$ 和 $i\in \{1,\dots ,I\}$ 代表用户集合和物品集合。其中用户恶化物品的交互矩阵为点击矩阵 $\mathbf{X}\in {\mathbb{N}}^{U\times I}$。值得注意的是 ${\mathbf{x}}_u=[x_{u1},\dots ,x_{uI}{]}^T\in {\mathbb{N}}^I$，其中内容为每一个物品对于用户点击的次数的BOW向量。

2.1 Model

对于每一个用户 $u$，模型首先通过标准的高斯分布采样一个 K 维的潜在表示 ${\mathbf{z}}_u$。之后这个潜在表示 ${\mathbf{z}}_u$ 通过一个非线性激活函数 $f_{\theta }(\cdot )$ 转换成 $\pi ({\mathbf{z}}_u)\in {\mathbb{R}}^I$ 来得到 $I$ 的概率分布。点击历史 ${\mathbf{x}}_u$ 的预测可以通过如下公式计算得到：
$$\begin{gathered} z_u\sim \mathcal{N}(0,{\mathbf{I}}_K), \\ \pi ({\mathbf{z}}_u)\propto exp\{f_{\theta }({\mathbf{z}}_u)\}, \\ {\mathbf{x}}_u\sim Mult(N_u,\pi ({\mathbf{z}}_u))\text{\hspace{1em}(1)} \end{gathered}$$
其中 非线性激活函数 $f_{\theta }(\cdot )$ 是以 $\theta$ 为参数的多层感知机。该多层感知机的输出经过一个 softmax 函数得到概率向量 $\pi ({\mathbf{z}}_u)\in {\mathbb{S}}^{I-1}$。其中 $N_u={\sum }_i{x}_{ui}$ 是用户 $u$ 所有点击次数的综合。基于 $N_u$ 和 $\pi ({\mathbf{z}}_u)$ ，可以通过从多项式 $\pi ({\mathbf{z}}_u)$ 中进行抽样得到 BOW 向量 ${\mathbf{x}}_u$。该生成模型对潜在因子模型进行了推广，通过将 $f_{\theta }(\cdot )$设为线性且使用高斯似然，就是经典的矩阵分解模型。

用户 $u$ 的对数似然(以潜在表示为条件)为:

$$log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)=\sum _i{x}_{ui}log{\pi }_i({\mathbf{z}}_u)\text{\hspace{1em}(2)}$$

该多项式似然常用于语言模型，如狄利克雷分布和经济学模型。它还被用于多类分类的交叉熵损失。例如，它已被用于基于会话的顺序推荐的递归神经网络。多项似然在诸如矩阵分解和自编码器等潜在因子模型的背景下研究得较少。本文的出发点是相信多项式分布很适合建模点击数据。点击矩阵(Eq. 2)的可能性奖励在 $x_u$ 的非零条目上，并且存在一定的局限性，因为 $\pi (z_u)$ 必须为1。因此，该模型应该为更有可能被点击的项目分配更多的概率质量。在一定程度上，它适用于 top-N 。通过比较，我们提出了两种常用的似然函数用于潜在因素协同过滤：高斯似然和逻辑似然。首先定义生成模型 $f_{\theta }(\cdot )$ 的输出 $f_{\theta }({\mathbf{z}}_u)=[f_{u1},\dots ,f_{uI}{]}^T$。对于用户 $u$ 的高斯对数似然为：
$$log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)=-\sum _i\frac{c_{ui}}{2}(x_{ui}-f_{ui}{)}^2\text{\hspace{1em}(3)}$$

本文引入一个“置信”权重 $c_{x_{ui}}=c_{ui}$，其中 $c_1>c_0$ 来平衡点击数据中未观察到的0。这也等价于用非加权高斯似然和负抽样训练模型。用户 $u$ 的逻辑对数似然为：
$$log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)=\sum _i{x}_{ui}log\sigma (f_{ui})+(1-x_{ui})log(1-\sigma (f_{ui}))\text{\hspace{1em}(4)}$$

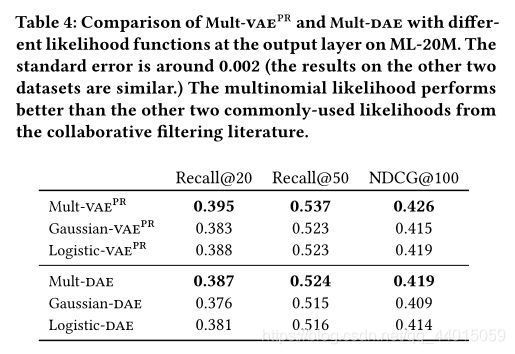
其中 $\sigma (x)=1/(1+exp(-x))$ 是logistic函数。在后文中将多项式似然与高斯似然以及逻辑似然进行了对比。

2.2 Variational inference ($Mult-VA{E}^{PR}$)

为了学习Eq. 1中的生成模型，来估计 $\theta$ ( $f_{\theta }(\cdot )$的参数)。为此需要近似每个数据点的后验分布 $p({\mathbf{z}}_u|{\mathbf{x}}_u)$。本文采用变分推理。变分推理用一种更简单的变分近似来估计真正的后验：
$$q({\mathbf{z}}_u)=\mathcal{N}({\mu }_u,diag\{{\sigma }_u^2\})$$

变分推理的目的是优化自由变分参数 $\{{\mu }_{\mu }，{\sigma }_u^2\}$，使KL散度 $KL(q({\mathbf{z}}_u)\Vert p({\mathbf{z}}_u|{\mathbf{x}}_u)$最小。

2.2.1 Amortized inference and the variational autoencoder

随着用户和物品的数量增多，用来优化 $\{{\mu }_u,{\sigma }_u^2\}$ 的参数量大大增加，这可能成为拥有数百万用户和项目的商业推荐系统的瓶颈。变分自编码器(vae)用一个依赖数据的函数(通常称为推理模型)替换单个变分参数:
$$g_{\varphi }({\mathbf{x}}_u)=[{\mu }_{\varphi }({\mathbf{x}}_u),{\sigma }_{\varphi }({\mathbf{x}}_u)]\in {\mathbb{R}}^{2K}$$
其中 ${\mu }_{\varphi }({\mathbf{x}}_u),{\sigma }_{\varphi }({\mathbf{x}}_u)$ 的维度均为 $K$。因此我们得到近似估计的表示形式为：
$$q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)=\mathcal{N}({\mu }_{\varphi }({\mathbf{x}}_u),diag\{{\sigma }_{\varphi }^2({\mathbf{x}}_u)\})$$
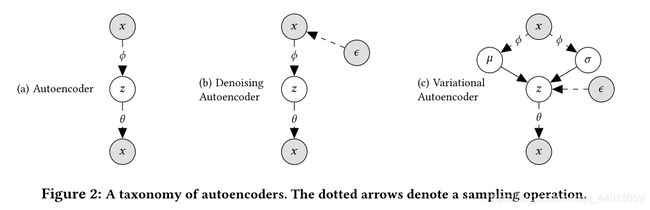
即推理模型以观测数据 ${\mathbf{x}}_u$ 作为输入，输出相应的变分分布 $q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)$ 的变分参数，优化后期望近似于 $p({\mathbf{z}}_u|{\mathbf{x}}_u)$。在图2c中将 $q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)$ 和生成模型 $p_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)$ 放在一起，最终得到了一个类似于自动编码器的体系结构——变分自动编码器。

损失函数：
$$\begin{gathered} logp({\mathbf{x}}_u;\theta )\ge {\mathbb{E}}_{q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)}[log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)]-KL(q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)||p({\mathbf{z}}_u)) \\ =\mathcal{L}({\mathbf{x}}_u;\theta ,\varphi )\text{\hspace{1em}(5)} \end{gathered}$$

$\mathcal{L}({\mathbf{x}}_u;\theta ,\varphi )$ 通常被称为 evidence lower bound （ELBO） 。ELBO 是 $\theta$ 和 $\varphi$ 的函数。可以通过采样 $z_u\sim q_{\varphi }$ 来获得 ELBO 的无偏估计，并执行随机梯度进行优化。然而不能简单地通过这个采样过程对 $\varphi$ 取梯度。解决方案是：对 $ϵ\sim \mathcal{N}(0.{\mathbf{I}}_K)$，并且 ${\mathbf{z}}_u={\mu }_{\varphi }({\mathbf{x}}_u)+ϵ\odot {\sigma }_{\varphi }({\mathbf{x}}_u)$。通过这样做，采样过程中的随机性被隔离，并且 $\varphi$ 的梯度可以通过采样的 $z_u$ 反向传播。
训练过程：

2.2.2 Alternative interpretation of ELBO

式（5）中的 ELBO 的第一项可以理解为(负)重构误差，第二项KL可以理解为正则化。进而引入权重参数 $\beta$ 调整正则化强度，进而可以表示为
$${\mathcal{L}}_{\beta }({\mathbf{x}}_u;\theta ,\mu )={\mathbb{E}}_{q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)}[log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)]-\beta \cdot KL(q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)||p({\mathbf{z}}_u))\text{\hspace{1em}(6)}$$

通过引入权重参数 $\beta$ 可以更好的拟合数据。如果 $\beta <1$，相当于削弱先验约束的影响，相当于 $\frac{1}{U}{\sum }_{u}q(\mathbf{z}|{\mathbf{x}}_u)\approx p(\mathbf{z})=\mathcal{N}(\mathbf{z};0;{\mathbf{I}}_k)$，这意味着该模型不太能够通过原始的抽样来生成新的用户历史记录。

但最终我们的目标是做出好的推荐，而不是最大化可能性或生成想象中的用户历史。因此，将 $\beta$ 作为自由正则化参数处理并产生显著的性能改进。对于超参 $\beta$ 的选择，作者提出了一个简单的启发式方法：开始训练时设置 $\beta =0$，并逐渐增加 $\beta$ 到1。线性退火 KL 项缓慢更新 $\theta$，$\varphi$ 和记录最佳 $\beta$ 时，其性能达到峰值。该方法不需要对不同 $\beta$ 值的多模型进行训练，这是一种训练 VAE 模型的启发式算法。

识别出基于峰值验证度量的最佳 $\beta$，我们可以用相同的退火方法重新训练模型，但在达到该值后停止增加 $\beta$(如图1中的红点虚线所示)。作者将这种部分正则化的 vae 用多项似然表示为 $Mult-VA{E}^{pr}$。

2.2.3 Computational Burden

之前的神经网络协同过滤模型采用随机梯度下降训练，在每一步中，从点击矩阵中随机抽取单个(用户、项目)条目来执行梯度更新。在算法1中，作者对用户进行子样本，并获取他们的整个点击历史(点击矩阵的完整行)来更新模型参数。这消除了通常用于(用户、项目)条目子抽样方案的负抽样(以及用于选择负示例数量的超参数调优)的必要性。

然而该方法带来的一个计算挑战是，当项目的数量很大时，计算 $\pi ({\mathbf{z}}_u)$ 的多项概率的计算成本较高，因为它需要为标准化计算所有项目的预测。这是语言建模中常见的挑战，因为词汇表的大小是几百万甚至更多。对于项目较大的数据集中，可以采用前人提出的归一化因子 $\pi ({\mathbf{z}}_u)$ 在一定程度上解决这个问题。

2.3 A taxonomy of autoencoders （$Mult-DAE$）

在第2.2节中介绍了在非线性生成模型下使用近似贝叶斯推理的最大似然边际估计(如式1)。从学习自动编码器的角度来理解此方法。最大似然估计在一个常规的自动编码器中采取以下形式
$$\begin{gathered} {\theta }^{AE},{\varphi }^{AE}=argma{x}_{\theta ,\varphi }\sum _u{\mathbb{E}}_{\delta ({\mathbf{z}}_u-g_{\varphi }({\mathbf{x}}_u))}[log{p}_{\theta }({\mathbf{x}}_u|{\mathbf{z}}_u)] \\ =argma{x}_{\theta ,\varphi }\sum _{u}log{p}_{\theta }({\mathbf{x}}_u|g_{\varphi }({\mathbf{x}}_u))\text{\hspace{1em}(7)} \end{gathered}$$:

有两个关键区别的注意:(1) auto-encoder (和去噪 auto-encoder )有效地优化 vae 的第一项(式（5）和式（6）)，具体来说使用一个 $\delta$ 变量分布 $q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)=\delta ({\mathbf{z}}_u-g_{\varphi }({\mathbf{x}}_u))$ —它不规范 $q_{\varphi }({\mathbf{z}}_u|{\mathbf{x}}_u)$ 对任何先验分布的影响。(2) $\delta ({\mathbf{z}}_u-g_{\varphi }({\mathbf{x}}_u))$ 是只有在$g_{\varphi }({\mathbf{x}}_u))$输出时的$\delta$分布。将此与vae相比较，后者的学习是使用一种变分分布，即 $g_{\varphi }({\mathbf{x}}_u))$ 输出高斯分布的参数(meanandvariance)。这意味着vae有能力捕获潜在状态 $z_u$ 中的每个数据点的差异。

在实践中，作者发现自编码器非常容易过拟合，因为网络学习把所有的概率权重放到 $x_u$ 中的非零项。通过在输入层引入dropout，去噪自编码器(DAE)不太容易过度拟合，同时模型性能良好。此外，作者还研究了一种具有多项似然的去噪自编码器。我们表示这个模型为 $Multi-VA{E}^{PR}$。

2.4 Prediction

以 $Mult-VA{E}^{PR}$ 为例说明在基于此生成模型得到最终的预测结果。给定用户的点击历史记录 $\mathbf{x}$，根据未标准化的预测多项式概率 $f_{\theta }(\mathbf{z})$ 对所有物品进行排序。对 $\mathbf{x}$ 的潜表示 $\mathbf{z}$ 构造如下：对于$Mult-VA{E}^{PR}$，只需取变分分布 $\mathbf{z}={\mu }_{\varphi }(\mathbf{x})$ 的均值;对于 $Mult-DAE$，取输出 $\mathbf{z}=g_{\varphi }(\mathbf{x})$。

使用自动编码器的优点很容易看出。通过对推理模型(编码器) $g_{\varphi }(\cdot )$ 和生成模型(解码器) $f_{\theta }(\cdot )$ 两个函数进行评估，可以有效地对用户进行预测。对于大多数协同过滤模型，如矩阵分解，当给定训练数据中不存在的用户点击历史时，通常需要进行某种形式的优化，以获得该用户的潜在因子。这使得自动编码器的使用在工业应用中特别有吸引力，在工业应用中，高效地进行预测和低延迟是很重要的。

3. Experiment