PyTorch项目笔记（一）MNIST数字识别

MNIST数字识别是学习神经网络非常好的入门知识。MNIST是由YannLeCun等创建的手写数字识别数据集，简单易用，通过对该数据集的认识可以很好地对数据进行神经网络建模。

1 MNIST数据集

MNIST数据集主要是一些手写的数字图片及对应标签，该数据集的图片共有10类，分别对应阿拉伯数字0~9。数据集示例如下图所示。

2 导入数据集

1. 使用DataLoader对数据进行封装，PyTorch会在root目录下检测数据是否存在，当数据不存在时，则自动将数据下载到data目录中。
2. 使用ToTensor()将0 ~ 255的像素值映射到0 ~ 1的范围内，并转化为Tensor格式。
3. 使用Normalize(mean, std)方法实现归一化。不同数据集中的图像通道对应的均值（mean）和标准差（std）是不同的。MNIST数据集的均值是0.1307，标准差是0.3081，这些系数是数据集提供方提供的，有利于加速神经网络的训练。
4. 随机取出一个batch下的数据进行观察。

import numpy as np
import torch
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import torchvision

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST(root='./data', #root表示数据加载的相对目录
                   train=True, #train表示是否加载数据库的训练集，False时加载测试集
                   download=True,#download表示是否自动下载
                   transform=transforms.Compose([#transform表示对数据进行预处理的操作
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),batch_size=64, shuffle=True)#batch_size表示该批次的数据量  shuffle表示是否洗牌
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./data', train=False, transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),batch_size=64, shuffle=True)

def imshow(img):
    img = img / 2 + 0.5     # 逆归一化
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    plt.show()

# 得到batch中的数据
dataiter = iter(train_loader)
images, labels = dataiter.next()

# 展示图片
imshow(torchvision.utils.make_grid(images))

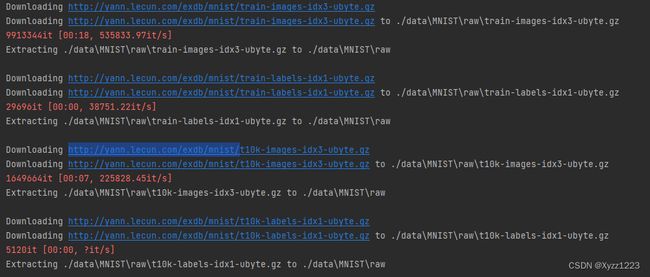
数据集的下载过程如下图所示。

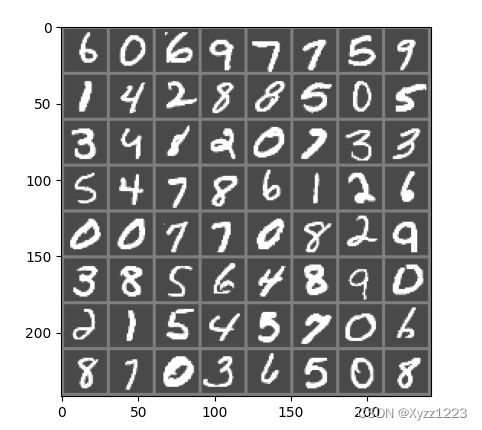
一个batch下的数据如下图所示。

3 构建模型

一个典型的神经网络训练过程包括以下步骤：

• 定义神经网络
• 前向传播
• 计算损失
• 反向传播
• 更新参数

3.1 定义神经网络

针对MNIST数据集，本文构建了一个简单的图像识别网络，网络结构图如下所示。

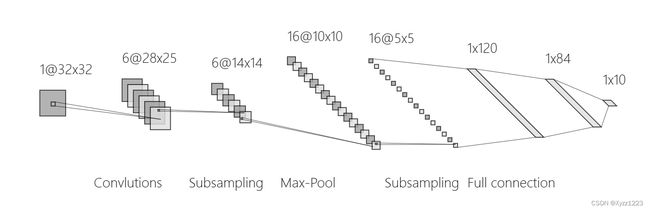
这是一个简单的前馈神经网络，其中Convolutions是卷积操作；Subsampling是下采样操作，也就是池化；Full connection 表示全连接层。该网络将输入的图片，经过两层卷积和池化，再经过三层全连接层，最后输出图片对应每个阿拉伯数字的概率。代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F#可以调用一些常见的函数，例如非线性以及池化等

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # 输入图片是1 channel输出是6 channel 利用5x5的核大小
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 全连接 从16 * 4 * 4的维度转成120
        self.fc1 = nn.Linear(16 * 4 * 4, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
    def forward(self, x):
        # 在(2, 2)的窗口上进行池化
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)#(2,2)也可以直接写成数字2
        x = x.view(-1, self.num_flat_features(x))#将维度转成以batch为第一维 剩余维数相乘为第二维
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x
    def num_flat_features(self, x):
        size = x.size()[1:]  # 第一个维度batch不考虑
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

输出结果如下：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=256, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

3.2 前向传播

定义完一个网络结构之后，我们将所有数据按照batch的方式进行输入，得到对应的网络输出，这就是所谓的前向传播。此处随机取出2张图片进行观察，代码如下：

image = images[:2]
label = labels[:2]
print(image.size())
print(label)
out = net(image)
print(out)

运行结果如下：

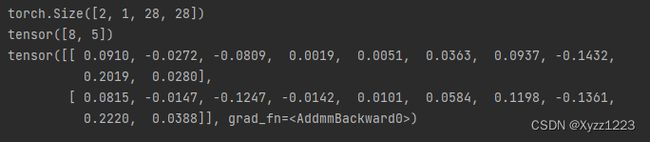
观察运行结果可知，随机取出的图片是数字8和5。最后输出的维度为10的tensor，每个位置上的数值代表成为该类别的概率值。以第二张图片为例，第二张图片为数字8的概率最大，与实际数字5不一致。输出结果与实际情况不符的原因是目前网络没有进行训练，只是随机初始化了结构中的权重，所以输出暂时没有参考价值。

3.3 计算损失

损失函数需要一对输入：模型输出与目标，用于评估输出距离目标有多远。损失用loss来表示，损失函数的作用就是计算神经网络每次迭代的前向计算结果与真实值之间的超级，从而指导模型下一步训练网正确的方向进行。常见的损失函数有交叉熵损失函数和均方误差损失函数。
在PyTorch中，nn库模块提供了多种损失函数，常见的有以下几种：

• 回归问题：nn.MSELoss()
• 二分类问题：nn.BCELoss()
• 多分类问题：nn.CrossEntropyLoss()
  由于MNIST数据集是十个分类，因此选择nn.CrossEntropyLoss()，代码如下：

image = images[:2]
label = labels[:2]
out = net(image)
criterion = nn.CrossEntropyLoss()
loss = criterion(out, label)
print(loss)

运行结果如下图所示：

结果表明当前两个样本通过网络输出后与实际差距仍有2.3134，我们的训练目标是最小化loss值。

3.4 反向传播与参数更新

当计算出一次前向传播loss值之后，可进行反向传播计算梯度，以此来更新参数。在Pytorch中，对loss调用backward()即可。backward(0函数束语torch.autograd函数库，在深度学习过程中进行反向传播，计算输出变量关于输入变量的梯度。最后要做的就是更新神经网络的参数，最简单的规则就是随机梯度下降，公式如下：
$$weight=weight-learningRate\times gradient$$
示例代码如下：

#创建优化器
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.01)#lr代表学习率
criterion = nn.CrossEntropyLoss()
# 在训练过程中
image = images[:2]
label = labels[:2]
optimizer.zero_grad()   # 消除累积梯度
out = net(image)
loss = criterion(out, label)
loss.backward()
optimizer.step()    # 更新参数

4 模型训练

未来方便后续继续使用模型，可将训练过程封装成一个函数，像该函数传入网络模型、损失函数、优化器等必要对象后，在MNIST数据集上进行训练并打印日志观察过程，代码如下：

def train(n):
    net.train()  # 设置为training模式
    for epoch in range(n):
        running_loss = 0.0
        for i, data in enumerate(train_loader):
            # 得到输入 和 标签
            inputs, labels = data
            # 消除梯度
            optimizer.zero_grad()
            # 前向传播 计算损失 后向传播 更新参数
            outputs = net(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()
            # 打印日志
            running_loss += loss.item()
            if i % 100 == 0:    # 每100个batch打印一次
                print('[%d, %5d] loss: %.3f' %
                      (epoch + 1, i + 1, running_loss / 100))
                running_loss = 0.0

train(2)#此处表示训练两轮

运行结果如下图所示，从结果中可以看出训练过程中loss值不断下降：

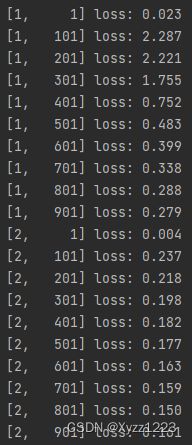
5 模型评估

在训练完成之后为了检验模型的训练结果，可以在测试集上进行验证，通过不同的评估方法进行评估。分类模型的常见评估方法是进求分类准确率，它能衡量所有类别中预测正确的个数占所有样本的比值，代码如下：

correct = 0
total = 0
with torch.no_grad():#或者model.eval()
    for data in test_loader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (100 * correct / total))

训练时用的是train loader数据集,测试时就得用另一部分的数据集 test_loader。代码中用到 with torch.no gradO、是为了让植刑不进行梯度求导,和modeLeval()具有相同的作用。eval即evaluation模式，train即训练模式，这两种模式仅仅当模型中有 Dropout和 BatchNorm时才会有影响。因为训练时 Dropout和 BatchNorm都会开启，而一般而言，测试时 Dropout会被关闭,BatchNorm中的参数也是利用训练时保留的参数，所以测试时应进入评估模式。通过数据输入神经网络，得到神经网络的概率输出后，我们需要取最大值对应的索引作为预测，这里用到了torch.max函数。该函数接收两个输入，一个是数据，另一个是表示要在哪一维度操作，很明显这里输入的是概率值及第二维的1。返回两个输出，即最大的数值及最大值对应的索引。

6 结果测试

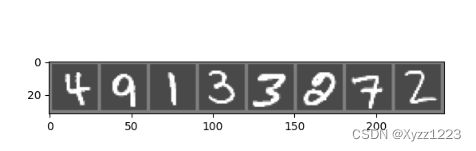
我们随机取出8张数字图片进行测试，代码如下：

image = images[:8]
label = labels[:8]
imshow(torchvision.utils.make_grid(image))
print("数字图片标签值：", end="")
print(label)
out = net(image)
out_label = []
for m in out:
    t = torch.argmax(m).item()
    out_label.append(t)
print("神经网络预测值：", end="")
print(out_label)

运行结果如下图所示：