数字图像处理——频域滤波基础
频域滤波基础
1、频域滤波与空域滤波的关系
傅立叶变换可以将图像从空域变换到频域,而傅立叶反变换则可以将图像的频谱逆变换为空域图像。这样一来,我们可以利用空域图像与频域之间的对应关系,尝试将空域卷积滤波变换为频域滤波,而后再将频域滤波处理后的图像再反变换回空间域,从而达到图像增强的目的。这样做的一个最主要的吸引力在于频域滤波的直观性特点。
根据著名的卷积定理,两个二维连续函数在空间域中的卷积可由其相应的两个傅立叶变换乘积的反变换而得到;反之,在频域中的卷积可由在空间域中乘积的傅立叶变换而得到,即:
f ( x , y ) ∗ h ( x , y ) ⟺ F ( u , v ) H ( u , v ) f(x,y)*h(x,y) \iff F(u,v)H(u,v) f(x,y)∗h(x,y)⟺F(u,v)H(u,v)
f ( x , y ) h ( x , y ) ⟺ F ( u , v ) ∗ H ( u , v ) f(x,y)h(x,y) \iff F(u,v)*H(u,v) f(x,y)h(x,y)⟺F(u,v)∗H(u,v)
其中,F(u,v) 和 H(u,v) 分别表示 f(x,y) 和 h(x,y) 的傅立叶变换,而符号表示傅立叶变换对。
式(1) 构成了整个频域滤波的基础。
2、频域滤波的基本步骤
根据式(1) 进行频域滤波通常应遵循以下步骤:
- 计算原始图像 f(x,y) 的 DFT,得到频谱 F(u,v);
- 将频谱 F(u,v) 的零频点移动到频谱图的中心位置;
- 计算滤波器函数 H(u,v) 与 F(u,v) 的乘积 G(u,v);
- 将频谱 G(u,v) 的零频点移回到频谱图的左上角位置;
- 计算第 (4) 步计算结果的傅立叶反变换 g(x,y);
- 取 g(x,y) 的实部作为最终滤波后的结果图像。
由上面叙述可知,滤波能否取得理想的关键取决于频域滤波函数 H(u,v)。常常称之为滤波器,或滤波器传递函数,因为它在滤波中抑制或滤除了频谱中某些频率的分量,而保留其他的一些频率不受影响。在这里只关心其值为实数的滤波器,这样滤波过程中 H 的每一个实数元素分别乘以 F 中对于位置的复数元素,从而使 F 中元素的实部和虚部等比例的变化,不会改变 F 的相位谱,这种滤波器也因此称为 “零相位” 滤波器。这样,最终反变换回空间域得到的滤波结果图像 g(x,y) 理论上也应当为实函数。然而由于计算舍入误差等原因,可额能会有非常小的虚部,通常将虚部直接忽略。
3、频域滤波的 Matlab 实现
编写了一个 imfreqfilt 函数:
function out = imfreqfilt(I,ff)
%imfreqfilt函数 对灰度图像进行频域滤波
%参数I 输入的空域图像
%参数ff 应用的与原图像等大的频域滤镜
if (ndims(I)==3) && (size(I,3)==3) % RGB图像
I = rgb2gray(I);
end
if (size(I) ~= size(ff))
msg1 = sprintf('%s: 滤镜与原图像不等大,检查输入', mfilename);
msg2 = sprintf('%s: 滤波操作已经取消', mfilename);
eid = sprintf('Images:%s:ImageSizeNotEqual',mfilename);
error(eid,'%s %s',msg1,msg2);
end
% 快速傅立叶变换
f = fft2(double(I));
% 移动原点
s = fftshift(f);
% 应用滤镜及反变换
out = s .* ff; %对应元素相乘实现频域滤波
out = ifftshift(out);
out = ifft2(out);
% 求模值
out = abs(out);
% 归一化以便显示
out = out/max(out(:));
end
4、频率低通滤波器
在频谱中,低频主要对应图像在平滑区域的总体灰度级分布,而高频对应图像的细节部分,如边缘和噪声。因此,图像平滑可以通过衰减图像频谱中的高频部分来实现,这就建立了空间域图像平滑和频域低通滤波之间对应关系。
4.1、理想低通滤波器及其实现
4.4.1、理论基础
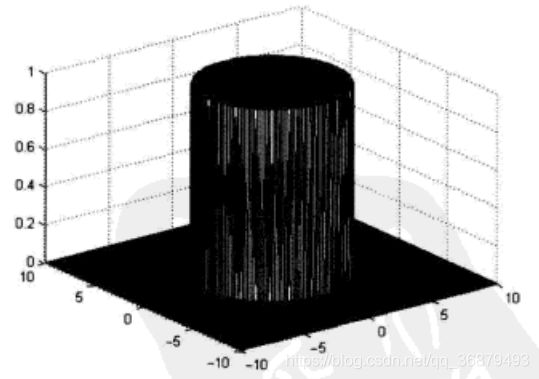
最容易想到的衰减高频成份的方法就是咋一个称为 “截止频率” 的位置 “截断” 所有的高频成份,将图像频谱中所有高于这一截断频率的频谱成份设为 0,低于截止频率的成份设为保持不变。能够达到这种效果的滤波器如图:
如果图像的宽度为 M,高度为 N,那么理想低通滤波器可形式化地描述为:
H ( u , v ) = { 1 , [ ( u − M 2 ) 2 + ( v − N 2 ) 2 ] ≤ D 0 0 , [ ( u − M 2 ) 2 + ( v − N 2 ) 2 ] ≥ D 0 H(u,v)=\begin{cases}1,[(u-\frac{M}{2})^2+(v-\frac{N}{2})^2]\leq D_0 \\ 0,[(u-\frac{M}{2})^2+(v-\frac{N}{2})^2]\ge D_0 \end{cases} H(u,v)={1,[(u−2M)2+(v−2N)2]≤D00,[(u−2M)2+(v−2N)2]≥D0
其中,D0 表示理想低通滤波器的截止频率,滤波器的频率域原点在频谱图像的中心处,在以截止频率为半径的圆形区域之内的滤镜元素值全部为 1,而该圆之外的滤镜元素值全部为 0。理想低通滤波器的频率特性在截止频率处十分陡峭,无法用硬件实现,这也是我们称之为理想的原因。
理想低通滤波器可在一定程度上去除图像噪声,但由此带来的图像边缘和细节的模糊效应也是较为明显,其效果类似于均值滤波。
4.4.2、Matlab 实现
编写了一个 imidealflpf 函数可以得到截止频率为 freq 的理想低通滤波器:
function ff = imidealflpf(I, freq)
% imidealflpf函数 构造理想的频域低通滤波器
% I参数 输入的灰度图像
% freq参数 低通滤波器的截止频率
% 返回值 ff 与I等大的频域滤镜
[M,N] = size(I);
ff = ones(M, N);
for i = 1:M
for j = 1:N
if (sqrt (((i-M/2)^2 + (j-N/2)^2 ))>freq)
ff(i,j)=0; %高于截止频率 设为0
end
end
end
【例】理想低通滤波器的实现
img = imread('lena_Rician10.bmp');
%生成滤镜 截止频率为20
ff = imidealflpf(img,20);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为40
ff = imidealflpf(img,40);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80
ff = imidealflpf(img,80);
out2 = imfreqfilt(img,ff);
figure;
subplot(2,4,1);
imshow(img);
title('原图');
subplot(2,4,2);
imshow(out);
title('截止频域为20');
subplot(2,4,3);
imshow(out1);
title('截止频率为40');
subplot(2,4,4);
imshow(out2);
title('截止频率为80');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
subplot(2,4,5);
imshow(f,[]);
title('原图对应的频谱');
subplot(2,4,6);
imshow(f1,[]);
title('freq = 20 的图像对应的频谱');
subplot(2,4,7);
imshow(f2,[]);
title('freq = 40 的图像对应的频谱');
subplot(2,4,8);
imshow(f3,[]);
title('freq = 80 的图像对应的频谱');
当截止频率非常低时,只有非常靠近原点的低频成份能够通过,图像模糊严重;截止频率非常高,通过的频率成份就越多,图像模糊的程度就越小,所获得的图像也就越接近原图像。但可以看出,理想低通滤波器不能很好地兼顾噪声滤除与细节保留这两方面。
4.2、高斯低通滤波器及其实现
4.2.1、理论基础
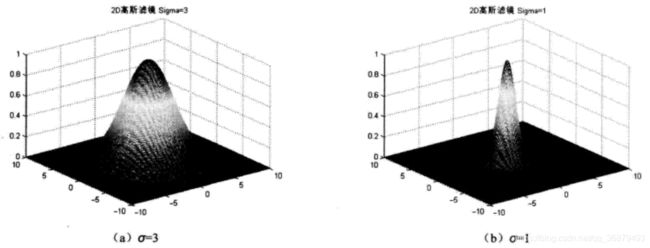
高斯低通滤波器的频域二维形式由下式给出:
H ( u , v ) = e − [ ( u − M 2 ) 2 + ( v − N 2 ) 2 ] / 2 σ 2 H(u,v)=e^{-[(u-\frac{M}{2})^2+(v-\frac{N}{2})^2]/2\sigma^2} H(u,v)=e−[(u−2M)2+(v−2N)2]/2σ2
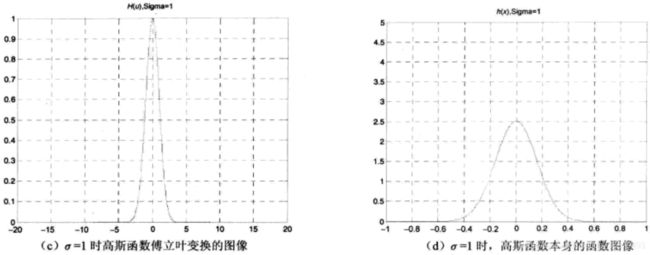
高斯函数具有相对简单的形式,而且它的傅立叶变换和傅立叶反变换都是实高斯函数。为了简单起见,下面给出一个一维高斯函数的傅立叶变换和傅立叶反变换作为例子。式(5) 告诉我们一维高斯函数的傅立叶正变换和反变换仍为高斯函数。
H ( u ) = A e − u 2 2 σ 2 ⟺ h ( x ) = 2 π σ A − 2 π 2 σ 2 x 2 H(u)=Ae^{-\frac{u^2}{2\sigma^2}} \iff h(x)=\sqrt{2\pi\sigma}A^{-2\pi^2\sigma^2x^2} H(u)=Ae−2σ2u2⟺h(x)=2πσA−2π2σ2x2
式中:σ 是高斯曲线的标准差。
频域和与之对应的空间域一维高斯函数的图形如下:
当 σ 增大时,H(u) 的图像倾向于变窄,而 h(x) 的图像倾向于变窄和变高。这也体现了频率域和空间域的对应关系。频率域滤波器越窄,滤波的高频成份越多,图像就越平滑(模糊);而在空间域,对应的滤波器就越窄,相应的卷积模板越平坦,平滑(模糊)效果就越明显。
下图给出了 σ 取值为 3 和 1 时的频域二维高斯滤波器的三维曲面表示,可以看出和二维高斯滤波器拥有同样的特点。
4.2.2、Matlab 实现
编写 imgaussflpf 函数:
function ff = imgaussflpf(I,freq,n)
% imbutterworthflpf函数 构造布特沃斯的频域低通滤波器
% I参数 输入的灰度图像
% freq参数 低通滤波器的截止频率
% n参数 阶数
% 返回值 ff 与I等大的频域滤镜
[M,N] = size(I);
ff = ones(M,N);
for i = 1:M
for j = 1:N
ff(i,j) = 1/(1 + (sqrt((i - M/2)^2 + (j - N/2)^2)/freq)^(2*n));
end
end
【例】实现高斯低通滤波
img = imread('lena_Rician10.bmp');
%生成滤镜 截止频率为20,阶数为2
ff = imgaussflpf(img,20,2);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为20,阶数为5
ff = imgaussflpf(img,20,5);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80,阶数为2
ff = imgaussflpf(img,80,2);
out2 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80,阶数为5
ff = imgaussflpf(img,80,5);
out3 = imfreqfilt(img,ff);
figure;
subplot(2,5,1);
imshow(img);
title('原图');
subplot(2,5,2);
imshow(out);
title('freq = 20,n = 2');
subplot(2,5,3);
imshow(out1);
title('freq = 20,n = 5');
subplot(2,5,4);
imshow(out2);
title('freq = 80,n = 2');
subplot(2,5,5);
imshow(out3);
title('freq = 80,n = 5');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
f4 = fft2(out3);
f4 = abs(fftshift(f4)); % 频谱
f4 = log(1 + f4); %压缩频率的范围
subplot(2,5,6);
imshow(f,[]);
title('原图对应的频谱');
subplot(2,5,7);
imshow(f1,[]);
title('freq = 20,n = 2的频谱');
subplot(2,5,8);
imshow(f2,[]);
title('freq = 20,n = 5的频谱');
subplot(2,5,9);
imshow(f3,[]);
title('freq = 80,n = 2的频谱');
subplot(2,5,10);
imshow(f4,[]);
title('freq = 80,n = 5的频谱');
5、频率域高通滤波器
图像锐化可以通过衰减图像频谱中的低频成份来实现,这就建立了空间域图像锐化与频域高通滤波之间对应关系。
5.1、高斯高通滤波器及其实现
对应于高斯低通滤波器:
H ( u , v ) = 1 − e − [ ( u − M 2 ) 2 + ( v − N 2 ) 2 ] / 2 σ 2 H(u,v)=1-e^{-[(u-\frac{M}{2})^2+(v-\frac{N}{2})^2]/2\sigma^2} H(u,v)=1−e−[(u−2M)2+(v−2N)2]/2σ2

5.1.1、Matlab 实现
编写 imgaussfhpf 函数:
function ff = imgaussfhpf(I,sigma)
% imgaussfhpf函数 构造高斯的频域低通滤波器
% I参数 输入的灰度图像
% sigma参数 高斯函数的sigma
% 返回值 ff 与I等大的频域滤镜
[M,N] = size(I);
ff = ones(M,N);
for i = 1:M
for j = 1:N
ff(i,j) = 1 - exp(-((i - M/2).^2 + (j - N/2).^2) / 2 /(sigma.^2));
end
end
【例】实现高斯高通滤波器
img = imread('lena_Rician10.bmp');
%生成滤镜 截止频率为20
ff = imgaussfhpf(img,20);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为40
ff = imgaussfhpf(img,40);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80
ff = imgaussfhpf(img,80);
out2 = imfreqfilt(img,ff);
subplot(2,4,1);
imshow(img);
title('原图');
subplot(2,4,2);
imshow(out);
title('sigma = 20');
subplot(2,4,3);
imshow(out1);
title('sigma = 40');
subplot(2,4,4);
imshow(out2);
title('sigma = 80');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
subplot(2,4,5);
imshow(f,[]);
title('原图对应的频谱');
subplot(2,4,6);
imshow(f1,[]);
title('sigma = 20的频谱');
subplot(2,4,7);
imshow(f2,[]);
title('sigma = 40的频谱');
subplot(2,4,8);
imshow(f3,[]);
title('sigma = 80的频谱');
高斯高通滤波器可以较好地提取图像中的边缘信息,σ 参数取值越小,边缘信息提取越不精确,会包含越多的非边缘信息;σ 参数取值越大,边缘提取越精确,但可能包含不完整的边缘信息。
5.2、频域拉普拉斯滤波器及其实现
5.2.1、理论基础
频域拉普拉斯算子的推导可以从一维开始,由傅立叶变换的性质可知:
F F T [ d n f ( x ) d x n ] = ( j u ) n F ( u ) FFT[\frac{d^nf(x)}{dx^n}]=(ju)^nF(u) FFT[dxndnf(x)]=(ju)nF(u)
因此拉普拉斯算子的傅立叶变换计算如下:
F F T [ ∂ 2 f ( x , y ) ∂ x 2 + ∂ 2 f ( x , y ) ∂ y 2 ] = ( j u ) 2 F ( u , v ) + ( j v ) 2 F ( u , v ) = − ( u 2 + v 2 ) F ( u , v ) FFT[\frac{\partial^2f(x,y)}{\partial x^2}+\frac{\partial^2f(x,y)}{\partial y^2}]=(ju)^2F(u,v)+(jv)^2F(u,v)=-(u^2+v^2)F(u,v) FFT[∂x2∂2f(x,y)+∂y2∂2f(x,y)]=(ju)2F(u,v)+(jv)2F(u,v)=−(u2+v2)F(u,v)
因此有下式成立:
F F T [ ∇ 2 f ( x , y ) ] = − ( u 2 + v 2 ) F ( u , v ) FFT[\nabla^2f(x,y)]=-(u^2+v^2)F(u,v) FFT[∇2f(x,y)]=−(u2+v2)F(u,v)
也即频域的拉普拉斯滤波器为:
H ( u , v ) = − ( u 2 + v 2 ) H(u,v)=-(u^2+v^2) H(u,v)=−(u2+v2)
根据频域图像频率原点的平移规律,将上式改写为:
H ( u , v ) = − [ ( u − M 2 ) 2 + ( v − N 2 ) 2 ] H(u,v)=-[(u-\frac{M}{2})^2+(v-\frac{N}{2})^2] H(u,v)=−[(u−2M)2+(v−2N)2]
5.2.2、Matlab 实现
编写 imlapf 函数:
function out = imlapf(I)
%imlapf 函数 构造频域拉普拉斯滤波器
%I 参数 输入的灰度图像
[M, N] = size(I);
out = ones(M, N);
for i = 1:M
for j = 1:N
out(i, j) = -((i-M/2)^2+(j-N/2)^2);
end
end
end
【例】拉普拉斯滤波实现
img = imread('lena.BMP');
%生成滤镜
ff = imlapf(img);
out = imfreqfilt(img,ff);
figure;
subplot(2,2,1);
imshow(img);
title('原图');
subplot(2,2,2);
imshow(out);
title('laplace滤波图像');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
subplot(2,2,3);
imshow(f,[]);
title('原图对应的频谱');
subplot(2,2,4);
imshow(f1,[]);
title('laplace滤波图像对应的频谱');
6、Matlab 综合案例——利用频域滤波消除周期噪声
6.1、频域带阻滤波器
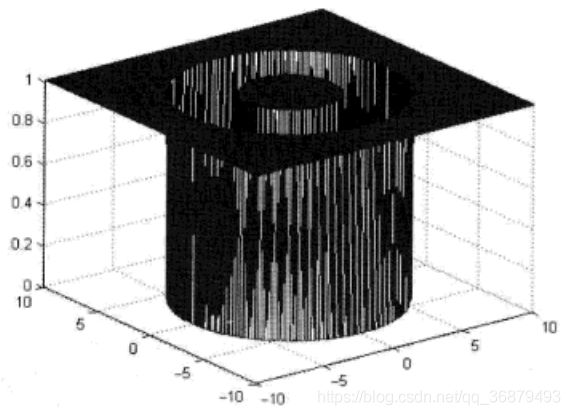
所谓 “带阻” 就是阻止频谱中某一频带范围的分量通过,其他频率成份则不受影响。常见的带阻滤波器有理想带阻滤波器和高斯带阻滤波器。
6.1.1、理想带阻滤波器
理想带阻滤波器的表达式为:
H ( u , v ) = { 0 , ∣ D − D 0 ∣ ≤ W 1 , ∣ D − D 0 ∣ > W H(u,v)=\begin{cases}0,|D-D_0|\leq W \\ 1,|D-D_0|>W \end{cases} H(u,v)={0,∣D−D0∣≤W1,∣D−D0∣>W
式中:D0 是阻塞频带中心频率到频率原点的距离;W 是阻塞频带宽度;D 是 (u,v) 点到频率原点的距离。
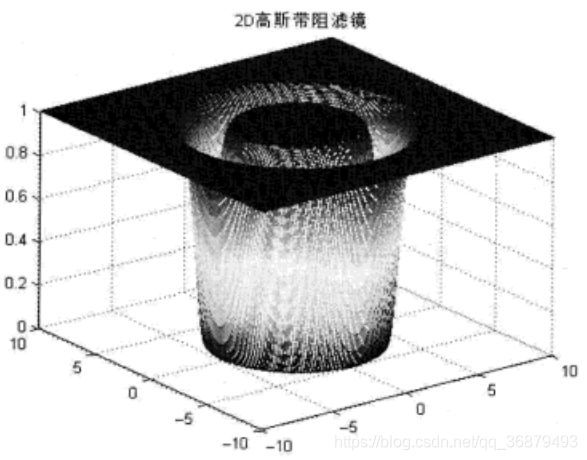
6.1.2、高斯带阻滤波器
H ( u , v ) = 1 − e − 1 2 [ D 2 ( u , v ) − D 0 2 D ( u , v ) W ] 2 H(u,v)=1-e^{-\frac{1}{2}[\frac{D^2(u,v)-D_0^2}{D(u,v)W}]^2} H(u,v)=1−e−21[D(u,v)WD2(u,v)−D02]2
式中:D0 是阻塞频带中心频率到频率原点的距离;W 是阻塞频带宽度;D 是 (u,v) 点到频率原点的距离。
6.1.3、高斯带阻滤波器的 Matlab 实现
编写了 imgaussfbrf 函数:
function ff = imgaussfbrf(I,freq,width)
% imgaussbrf函数 构造高斯带阻滤波器
% I参数 输入的灰度图像
% freq参数 截止频率
% width参数 阻带宽度
% 返回值 ff 与I等大的频域滤镜
[M,N] = size(I);
ff = ones(M,N);
for i = 1:M
for j = 1:N
ff(i,j) = 1 - exp(-0.5*((((i - M/2)^2 + (j - N / 2).^2) - freq^2) / (sqrt((i - M/2)^2 + (j - N / 2)^2) * width))^2); %gauss带阻滤波器公式
end
end
6.2、带阻滤波消除周期噪声
6.2.1、得到周期噪声图像
通常使用正弦平面波来描绘周期性噪声。
img = imread('lena.BMP');
[M,N] = size(img);
I = img;
for i = 1:M
for j = 1:N;
I(i,j) = I(i,j) + 20 * sin(20 * i) + 20 * sin(20 * j); %给原图像添加周期性噪声
end
end
figure;
subplot(3,2,1);
imshow(img);
title('原图');
subplot(3,2,2);
imshow(I);
title('added noise');
%得到频谱
f = fft2(img);
f = abs(fftshift(f)); %频谱
f = log(1 + f); %压缩频率范围
f1 = fft2(I);
f1 = abs(fftshift(f1)); %频谱
f1 = log(1 + f1); %压缩频率范围
subplot(3,2,3);
imshow(f,[]);
title('原图频谱');
subplot(3,2,4);
imshow(f1,[]);
title('added noise 频谱');
%带阻滤波
ff = imgaussfbrf(I,50,5); % 构造带阻滤波器,截止频率为50,阻带宽度为5
subplot(3,2,5);
imshow(ff,[]);
title('高斯带阻滤波器');
out = imfreqfilt(I,ff); % 带阻滤波
subplot(3,2,6);
imshow(out,[]);
title('带阻滤波结果');