机器学习实战——分类及性能测量完整案例（建议收藏慢慢品）

写在前面

参考书籍：Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

❤ 本文为机器学习实战学习笔记，主要内容为第三章分类，文中除了书中主要内容，还包含部分博主少量自己修改的部分，如果有什么需要改进的地方，可以在 评论区留言 ❤。

---

❤更多内容❤

机器学习实战——房价预测完整案例（建议收藏慢慢品）

---

1. 获取数据

本文使用的是 MNIST 数据集，这是一组由美国高中生和人口调查局员工手写的 70000 个数字的图片。每张图片都用其代表的数字标记。它被誉为机器学习领域的 “Hello World” 。我们可以直接通过 Scikit-Learn 来获取 MINST 数据集。

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
# 获取mnist的键值
mnist.keys()

dict_keys([‘data’, ‘target’, ‘frame’, ‘categories’, ‘feature_names’, ‘target_names’, ‘DESCR’, ‘details’, ‘url’])

---

Scikit-Learn 加载的数据集通常具有类似的字典结构，包括

• DESCR：描述数据集。
• data：包含一个数组，每个实例为一行，每个特征为一列。
• target：包含一个带有标记的数组。

# 获取特征与标签
X, y = mnist["data"], mnist["target"]
print(X.shape, y.shape)

(70000, 784) (70000,)

---

数据集共有 7 万张图片，每张图片有 784 个特征。图片为 28×28 像素，每个特征代表一个像素点的强度，从 0 （白色）—— 255 （黑色）。我们可以先用 Matplotlib 来显示一张图片看一下。

import matplotlib as mpl
import matplotlib.pyplot as plt
from pathlib import Path

current_path = Path.cwd()

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
# 显示灰色图
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
# 显示彩色图
# plt.imshow(some_digit_image)
plt.axis("off")

# 保存灰色图
plt.savefig(Path(current_path, "./images/some_digit_plot.png"), dpi=600)
# 保存彩色图
# plt.savefig(Path(current_path, "./images/some_digit_plot_colour.png"), dpi=600)
plt.show()

灰色图

彩色图

---

我们看一下它对应的标签。

y[0]

‘5’

标签的结果与图片相符。

---

此时的标签是字符，需要转为整数。

import numpy as np

y = y.astype(np.uint8)

5

---

在进行之后的步骤之前，需先创建一个测试集，将它与训练集分开。

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

---

2. 训练二元分类器

我们先尝试训练一个区分两个类别：5 和非 5 的二元分类器，首先创建目标向量。

y_train_5 = (y_train == 5)    # [ True False False ...  True False False]
y_test_5 = (y_test == 5)

---

接着挑选一个分类器进行训练。一个好的选择随机梯度下降（ SGD ）分类器，它的优势在于：能够有效处理非常大型的数据集，这是由于 SGD 独立处理训练实例，一次一个实例（这也使得 SGD 非常适合在线学习）。先创建一个 SGDClassifier 并在整个训练集上进行训练。

from sklearn.linear_model import SGDClassifier

# 构建分类器
sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
# 训练分类器
sgd_clf.fit(X_train, y_train_5)
# 预测
sgd_clf.predict([some_digit])

array([ True])

SGDClassifier 预测整个图像属于 5 ，结果正确，下面评估一下整个模型的性能。

---

3. 性能测量

3.1 交叉验证测量准确率

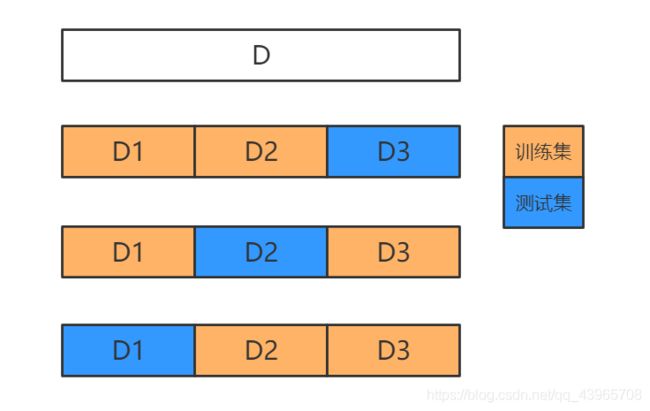
使用 Scikit-Learn 中的 cross_val_score() 函数来评估 SGDClassifier 模型，采用 K 折交叉验证法。这里使用 K=3 ，三个折叠，即将训练集分成 3 个折叠，每次留其中的 1 个折叠进行预测，剩余 2 个折叠用来训练，共重复 3 次。

from sklearn.model_selection import cross_val_score

# 交叉验证获取每次的模型准确率
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.95035, 0.96035, 0.9604 ])

---

3 次交叉验证的结果看上去都不错，超过 95%，但事实真的如此？下面构建一个只预测非 5的分类器，我们看一下它交叉验证的评估结果。

from sklearn.base import BaseEstimator

# 构建分类器
class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        pass
    def predict(self, X):
        # 返回全1的数组
        return np.zeros((len(X), 1), dtype=bool)

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.91125, 0.90855, 0.90915])

对于只预测非 5 的分类器，交叉验证的结果依旧很好，这说明训练集中大约只有 10% 的图片是数字 5。

---

我们看一下 y_train_5 中 非5 的比例是否在 90% 左右。

len(y_train_5[y_train_5==False]) / len(y_train_5)

0.90965

通过上面的结果，可以说明准确率往往无法成为分类器的首要性能指标，特别是在你处理不平衡的数据集时。

---

3.2 混淆矩阵

评估分类器性能的更好的方法是混淆矩阵。

混淆矩阵：统计A类别实例被分成B类别的次数

要计算混淆矩阵，需要先有一组预测才能将其与实际目标进行比较。当然可以通过测试集进行预测，但在目前阶段最好不要使用（测试集最好留到最后，在准备启动分类器时再使用）。我们可以使用 cross_val_predict() 函数来替代。

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
print(y_train_pred)
y_train_pred.shape

输出
[ True False False … True False False]
(60000,)

与 cross_val_score() 函数一样， cross_val_predict() 函数同样执行K折交叉验证，但返回的不是评估分数，而是每个折叠的预测。

---

现在可以使用 confusion_matrix() 函数来获取混淆矩阵，只需要给出 y_train_5 （目标类别）和 y_train_pred（预测类别）即可。

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

输出

---

在进行下面内容之前要确保你已经了解以下含义：

• TP（True Positive）：真 正类，模型预测样本为正类，实际也是正类。
• FP（False Positive）：假 正类， 模型预测样本为正类，实际上是负类。
• TN（True Negative）：真 负类，模型预测样本为负类，实际上也是负类。
• FN（True Negative）：假 负类，模型预测样本为负类，实际上是正类。

我们将上面结果以图的形式展示出来。

混淆矩阵中的行表示实际类别，列表示预测类别。图中我们可以得到以下信息：

• 在第一行表示所有实际类别是 非5 的图片中：
  • 53892 张被正确的分为 非5 类别（真负类 TN ）
  • 687 张被错误的分为 5 类别（假正类 FP）
• 在第一行表示所有实际类别是 5 的图片中：
  • 1891 张被错误的分为 非5 类别（假负类 FN ）
  • 3530 张被正确的分为 5 类别（真正类 TP ）

---

一个完美的分类器只有真正类和真负类，所以它的混淆矩阵只会在其对角线（左上——右下）上有非零值。如下所示：

 # 直接以实际标签作为预测结果，来塑造一个完美的分类结果
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions)

输出

---

3.3 精度和召回率

混淆矩阵确实能够提供大量的信息，但如果希望指标更简洁一些，分类器的精度可能更加适合。

精度：正类预测的准确率
$$精度=\frac{TP}{TP+FP}$$
TP 是真正类的数量， FP 是假正类的数量。

---

精度通常和召回率一起使用。

召回率：正确检测到的正类实例的比率
$$召回率=\frac{TP}{TP+FN}$$
TP 是真正类的数量， FN 是假负类的数量。

---

在 Scikit-Learn 中可以使用 precision_score ， recall_score 来计算精度和召回率。

from sklearn.metrics import precision_score, recall_score

print('精度：', precision_score(y_train_5, y_train_pred))
print('召回率：', recall_score(y_train_5, y_train_pred))

输出
精度： 0.8370879772350012
召回率： 0.6511713705958311

---

也可以使用混淆矩阵进行计算。结果一样。

cm = confusion_matrix(y_train_5, y_train_pred)

print('精度：', cm[1, 1] / (cm[0, 1] + cm[1, 1]))
print('召回率：', cm[1, 1] / (cm[1, 0] + cm[1, 1]))

输出
精度： 0.8370879772350012
召回率： 0.6511713705958311

---

根据精度和召回率的结果来看，它不再像准确率那么高了。当它预测一张图片为 5 时，他只有 83.7% 的概率是准确的，在整个测试集中也只有 65.1% 的 5 被正确检测出来。

---

3.4 $F_1$分数

我们可以将精度和召回率组合成一个指标，称为$F_1$分数。

$F_1$分数：精度和召回率的谐波平均值
$$F_1=\frac{2}{\frac{1}{精度}+\frac{1}{召回率}}=\frac{TP}{TP+\frac{FN+FP}{2}}$$
它会给予精度和召回率中的低值更高的权重。只有当精度和召回率都很高时，$F_1$分数才高。

---

在 Scikit-Learn 中可以使用 f1_score 来计算$F_1$分数。

from sklearn.metrics import f1_score

f1_score(y_train_5, y_train_pred)
# cm[1, 1] / (cm[1, 1] + (cm[1, 0] + cm[0, 1]) / 2)

0.7325171197343846

---

$F_1$分数对那些具有相近精度和召回率的分类器更有利。在实际情况下，我们有时更关注的是精度，如青少年视频筛选，我们要尽量保证筛选出来的都是符合要求的，而对于财务造假，我们就需要更关注召回率。鱼和熊掌不可兼得，精度和召回率同样也是。

---

3.5 精度/召回率权衡

要理解这个权衡过程，首先要知道 SGDClassifier 如何进行分类的。对于数据集中的每一个实例，它会基于决策函数计算出一个分值，如果该值大于设定的阈值，则将该实例判为正类，否则便将其判为负类。
图中显示从左边最低分到右边最高分的几个数字，假设当前决策阈值位于①箭头的位置，在阈值的右边有四个 5（真正类）和一个 6 （假正类），因此精度为 80% 。在五个 5 中，只预测出了 4 个，召回率为 80% 。
现在提高阈值，以②箭头的位置作为决策阈值，此时，精度变为 100% ，召回率变为 60% 。

---

Scikit-Learn 不允许直接设置阈值，但可以使用 decision_function() 方法访问它用于预测的决策分数，该方法返回每个实例的分数，根据这些分数就可以使用任意阈值进行预测。下面先获取 3 个实例的决策分数。

y_scores = sgd_clf.decision_function(X[:3])
y_scores

array([ 2164.22030239, -5897.37359354, -13489.14805779])

---

使用 SGDClassifier 默认的决策阈值 0 ，来得到分类结果。

threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([ True, False, False])

---

现在提升阈值看看是否会改变分类结果。

threshold = 3000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([False, False, False])

结果发生了改变，这证明提高阈值确实可以降低召回率。

---

那我们如何在众多的实例中选择恰当的决策阈值？
首先使用 cross_val_predict() 函数获取训练集中所有所有实例的决策分数（修改 method 参数）。

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")
y_scores.shape

(60000,)

---

使用 precision_recall_curve() 函数来计算所有可能的阈值的精度和召回率。

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

---

最后使用 Matplotlib 绘制精度和召回率相对于阈值的函数图。

# 显示中文
plt.rcParams['font.family'] = 'SimHei'
# 显示中文负号
plt.rcParams['axes.unicode_minus'] = False

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
	# 绘制精度曲线
    plt.plot(thresholds, precisions[:-1], "b--", label="精度", linewidth=2)
    # 绘制召回率曲线
    plt.plot(thresholds, recalls[:-1], "g-", label="召回率", linewidth=2)
    # 设置图例的位置与大小
    plt.legend(loc="center right", fontsize=16)
    # 设置x轴的信息
    plt.xlabel("Threshold", fontsize=16)
    # 显示网格
    plt.grid(True)
    # 指定坐标轴的范围
    plt.axis([-50000, 50000, 0, 1])

# 设置图像的大小
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
# 保存图片
plt.savefig(Path(current_path, "./images/precision_recall_vs_threshold_plot.png"), dpi=600)
plt.show()

注意： 在精度曲线上，上端有部分是崎岖的，这是由于当你提高阈值时，精度有时也可能会下降。

---

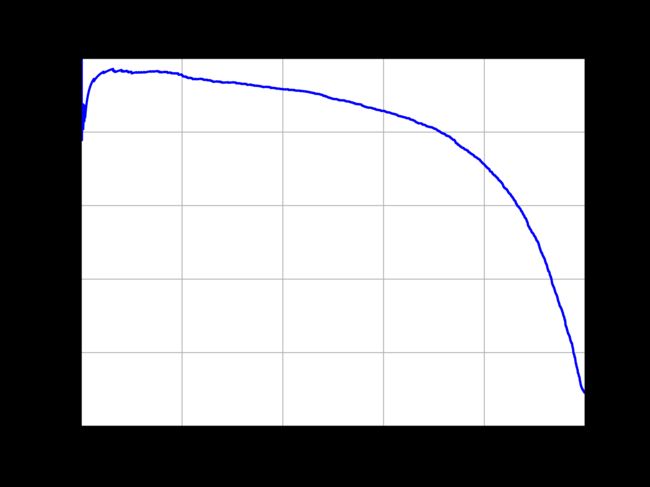
另一种找到好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图。

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("召回率", fontsize=16)
    plt.ylabel("精度", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

# 设置绘制图像大小
plt.figure(figsize=(8, 6))
# 图像绘制
plot_precision_vs_recall(precisions, recalls)
# 保存图片
plt.savefig(Path(current_path, "./images/precision_vs_recall_plot.png"), dpi=600)
plt.show()

从图中可以看到，从80%召回率往右，精度开始极度下降。你可能会尽量在这个陡降之前选择一个精度/召回率权衡，这要根据项目的实际情况来定。

---

假如你需要将精度设为 90% ，那么需要知道能提供 90% 精度的最低阈值。可以用 np.argmax() 函数来获取。

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
threshold_90_precision

3370.0194991439557

---

获得预测结果。

y_train_pred_90 = (y_scores >= threshold_90_precision)
print('精度：', precision_score(y_train_5, y_train_pred_90))
print('召回率：', recall_score(y_train_5, y_train_pred_90))

输出
精度： 0.9000345901072293
召回率： 0.4799852425751706

这样就得到了一个接近 90% 精度的分类器了！

---

3.6 ROC曲线

还有一种经常与二元分类器一起使用的工具，叫做受试者工作特征曲线（ ROC ）。它绘制的是真正类率（ TPR 召回率）与假正类率（ FPR ）的关系。

• 真正类率（ TPR ）：预测为正例，且实际为正例的样本占所有正例样本（真实结果为正样本）的比例。
• 假正类率（ FPR ）：预测为正例，但实际为负例的样本占所有负例样本（真实结果为负样本）的比例。

$$TPR=\frac{TP}{TP+FN}$$
TP 是真正类的数量， FN 是假负类的数量。

$$FPR=\frac{FP}{FP+TN}$$
TP 是假正类的数量， FN 是真负类的数量。

---

要绘制 ROC 曲线，首先需要使用 roc_curve() 函数计算多种阈值的 TPR 和 FPR ：

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

---

使用 Matplotlib 绘制 FPR 对 TPR 的曲线。

def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--') # 绘制虚线对角线
    plt.axis([0, 1, 0, 1])
    plt.xlabel('假正类率(FPR)', fontsize=16)
    plt.ylabel('真正类率(TPR)', fontsize=16)
    plt.grid(True)

# 设置绘制图像大小
plt.figure(figsize=(8, 6))
# 绘制FPR对TPR的曲线
plot_roc_curve(fpr, tpr)
# 保存图片
plt.savefig(Path(current_path, "./images/roc_curve_plot.png"), dpi=600)
plt.show()

召回率（ TPR ）越高，分类器产生的假正类（ FP ）就越多。虚线表示纯随机分类器的 ROC 曲线，一个好的分类器应该离这条线越远越好（接近左上角）。

---

一种常用的比较分类器 ROC 曲线的方法就是测量曲线下的面积（ AUC ）。完美的分类器 ROC AUC 等于 1 ，而纯随机分类器 ROC AUC 等于 0.5 。可以使用 Scikit-Learn 中的 roc_auc_score 来计算 ROC AUC 的值。

from sklearn.metrics import roc_auc_score

roc_auc_score(y_train_5, y_scores)

0.9604938554008616

---

ROC曲线与PR（精度 / 召回率）曲线的选择
当正类非常少时或你更关注假正类而不是假负类时，应该选择 PR 曲线，反之则选择 ROC 曲线。

---

现在我们来训练一个 RandomForestClassifier 分类器，并比较它和 SGDClassifier 分类器的 ROC 曲线和 ROC AUC 分数。 RandomForestClassifier 类没有 decision_function() 方法，它由 dict_proba() 方法。该方法会返回一个数组，其中每行代表一个实例，每列代表一个类别，意思是某个给定实例属于某个给定类别的概率。

from sklearn.ensemble import RandomForestClassifier

# 创建一个随机森林分类器
forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
# 使用交叉验证获得类别概率的平均值
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
y_probas_forest

输出

根据结果可以看到，数组中包含该实例属于 非5 或 5 的概率值， shape 为 (60000, 2) 。

---

roc_curve() 函数需要标签和分数，我们直接使用正类的概率最为分数值。

y_scores_forest = y_probas_forest[:, 1]    # score取属于正类的概率
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)

绘制 ROC 曲线。

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")

plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
plt.savefig(Path(current_path, "./images/roc_curve_comparison_plot.png"), dpi=600)
plt.show()

RandomForestClassifier 的 ROC 曲线看起来比 SGDClassifier 好的多，它离左上角更近，因此它的 ROC AUC 分数也高得多。下面也看看精度和召回率的分数。

# ROC AUC分数
print('ROC AUC分数: ', roc_auc_score(y_train_5, y_scores_forest))

# 交叉验证获取平均预测结果
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
# 精度
precision_score('精度: ', y_train_5, y_train_pred_forest)
# 召回率
recall_score('召回率: ', y_train_5, y_train_pred_forest)

输出
ROC AUC分数: 0.9983436731328145
精度: 0.9905083315756169
召回率: 0.8662608374838591

看起来结果也不错，现在对二元分类器已经有了一个基本的了解，知道了如何使用合适的指标利用交叉验证来对分类器进行评估，如何选择满足需求的 精度/召回 权衡，以及如何使用 ROC 曲线和 ROC AUC 分数比较多个模型，接下来尝试一下多类分类器。

---

4. 多类分类器

多类分类器可以区分两个以上的类。有一些算法（如 随机森林分类器 或 朴素贝叶斯分类器 ）可以直接处理多个类。也有一些严格的二元分类器（如 支持向量机分类器 或 线性分类器 ）。但是，有多种方法可以让你用几个二元分类器实现多类分类的目的。

如现在要创建一个系统将数字图片分为 10 类（ 0-9 ）

• 一种方法是训练 10 个二元分类器，每个数字一个，当某张图片进行分类时，获取每个分类器的决策分数，将得分最高的分类器分类的结果作为它的类别。这叫做一对剩余策略（ OvR ）。
• 另一种方法是对每一个数字训练一个二元分类：一个用来区别 0与 1 ，一个用来区别 0 与 2 ，一个用来区别1 与 2 ，依次类推，这叫做一对一策略（ OvO ）。如果存在 N 个类别，那么训练器的个数就是：
  $$\frac{N\times (N-1)}{2}$$
  当某张图片进行分类时，要运行所有的分类器来对图片进行分类，看分到哪个类的次数最多就将其分到那个类。 OvO 的主要优点就是：每个分类器只需要用到部分训练集对其所区分的两个类进行训练。

有些算法（如 支持向量机分类器 ）在数据规模扩大时表现非常糟糕，对于这类算法， OvO 是一个较好的选择，因为在较小训练集上分别训练多个分类器比在大型数据集上训练少量分类器要快得多。但对于大多数二元分类器来说， OvR 策略还是更好的选择。

---

Scikit-Learn 可以检测到你尝试使用二元分类器进行多分类任务，它会根据情况自动运行 OvR 或 OvO 。我们先试试 SVM 分类器：

from sklearn.svm import SVC

# 创建分类器
svm_clf = SVC(gamma="auto", random_state=42)
# 训练分类器
svm_clf.fit(X_train[:1000], y_train[:1000])
# 对X_train前三个实例进行分类
svm_clf.predict(X_train[:3])

array([5, 0, 4], dtype=uint8)

上面代码使用包含类别 0-9 的数据集对 SVC 进行训练，然后对测试集进行预测，在内部， Scikit-Learn 实际上训练了 45 个分类器，获得它们对图片的决策分数，选择分数最高的类。我们可以用 decision_function() 方法验证一下，该方法会获得 10 个分数，每个类 1 个。

---

some_digit_scores = svm_clf.decision_function(X_train[:3])
some_digit_scores

输出

最高的分数分别是分类5 ，分类0 ，分类4 。

---

在训练分类器时，目标类的列表会存储在 classes_ 属性中，按值的大小进行排序。

svm_clf.classes_

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)

---

如果要强制 Scikit-Learn 使用一对一或一对多策略，可以使用 OneVsOneClassifier 或 OneVsRestClassifier 类。只需要创建一个实例，然后将分类器传给其构造函数即可。例如下面使用 OvR 策略，基于 SVC 创建一个多类分类器。

from sklearn.multiclass import OneVsRestClassifier

# 将SVC分类器传给构造函数
ovr_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))
# 训练分类器
ovr_clf.fit(X_train[:1000], y_train[:1000])
# 分类
ovr_clf.predict(X_train[:3])

array([5, 0, 4], dtype=uint8)

查看此时分类器的数量

len(ovr_clf.estimators_)

10

---

5. 误差分析

现在假设已经找到了一个有潜力的模型，希望能够找到一些方法对其进行改进，方法之一就是分析其错误类型。
首先看看混淆矩阵，使用 cross_val_predict() 函数进行预测，然后调用 confusion_matrix() 函数：

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
# 标准化
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
# 交叉验证
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
# 计算混淆矩阵
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx

输出

---

由于是多分类，数组为 10 × 10 ，使用 Matplotlib 的 matshow() 函数来查看混淆矩阵的图像。

plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.savefig(Path(current_path, "./images/confusion_matrix_plot.png"), dpi=600)
plt.show()

混淆矩阵中，每行表示每个实际类别，每列表示每个预测类别。混淆矩阵中大多数图片都在对角线上，这说明它们被正确的分类。但数字 5 的颜色比较暗，可能是因为测试集中的数字 5 的图片较少，也可能是因为该分类的分类效果不太好。

---

由于目前混淆矩阵的值是错误数量的绝对值，它会受到各分类图片数量的影响。我们需要将混淆矩阵中的每一个值除以相应类中的图片数量，这样比较的就是错误率了。为了凸显错误的种类，我们将对角线的值填充为0（因为它所占的比例很大，不将它填充0，其他的值颜色就难以区分开），重新绘制结果。

row_sums = conf_mx.sum(axis=1, keepdims=True)
# 混淆矩阵的每个值 / 单个实际类别总数量
norm_conf_mx = conf_mx / row_sums
# 用0填充主对角线
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.savefig(Path(current_path, "./images/confusion_matrix_errors_plot.png"), dpi=600)
plt.show()

现在能够清晰的看到分类器产生的错误种类了，第 8 列非常亮，说明许多实际类别不是 8 的被错误的分类为数字 8 ，但根据第 8 行的颜色，准确分类为 8 的效果也还不错。对于这种分类错误，我们可以尝试和收集更多看起来像数字 8 的训练数据，以便分类器能够通过特征将它与其他数字区分开。或者对图片进行预处理（使用 Scikit-Image 、 Pillow 或 Opencv ）让闭环（ 8 有两个）更加突出等。同时上图中的数字 3 和数字 5 经常混淆（红框圈出）。

---

6. 多标签分类

在之前，每个实例都只会被分在一个类别里面。而在某些情况下，我们希望分类器给每个实例输出多个类，如人脸识别时，在一张图片上识别出多个人，这时应该为每个识别出的人都附一个标签。下面看一个简单的例子。创建一个 y_multilabel 数组，其中包含两个数字图片的目标标签：第一个表示数字是$⩾7$，第二个表示是否是奇数。

from sklearn.neighbors import KNeighborsClassifier

# 将y_train中大于7的值标为True，其余False
y_train_large = (y_train >= 7)
print('y_train_large:\n', y_train_large)
# 将y_train中奇数值标为True，其余False
y_train_odd = (y_train % 2 == 1)
print('y_train_odd:\n', y_train_odd)
# 将y_train_large, y_train_odd按行进行连接，合并前后的行数不变
y_multilabel = np.c_[y_train_large, y_train_odd]
print('y_multilabel:\n', y_multilabel)

输出

创建 KNeighborsClassifier() 实例，用上面的 y_multilabel 数组进行训练，并进行预测。

# 输出测试标签实际类别
print('y_train[:3]: ', y_train[:3])

# 创建KNeighborsClassifier()实例
knn_clf = KNeighborsClassifier()
# 训练分类器
knn_clf.fit(X_train, y_multilabel)
# 预测
knn_clf.predict(X_train[:3])

输出

可以看到，预测结果都是正确的。三个测试实例的值都小于 7 ，并且只有 5 是奇数。

注：这里假设所有标签都同等重要，但实际情况可能不是这样，比如上面例子中的奇数的数量可能会$⩾7$的标签的数量要多，这时可以给每个标签设置一个等于自身的权重（也就是具有该目标标签的实例的数量）。为了达到这个目的，我们只需要在上面的代码中设置 average=“weighted” 。

---

7. 多输出分类

最后一种分类任务称为多输出-多类分类，简单的来说，它是多标签分类的泛化，其标签也可以是多类的。
下面构建一个系统用于去除图片中的噪音。给它输入一张有噪音的图片，它会输出一张“干净”的图片。这个分类器的输出是多个标签（一个像素点一个标签），每个标签可以有多个值（像素强度范围为0-255）。所以它是一个多标签多类分类的分类器。

---

首先创建训练集和测试集：

# 创建训练集噪音数组
noise = np.random.randint(0, 100, (len(X_train), 784))   # (60000, 784)
# 在训练集中加入噪音
X_train_mod = X_train + noise                            # (60000, 784)
# 创建测试集噪音数组
noise = np.random.randint(0, 100, (len(X_test), 784))    # (10000, 784)
# 在测试集中加入噪音
X_test_mod = X_test + noise                              # (10000, 784)

# 将没加入噪音的训练图片作为训练集的标签
y_train_mod = X_train                                    # (60000, 784)
# 将没加入噪音的测试图片作为测试集的标签
y_test_mod = X_test                                      # (10000, 784)

---

显示添加噪音前后的图片，进行对比。

def plot_digit(data):
    # 更改data形状
    image = data.reshape(28, 28)
    # 显示灰度图
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    # 不显示坐标轴
    plt.axis("off")
    
some_index = 0
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
plt.savefig(Path(current_path, "./images/noisy_digit_example_plot.png"), dpi=600)
plt.show()

---

通过训练分类器，清洗图片。

# 训练分类器
knn_clf.fit(X_train_mod, y_train_mod)
# 获得清洗结果
clean_digit = knn_clf.predict([X_test_mod[some_index]])
# 绘制清洗后的数字
plot_digit(clean_digit)
# 保存图片
plt.savefig(Path(current_path, "./images/cleaned_digit_example_plot.png"), dpi=600)

这个结果已经十分接近上面未添加噪音的原图了。

---

分类之旅到此结束！！！

都看到这了，看在博主这么辛苦的份上，❤ 点个赞再走吧！！！❤


后续会继续分享机器学习的学习笔记，如果感兴趣的话可以点个关注不迷路。


如果需要完整代码（.ipynb）练练手的话，可以在评论区留下邮箱，看见必发。