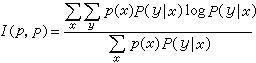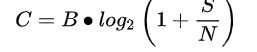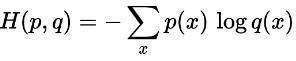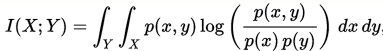信息论在人工智能方面应用
香农三大定理与新社会人工智能发展的羁绊:
克劳德·艾尔伍德·香农(Claude Elwood Shannon,1916年4月30日-2001年2月24日)是美国数学家、信息论的创始人。1936年获得密歇根大学学士学位 。1940年在麻省理工学院获得硕士和博士学位,1941年进入贝尔实验室工作。
香农提出了信息熵的概念,为信息论和数字通信奠定了基础。
主要论文有:1938年的硕士论文《A Symbolic Analysis of Relay and Switching Circuits》,1948年的《通讯的数学原理》和1949年的《噪声下的通信》。
信息论概述
信息论是运用概率论与数理统计的方法研究信息传输和信息处理系统中一般规律的新兴学科。核心问题是信息传输的有效性和可靠性以及两者间的关系。
信息论作为一门科学理论,发端于通信工程。它具有广义和狭义两个概念:
狭义信息论是应用统计方法研究通讯系统中信息传递和信息处理的共同规律的科学,即研究概率性语法信息的科学;
广义信息论是应用数学和其他有关科学方法研究一切现实系统中信息传递和处理、信息识别和利用的共同规律的科学,即研究语法信息、语义信息和语用信息的科学。
信息是事物及其属性标识的集合
信息就是信息,信息是物质、能量、信息及其属性的标示。
信息是确定性的增加。即肯定性的确认。
信息论形成和发展
人们对于信息的认识和利用,可以追溯到古代的通讯实践。中国古代的“烽燧相望”和古罗马地中海诸城市的“悬灯为号”,可以说是传递信息的原始方式。随着社会生产的发展,科学技术的进步,人们对传递信息的要求急剧增加。到了20世纪20年代,如何提高传递信息的能力和可靠性已成为普遍重视的课题。美国科学家N.奈奎斯特、德国K.屈普夫米勒、前苏联A.H.科尔莫戈罗夫和英国R.A.赛希尔等人,从不同角度研究信息,为建立信息论作出很大贡献。1948年,美国数学家C.E.香农(被称为是“信息论之父”)出版《通信的数学理论》,1949年发表《噪声中的通信》,从而奠定了信息论的基础。20世纪70年代以后,随着数学计算机的广泛应用和社会信息化的迅速发展,信息论正逐渐突破香农狭义信息论的范围,发展为一门不仅研究语法信息,而且研究语义信息和语用信息的科学。它的建立是人类认识的一个飞跃。世界上各种事物都是充满矛盾不断发展的,物质的运动主要是靠内部矛盾运动所产生的能量,而事物之间的普遍联系则靠的是信息。信息是关于事物的运动状态和规律,而信息论的产生与发展过程,就是立足于这个基本性质。信息论迅速渗透到各个不同学科领域,但还不够完善。为了适应科学技术发展的需要,迎接信息化社会的到来,一门新的科学正在迅速兴起,这就是广义信息论,或者叫做信息科学。信息科学是由信息论、控制论、计算机、人工智能和系统论等相互渗透、相互结合而形成的一门新兴综合性学科。信息科学登上现代科技舞台,与能量科学、材料科学鼎足而立 ,将为科学技术的发展作出贡献。
信息论的应用
信息论的意义和应用范围已超出通信的领域。自然界和社会中有许多现象和问题,如生物神经的感知系统、遗传信息的传递等,均与信息论中研究的信息传输和信息处理系统相类似。因此信息论的思想对许多学科如物理学、生物学、遗传学、控制论、计算机科学、数理统计学、语言学、心理学、教育学、经济管理、保密学研究等都有一定的影响和作用。另一方面,由于借助负熵定义的信息量只能反映符号出现的概率分布(不肯定性),不能反映信息的语义和语用层次。一篇重要的报告和一篇胡说乱道的文章可以具有同样的信息,这显然不符合常识。因此现阶段信息论的应用又有很大的局限性。把信息的度量推广到适合于语义信息和语用信息的情况,曾经做过许多尝试。但至今还没有显著的进展。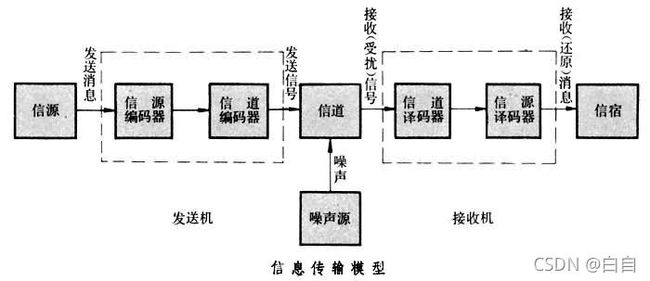
香农第一定理(可变长无失真信源编码定理)
设离散无记忆信源X包含N个符号{x1,x2,…,xi,..,xN},信源发出K重符号序列,则此信源可发出N^k个不同的符号序列消息,其中第j个符号序列消息的出现概率为PKj,其信源编码后所得的二进制代码组长度为Bj,代码组的平均长度B为B=PK1B1+PK2B2+…+PKN^kBN^k当K趋于无限大时,B和信息量H(X)之间的关系为B/k=H(X)(K趋近无穷)
香农第一定理又称为无失真信源编码定理或变长码信源编码定理。
香农第一定理的意义:将原始信源符号转化为新的码符号,使码符号尽量服从等概分布,从而每个码符号所携带的信息量达到最大,进而可以用尽量少的码符号传输信源信息。
香农第一定律讲的是,对于信源发出的所有信息涉及一个编码,一定存在一种编码方式,使得编码的平均长度无限接近与它的信息熵
举例说明:比如对汉字编码,有些字用的多,有些字用的少,因此可以把常用字的编码做的短些,生僻字的编码做的长些,但是无论怎么做,编码的平均长度一定会超过汉字的不确定性,即他们的信息熵。
这是香农第一定律的第一层意思。
它的第二层意思是一定存在一种(最优)编码方法,使得每个汉字的平均编码长度可以非常接近它的不确定性(信息熵)。至于怎么做,霍夫曼给出了一个非常简单的方法--只要把最短的编码分配给最常见的汉字即可。这种编码方法具有通用性,又称霍夫曼编码。
在计算机数据处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
可以认为是对香农第一定律的补充。
香农第二定理(有噪信道编码定理)
当信道的信息传输率不超过信道容量时,采用合适的信道编码方法可以实现任意高的传输可靠性,但若信息传输率超过了信道容量,就不可能实现可靠的传输。设某信道有r个输入符号,s个输出符号,信道容量为C,当信道的信息传输率R 注:B为信道带宽;S/N为信噪比,通常用分贝(dB)表示。 理解: 1.信息通道的传输率R,是无论如何都无法超越信道容量C的,即R≤C; 2.总能找到一种编码方式,使得传输率R无限接近信道容量C,同时保证传输不出现任何错误; 3.如果谁要试图超越信道容量传输信息,无论你怎样编码,出错的概率都是100%。 以浏览网页为例子来说明。 服务器端把信息发送到客户端(浏览器),服务器端不会等客户端发送确认接收到的信息后才会继续发送,而是不断的发送消息,如果网络带宽只有56K(电话拨号上网),那么由于客户端没有及时迅速的反馈确认信息给服务器端,因此服务器端会把先前发过的信息重新再发送,而新的消息也在不断的发,但发的越多,接收不到确认的信息就越多,而且还是多次的重发,形成正反馈回路直至把信道堵死。这就是为什么以前使用电话拨号,看似很少内容的网页,总是打开不了或者打开不完整的原因。 保真度准则下的信源编码定理,或称有损信源编码定理。 只要码长足够长,总可以找到一种信源编码,使编码后的信息传输率略大于率失真函数,而码的平均失真度不大于给定的允许失真度,即D'<=D.设R(D)为一离散无记忆信源的信息率失真函数,并且选定有限的失真函数,对于任意允许平均失真度D>=0,和任意小的a>0,以及任意足够长的码长N,则一定存在一种信源编码W,其码字个数为M<=EXP{N[R(D)+a]},而编码后码的平均失真度D'(W)<=D+a。 第三定理有损信源编码定理解决了在允许一定失真的情况下的信源编码问题,比如jpeg图像编码,mp3音频编码,都是有损的编码,其都是在香农第三定理的界之下得出的;、 音频信号能进行压缩的依据是音频压缩技术。 音频压缩技术指的是对原始数字音频信号流(PCM编码)运用适当的数字信号处理技术,在不损失有用信息量,或所引入损失可忽略的条件下,降低(压缩)其码率,也称为压缩编码。它必须具有相应的逆变换,称为解压缩或解码。音频信号在通过一个编解码系统后可能引入大量的噪声和一定的失真。 在音频压缩领域,有两种压缩方式,分别是有损压缩和无损压缩。常见到的MP3、WMA、OGG被称为有损压缩,有损压缩顾名思义就是降低音频采样频率与比特率,输出的音频文件会比原文件小。另一种音频压缩被称为无损压缩,也就是所要说的主题内容。无损压缩能够在100%保存原文件的所有数据的前提下,将音频文件的体积压缩的更小。 直观来说熵就是表示事情不确定性的因素度量,熵越大不确定性就越大,而不确定性越大,带来的信息则越多。但是确定的东西,带来的不确定性很小,信息也很少,所以熵很低。熵=不确定性=信息量。他们三个成正比例。 例如太阳在东方升起,熵就为0。一枚质地均匀的硬币,出现正反面,熵就为1。 公式 设X为离散随机变量,概率分布: P ( X = xi ) = pi, i = 1,2,3,…,n 则随机变量X的熵为: H(p) = -∑ pi * log pi 由上式可以得出,太阳在东方升起、硬币正反面的熵运算。 信息增益字面理解,信息增加后对最后的目标结果有益处。也就是说通过选择合适的X特征作为判断信息,让Y的不确定性减少的程度越大,则选择出的X越好。而条件熵H(Y|X)表达就是给定X后,Y的不确定性是多少。 H ( Y | X ) = -∑ pi * H ( Y | X = xi ) 这里 pi = P( X = xi ) ,i = 1,2,…,n 熵和条件熵中的概率如果通过估计得到,例如极大似然估计,则熵和条件熵将会,变名字经验熵和经验条件熵。 交叉熵被设置为模型的损失函数,表示的两个概率分布的相似程度,交叉熵越小代表预测的越接近真实。q(x)代表的是预测概率,p(x)代表的是真实概率。 二分类问题交叉熵公式 L=−[ylog y^+(1−y)log (1−y^)] y^代表预测的正例概率。y代表真实标签。模型可以是逻辑回归或者是神经网络,输出值映射成概率值需要sigmoid函数。 信息增益直观来说就是当给了你一条信息X,这条信息对你理解另一条信息Y有没有帮助,如果有帮助,则会使你对信息Y的理解加深,不理解的信息减少。则信息增益就等于Y的熵减给定X后Y的熵。公式如下: IG(Y|X) = H(Y)-H(Y|X) 信息增益作为决策树模型中的核心算法,是决策树模型中非叶子节点选择特征的重要评判标准,简单说一下决策树,决策树模型作为基于实例的模型,主要是叶节点(目标值或者目标类别),非叶节点是用于判断实例的特征属性。之后将依据信息论详细介绍决策树模型。 概率中两个随机变量的互信息是描述两个变量之间依赖性的度量。它也决定着两个变量的联合概率密度P(XY)与各自边际概率 P(X)和P(Y)乘积的相似程度。我们可以从概率学的知识了解到,如果X和Y之间相互独立,P(X)P(Y) = P(XY)。和相关系数不同,它不仅能获得线性关系,还可以获得非线性关系。互信息公式如下: 下图为连续型随机变量互信息的公式: p(x,y) 当前是 X 和 Y 的联合概率密度函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。 直观来说,互信息就是度量当已知一个信息,会对另一个信息的不确定性减少的程度,如果XY相互独立,则X不会减少Y的不确定性,互信息为0。所以互信息是非负的。 信源是产生消息(包括消息序列)的源。消息通常是符号序列或时间函数。例如电报系统中的消息是由文字、符号、数字组成的报文(符号序列),称为离散消息。电话系统中的消息是语声波形(时间函数),称为连续消息。消息取值服从一定的统计规律。因此,信源的数学模型是一个在信源符号集中取值的随机变量序列或随机过程。信源编码器将消息变换为一个数字序列(通常为二进制数字序列)。在离散情形,若信源产生M个可能消息,它们出现的概率分别为 信道是传输信息的媒质或通道,如架空明线、同轴电缆、射频波束、光导纤维等。有时为研究方便将发送端和接收端的一部分如调制解调器也划归信道。信息论把信息传送过程中受各种干扰的影响都归入信道中考虑。根据干扰的统计特性,信道有多种模型。最简单的是离散无记忆恒参信道,它可以用信道入口符号集X、出口符号集Y和一组条件概率P(y|x)(x∈X,y∈Y)来描述。若信道输入信号x=(x1,x2,…,xN),则相应的输出(受扰)信号y=(y1,y2,…,yN)出现的概率为 称为交互信息;C 称为信道容量,是信道的重要参数。香农第三定理(保失真度准则下的有失真信源编码定理)
基础信息论
1.熵
2.条件熵
3.交叉熵损失函数
4.信息增益
5.互信息(Mutual Information)
信源编码
![]() ,每个消息由N个信源符号组成,便可取信源编码与数字序列一一对应。第i个消息对应的数字序列长(数字个数)为li,li相等的称等长编码,否则称变长编码。定义
,每个消息由N个信源符号组成,便可取信源编码与数字序列一一对应。第i个消息对应的数字序列长(数字个数)为li,li相等的称等长编码,否则称变长编码。定义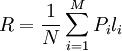 为编码速率,它表征平均每个信源符号要用多少个数字来表示。若取信源译码器为信源编码器的逆变换器,则在无噪信道(信源编码器的输出即为信源译码器的输入) 情况下,消息可以正确无误地传送。这时信源编码问题是要找出最小的速率R及其相应的编码。已经证明,对于相当广泛的信源类,当N可以任意大时这个最小极限速率
为编码速率,它表征平均每个信源符号要用多少个数字来表示。若取信源译码器为信源编码器的逆变换器,则在无噪信道(信源编码器的输出即为信源译码器的输入) 情况下,消息可以正确无误地传送。这时信源编码问题是要找出最小的速率R及其相应的编码。已经证明,对于相当广泛的信源类,当N可以任意大时这个最小极限速率![]() 称为信源的熵率,是信源的一个重要参数。对于固定的N,最优编码就是赫夫曼编码。在连续消息的情形,信息编码器不可能使消息与数字序列一一对应,因此译码也不是编码的逆变换。通常的方法是先对连续消息进行采样和量化,变为离散消息,再将离散消息变换为数字序列。信源译码器先将数字序列逆变换为离散消息,再用内插法求得连续消息。这样一来,即使在无噪信道的情况下,发送消息与接收消息之间也会产生误差,称为消息失真。可以用一个非负函数d(u,v)来度量消息 u,v之间的失真大小。这时信源编码问题是在保证平均失真不超过给定允许极限D 的条件下找出最小速率R 及其相应编码。求解这一问题导致熵推广到失真率函数,信源编码的失真率理论因而得到发展。
称为信源的熵率,是信源的一个重要参数。对于固定的N,最优编码就是赫夫曼编码。在连续消息的情形,信息编码器不可能使消息与数字序列一一对应,因此译码也不是编码的逆变换。通常的方法是先对连续消息进行采样和量化,变为离散消息,再将离散消息变换为数字序列。信源译码器先将数字序列逆变换为离散消息,再用内插法求得连续消息。这样一来,即使在无噪信道的情况下,发送消息与接收消息之间也会产生误差,称为消息失真。可以用一个非负函数d(u,v)来度量消息 u,v之间的失真大小。这时信源编码问题是在保证平均失真不超过给定允许极限D 的条件下找出最小速率R 及其相应编码。求解这一问题导致熵推广到失真率函数,信源编码的失真率理论因而得到发展。
信道编码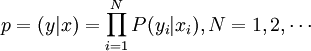 信道编码器将数字序列每K个一组变换为字长N 的信号(码字),称为分组编码。若数字和信道符号都是二进制的(可用0,1表示),则R=K/N 定义为编码速率,它表明每个信道符号表示多少个数字。N-K 称为编码冗余度。信道编码(纠错编码)的基本思想就是增加冗余度以提高可靠性。更确切地说,信道译码器可以利用编码冗余度将受扰信号变换为正确的发送数字序列。重复编码乃一简例。信道编码器将输入数字重复三次, 如将01011变换为000111000111111。信道译码器可用门限译码,即先将输入译码器的信道符号每三个一组地相加,再将结果逐个与阈值 2比较,小于阈值2的译为0,否则译为1。这样若受扰信号010110100011011虽然错了 5个符号,但译码仍为01011与发送数字序列完全相同。信息论得出的重要结论是:对于一个有噪信道,只要在信道编码中引入足够而有限的冗余度,或等价地说编码速率足够小,就能通过信道渐近无误地传送消息。更确切地说,对充分长的数字序列,其接收错误概率可以任意小。信道编码问题是要找出使信道渐近无误地传输消息所能达到的最大编码速率R和相应的编码。已经证明,对于离散无记忆恒参信道,这个最大极限编码速率为
信道编码器将数字序列每K个一组变换为字长N 的信号(码字),称为分组编码。若数字和信道符号都是二进制的(可用0,1表示),则R=K/N 定义为编码速率,它表明每个信道符号表示多少个数字。N-K 称为编码冗余度。信道编码(纠错编码)的基本思想就是增加冗余度以提高可靠性。更确切地说,信道译码器可以利用编码冗余度将受扰信号变换为正确的发送数字序列。重复编码乃一简例。信道编码器将输入数字重复三次, 如将01011变换为000111000111111。信道译码器可用门限译码,即先将输入译码器的信道符号每三个一组地相加,再将结果逐个与阈值 2比较,小于阈值2的译为0,否则译为1。这样若受扰信号010110100011011虽然错了 5个符号,但译码仍为01011与发送数字序列完全相同。信息论得出的重要结论是:对于一个有噪信道,只要在信道编码中引入足够而有限的冗余度,或等价地说编码速率足够小,就能通过信道渐近无误地传送消息。更确切地说,对充分长的数字序列,其接收错误概率可以任意小。信道编码问题是要找出使信道渐近无误地传输消息所能达到的最大编码速率R和相应的编码。已经证明,对于离散无记忆恒参信道,这个最大极限编码速率为![]() ,它是对X上一切概率分布 p取极大值。p为信道转移概率(条件概率),
,它是对X上一切概率分布 p取极大值。p为信道转移概率(条件概率),