论文记载：FRAP：Learning Phase Competition for Traffic Signal Control

ABSTRACT

一个为早晨的交通训练好的模型可能不适用于下午的交通，因为交通流可能被逆转，导致非常不同的状态表示。本文基于交通信号控制中相位冲突的直观原理，提出了一种新的设计方案FRAP:当两个交通信号发生冲突时，优先考虑交通流量较大(即需求较高)的信号。通过相位冲突建模，我们的模型实现了对交通流中翻转、旋转等对称情况的不变对称性。

1 INTRODUCTION

以前的RL方法[Coordinated Deep Reinforcement Learners for Traffic Light Control.，Reinforcement Learning Approach for Intelligent Traffic Light Control]都是独立地从8个方向独立的输入，回归Q(s，a)值，即，由于它们必须在每个状态上尝试八种动作，因此大约需要\((8 ×n^8) × 8\)个样本来获得满意的近似。但事实上，相当一部分状态-动作对是不必要探究的。以图1为例。这两种情况大致是镜像(流量翻转)。这种翻转是人们早上从住宅区通勤到商业区，下午反向交通的常见现象。由于这样的翻转将导致现有方法的完全不同的状态表示，已经了解第一种情况的RL代理仍然不能处理第二种情况。但是根据常识，这两种情况几乎是相同的，人们希望从第一种情况中学习的模型可以处理第二种情况或其他类似的情况。此外，如图2所示，给定任何特定的状态，可以通过旋转和翻转生成七个其他案例。因此，即使在训练期间只看到一个案例，理想的RL模型也能处理所有八个案例，具有一定的泛化能力。

基于上述观察，我们提出了一个新的模型设计称为FRAP，它是不变的对称操作，如翻转和旋转，并考虑所有相位置。关键的想法是，与其考虑单个的交通时刻如关注不同交通运动之间的时刻。这个想法是基于交通信号控制中冲突的直观原理:

• (1)较大的交通流量表明对绿色信号的需求较高；
• (2)当两个交通流冲突时，我们应该优先考虑需求较高的一个。

受此原理启发，FRAP首先预测每个信号相位的需求，然后对相位之间的冲突进行建模。通过成对相位冲突建模，FRAP可以在交通信号控制中实现对对称性的不变性(例如翻转和旋转)。通过利用这种不变性并实现跨对称状态的知识共享，FRAP成功地将勘探空间从\(64 ×n^8\)样本减少到\(16×n^4\)样本(详细分析见第4节)。与现有的基于RL的方法相比，FRAP在复杂场景下找到了更好的策略，收敛速度更快。请注意，我们的模型设计独立于强化学习技术的最新进展，包括不同的算法，如基于值的方法[Distributed Prioritized Experience Replay]，基于策略的方法[Asyn-chronous methods for deep reinforcement learning. ]，以及神经网络设计或训练技巧，如Double DQN [Deep reinforcementl earning with double q-learning]，Dueling network[Dueling network architectures for deep reinforcement learning.]。因此，我们的方法可以与这些算法或技巧相结合，以获得更好的性能。然而，这些不在本文讨论范围之内。因此，为了集中验证我们设计的有效性，我们使用了最新的先进的Ape-X DQN [Distributed Prioritized Experience Replay]作为我们模型设计的基础。

总之，本文的主要贡献包括:

• 提出了一种新的基于强化学习的交通信号控制模型设计框架FRAP。通过捕捉不同信号相位之间的冲突关系，该算法实现了对对称性的不变性，从而更好地解决了困难的全相位交通信号控制问题。
• 我们所展示的FRAP框架在通过真实世界数据的综合实验的学习过程中收敛速度比现在的RL算法要快的多。
• 我们进一步证明了FRAP的优越的延展性。更特别的是，我们证实了FRAP能够处理不同的道路结构，不同的交通流，真实世界中复杂的相位设置，以及多交叉环境。

2 RELATED WORK

传统交通信号控制。交通信号控制是交通领域的核心研究课题，现有的方法一般可分为四类：

• 定时控制根据人类的先验知识决定交通信号计划，但是信号灯不会定时根据实时数据而改变。
• 选取动作方法定义为一系列规则，并且根据预定义的规则和实时数据触发交通信号。一个规则可以是，如果队列长度大于某个阈值，则为该方向移动设置绿色信号灯
• 基于选择的自适应控制方法首先决定一组交通信号计划，并为当前交通状况(例如，从环路传感器接收的交通量数据)选择最佳计划。这种方法在今天的交通信号控制中得到广泛应用。常用的系统包括SCATS ，RHODES 和SCOOT

上述所有方法都高度依赖人类知识，因为它们需要手动设计的交通信号计划或规则。基于优化的自适应控制方法较少依赖人工知识，根据观测数据来决定交通信号方案。这些方法通常将交通信号控制表述为特定交通流模型下的优化问题。

为了使优化问题易于处理，通常会对模型做一些强有力的假设。例如，一个经典的方法是通过假设一致的到达率来优化交通。然后可以使用基于交通数据的公式来计算包括周期长度和相位比的交通信号计划。然而，模型假设统一的到达率经常受到太多的限制，并且不适用于现实世界。

交通信号控制学习。与传统方法不同，基于学习的交通信号控制不需要预先定义的交通信号计划或交通流模型。特别是RL方法直接从与世界的交集中学习。在这些方法中，每个交叉口是一个智能体，状态是对该交叉口交通状况的描述，行动是交通信号，奖励是对交通效率的衡量。

现有的RL方法在环境的状态描述(例如，车辆位置的图像[6，18，32，38，40]，队列长度[1–3，38，40]，等待时间[7，28，38，39，41])，动作定义(例如，改变到下一相位，28，32，38]，设置相位，2，8，30])和奖励设计(例如，队列长度[6，22，32，36])方面有所不同就算法而言，研究已经利用了针对离散状态空间的表格方法(例如，Q-learning[3，12])和approximation methods[19，38]，这些方法可以进一步分类为value based的方法(例如，deep Q-Network[19，32，38])、policy based(例如，policy gradient[27])和actor critic [4，5，9]。

然而，据我们所知，由于状态空间大，这些方法都没有在单个交叉口的完整8相位方案中显示出令人满意的结果。本文遵循交通信号控制中冲突和对称性的普遍原理，设计了一种新的高效探索模型。此外，我们采用Ape-X DQN [16]的分布式框架作为我们的基础框架，该框架被显示为在玩雅达利游戏时实现最先进的性能。但是我们的模型设计可以适用于其他算法框架，包括policy-based和基于actor-critic的强化学习方法。

3 PROBLEM DEFINITION

3.1 Preliminary

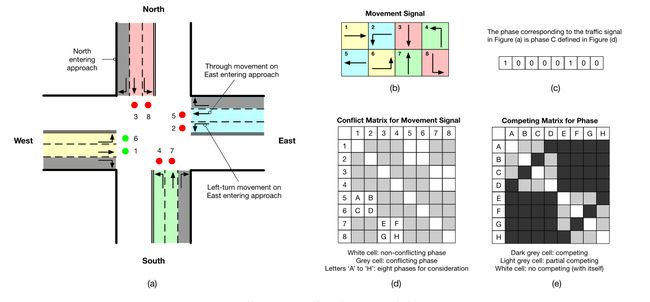
本文研究了单交叉口和多交叉口的交通信号控制。为了说明这些定义，我们使用图3中所示的4路交叉口作为例子。但是这些概念可以容易地推广到不同的交叉路口结构(例如，不同数量交叉路口)。

• Entering approach:每个路口有四个进路，分别命名为北/南/西/东进路(简称‘N’、‘S’、‘W’、‘E’)。在图3(a)中，我们指出了向北进入的方法。
• Traffic movement:交通时刻被定义为向某个方向移动的交通，即左转、直行和右转。在图3(a)中，我们显示有8个由信号控制的交通时刻(不包括右转)。遵循大多数国家的交通规则，无论信号如何，右转交通都可以通过，但需要在红灯时让步。此外，交通时刻可能会占用一个以上的车道，但这并不影响我们的模型设计，因为交通信号控制的是交通时刻，而不是车道。
• Movement signal: 对于每个交通移动，我们可以使用一个变量，1表示“绿色”信号，0表示“红色”。
• Phase: 我们使用一个8bit 容器p来表示交通时刻信号的组合(即相位)，如图3(c)所示。图3(d)中的信号灯冲突矩阵所示，一些信号灯不能同时变成变成“绿色”(例如，信号#1和#2)。所有非冲突信号将产生8个有效的成对信号相位(图3(d)中的字母“A”至“H”)和8个单信号相位(冲突矩阵中的对角线单元)。(图3(d)中A，代表1号口5号口同时开放)。这里我们不考虑单信号相位，因为在一个孤立的交叉口，使用成对信号相位总是更有效。

说到相位的关系(图3(e))，总共有两类:冲突和部分冲突。部分冲突相位如，“A”和“B”)有一个共同的流量移动，而冲突相位没有。(“A”相位是1,5号口开放，“B”相位是2,5号口开放，5号口是共同的流量移动，没有冲突，1,2号口现实中只能开放一个，是有冲突的，所以“A”，“B”是部分冲突)在建模中应该区别对待它们(详见第4节)。

3.2 RL Environment

在反馈学习思想的驱动下，本文提出了一种交通信号控制的强化学习方法。在我们的问题中，一个智能体可以观察一个孤立的十字路口的交通状况(图3(a))并相应地改变交通信号。该智能体的目标是学习一种优化交通时间的信号操作策略。这个交通信号控制问题可以表述为一个马尔可夫决策过程\(< S，A，P，R，γ >\)

问题1。给定状态观测集\(S\)，动作集\(A\)，奖励函数\(R\)是\(S × A → \mathbb R\)的函数，具体来说，\(R^a_s= \mathbb E[R_{t+1}|S_t= s，A_t= a]\)。智能体的目的就是学习一个策略\(\pi(A_t= a|S_t= s)\)，该策略确定在给定状态\(s\)下采取的最佳行动\(a\)，从而使以下总折扣回报最大化:

\[G_t=R_{t+1}+\gamma R_{t+2}+\gamma ^2 R_{t+3}+\cdots=\sum_{m=0}^{\infty}\gamma^m R_{t+m+1} \tag1 \]

对于交通信号控制，我们的RL智能体定义如下:

• State: 每个交通时刻 \(i\) 的车辆数量 \(f_i^v\) 和当前交通信号相位(在容器中表示为每个交通时刻信号的1 bit \(f_i^s\))。上面的v和s分别代表车辆(vehicles)和信号(signal)。

• Action: 为下一个时间间隔选择相位。

• Reward: 每个交通时刻的平均队列长度。

请注意，我们使用了一组相对简单的状态特征和奖励函数，因此我们在本文中重点创新了模型设计。在[43]中，优化队列长度已被证明等同于优化交通时间(交通中最广泛接受的衡量标准)。此外，简洁的状态设计也被证明是有效的[43]。同时，我们的方法可以很容易地结合更复杂的状态特征和对性能提升的奖励。

4 METHOD

4.1 Model Overview

我们使用Ape-X Deep Q-learning (DQN) 来解决RL 问题，神经网络将交通时刻的状态特征作为输入，预测每个动作(即相位)的得分(即Q值)，可以描述为Bellman Equation[31]:

\[Q(s_t,a_t) = R(s_t,a_t) +γ maxQ(s_{t+1},a_{t+1}). \tag 2 \]

在这一步中选取最高回报的动作。

我们基于两个普遍原则设计了一个名为FRAP的新网络(它对翻转和旋转等对称操作不变，并考虑了所有的相位配置) 冲突原则：

• Principle of competition: 交通流量越大，对“绿色”交通信号的要求就越高。当两个信号冲突时，应优先考虑需求较高的信号。
• Principle of invariance(对称性): 信号控制应该不受旋转和翻转等对称性的影响。

这样，通过更新相同的网络模块(即参数)，现在可以同时对不同的交通时刻和相位进行学习，这导致更有效地使用数据样本和更好的性能。

本节的其余部分组织如下。在第4.2节中，我们简要概述了最先进的Ape-X DQN [16]框架，我们的方法就是建立在这个框架之上的。然后，我们在第4.3节中详细描述了我们的网络设计。在第4.4节中，我们进一步讨论了我们模型的一些重要性质。

4.2 Algorithmic Framework

为了提高在大的搜索空间中的学习效率，我们采用分布式框架Ape-X DQN [16]作为我们的算法框架。在Ape-X DQN中，标准的深度强化学习被分解为两部分: \(acting\) 和 \(learning\) 。行动部分分配具有不同探索策略的多个行动者与环境交互，并将观察到的数据存储在经验回放存储器中。学习部分负责对经验回放存储器中的训练数据进行采样，以更新模型。最重要的是，这两个部分可以同时运行，同时保持生成和消耗训练数据的速度几乎相等。简而言之，受益于高探索和采样效率，该框架可以显著提升强化学习的学习性能。关于Ape-X DQN的更多细节，我们请感兴趣的读者参考[16]。

4.3 Phase Invariant Signal Control Design

正如我们之前所讨论的，由于搜索空间大，训练一个用于交通信号控制的RL智能体极具挑战性。例如，对于图3(a)所示的四车道交叉路口，假设每次交通移动只有一条车道，状态空间的大小就会是\(8 ×n^8\) ，其中n是车道的容量。因此，即使通道容量很小 (例如, n = 10), DQN将需要数十亿个数据样本来了解state、action和reward之间的关系。此外，交叉口的几何形状(例如，3、4或5个进入入口)和信号设置(即，交通时刻信号的不同组合)可能不同。如果需要为每个不同的交叉路口学习不同的智能体，效率非常低。

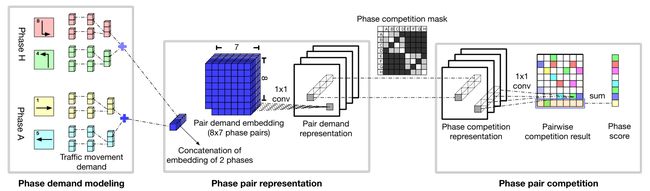
为了应对这些挑战，我们基于第4.1节中概述的两个原则来设计我们的模型，这样它就可以更有效地从数据中学习，并且可以很容易地适应不同的交叉路口结构。我们将相位得分(即Q值)的预测分为三个部分：相位需求建模、相位对表示和相位对冲突。图4显示了我们的方法的概述，图5显示了详细的网络参数设置。接下来，我们详细描述设计。

4.3.1 Phase Demand Modeling.(相位需求建模)

在这个阶段，我们的目标是获得每个信号相位的需求表示。回想一下，对于任何交通时刻 \(i，i\in\{ 1，...，8\}\)，其状态包括车辆数量和当前信号相位。这些特征可以直接从模拟器中获得。我们先拿这两个特征分别表示为 \(f^v_i\) 和 \(f^s_i\) 的两个特征，作为输入，并通过两个全连接层的神经网络传递它们，以生成对该交通时刻 \(d_i\) 的“绿色”信号灯需求的表示。

\[h^v_i= ReLU(W^vf^v_i+ b^v),\;\;\;\;\;\; h^s_i= ReLU(W^sf^s_i+ b^s). \tag 3 \]

\[d_i= ReLU(W^h[h^v_i,h^s_i] + b^h). \tag 4 \]

请注意，在通过输出层之前，两个隐藏层向量 \(h^v_i、h^s_i\) 是组合在一起的。此外，神经网络的学习参数在所有交通时刻之间共享。最终我们通过将 \(p\) 中两个不冲突的交通时刻信号的需求相加，得到任意 p 相位的需求表示：

\[d(p) = d_i+ d_j, where\;\; p_i= p_j= 1. \tag 5 \]

4.3.2 Phase Pair Representation. (相位对表示)

根据冲突原则，一个阶段的得分(优先级)取决于它与其他阶段的冲突。因此，对于每个相位 \(p\) ，我们形成相位对 \((p，q)\) ，其中 \(q\) 与 \(p\) 不是同一种相位，(即 \(q\neq p\) )。给定一个相位对 \((p，q)\) 和它们的需求大小，我们这个阶段的目标是获得 \(p\) 和 \(q\) 之间冲突的表示。

相位对需求全连接方块 \(D\) (图4中的蓝色方块)是通过首先连接所有相位对中的相位的需求表示( 即 \([d(p)，d(q)]\) )，然后收集所有相位对的向量而形成的。对于我们的 8 相位问题，\(D\) 的大小是 \(8 × 7 ×l_1\)，其中 \(l_1\) 是单个相位对的需求全连接向量的长度。

然后，我们进一步在 \(D\) 上应用 \(K\) 个带 \(1 × 1\) 滤波器的卷积层，得到相位对需求表示。第 \(k\) 层可以写成\(Eq. (6)\)，\(H^d_0= D\)。

\[H^d_k= ReLU(W^d_k· H^r_{k−1}+ b^d_k) \tag 6 \]

\(1×1\) 滤波器的选择遵循通过让它们相互作用来提取相位对中的关冲突系的思想，这在先前的工作中得到验证[20]。\(1 × 1\) 滤波器还支持不同相位对之间的参数共享。因为不同相位对(例如，2、3、4或更多相位对)之间没有显式的有意义的相互作用，所以使用较大的滤波器是没有用的。

4.3.3 Phase competition mask.(相位对冲突掩盖矩阵)

为了更好地理解，这一部分在图4中用灰色矩阵表示，但在图5中有详细描述。如图3(e)所示，相位对p和q可以有两种不同的关系：部分冲突(例如浅灰色的 'A' 和 'B' 相位中，有一个交通时刻信号灯是冲突的，图3中1号信号灯和2号信号灯冲突)，全冲突(例如深灰色的 'A' 和 'D' 相位中，它们完全相互冲突)。一旦确定了相位对，我们的模型将查找相位冲突矩阵，并将关系映射到全连接向量 \(e(p，q)\) 。将所有相位对的全连接向量放在一起形成关系全连接体 \(E\) 。类似于对需求表示建模，在 \(E\) 上应用 \(K\) 个带\(1×1\) 滤波器的卷积层，得到对相位对的关系掩盖。第 \(k\) 层可以写成 \(Eq.(7)\)，\(H^r_0= E\)。

\[H^r_k= ReLU(W^r_k· H^r_{k−1}+ b^r_k) \tag 7 \]

4.3.4 Phase Pair Competition.(相位对冲突)

在这一阶段，我们的模型将相位对需求表示和相位冲突掩盖作为输入，并考虑到每个相位与其他相位的竞争，预测每个相位的得分(即Q值)。

在最后一个阶段之后，相位竞争表示 \(H^c\) 可以通过相位对需求表示 \(H^d_K\) 和相位冲突掩盖 \(H^r_K\) : \(H^c= H^d_K⊗ H^r_K\)的逐元素乘法来获得。然后，我们应用另一个具有\(1 × 1\)滤波器的卷积层来获得成对冲突结果矩阵 \(C\)，其中的每一行表示相位 \(p\) 相对于其所有相位的相对优先级。从数学上讲，我们有

\[C = ReLU(W^c· H^c+ b^c). \]

最后，将每个相位p的相对优先级相加，得到相位 \(p\) 的得分。然后，我们的RL智能体选择得分最高的相位作为其动作。

4.3.5 Summary of FRAP network. (FRAP 网络结构总结)

总之，我们在图5中给出了FRAP网络的详细描述，这与图4中的模型设计是一致的。网络主要由全连接层和卷积层组成。在卷积层，滤波器是1×1卷积，步长为1。默认情况下，我们在每个卷积层使用20个过滤器，除了最后一个。

4.4 Discussions

4.4.1 Invariance of our model design.

在上述建模过程中，无论我们关注哪个相位 \(p\) ，我们总是对它与其他相位的关系有一个对称的看法。这使 \(FRAP\) 能够利用交通信号控制中的对称性，并大大减少样本的探索。具体来说，假设每次相位允许的最大车辆数为 \(n\) 。注意，交通相位信号可以是‘1’(绿灯)或者是 '0' (红灯)，如图4所示，我们的网络首先从具有 \(2^2×2^n\) 种可能组合的两个交通相位的特征中获得一个相位的表示。然后，将两个相位配对在一起进行竞争，相位竞争模型在所有的相位对之间共享，这样，为了回归所有8个action的Q值，模型只需要观察 \((2^2×n^2) × (2^2×n^2) = 16 ×n^4\) 组样本，与 \(DRL\) 的\(64×n^8\)[32]和 \(IntelliLight\) [38]相比有显著下降。在第5节中，我们进一步进行了广泛的实验，以说明 \(FRAP\) 收敛更快，并获得更好的解，因为增强的样本效率补偿了状态空间的激增。

4.4.2 Adaption to different environments.

当我们在整个模型设计中关注相位冲突和不变性的普遍原则时，\(FRAP\) 模型可以应用于不同的交通状况(即，小、中和大交通量)，不同的交通信号设置(例如，4相位、8相位)和不同的道路结构(例如，如图6所示的3、4和5-引道交叉口，以及在每次交通运动中具有可变车道数的交叉口)。此外，\(FRAP\) 可以从一个环境中学习，并以高精度转移到另一个环境，而无需任何额外的培训。我们在实验中进一步说明了这一点。

4.4.3 Applications in multi-intersection environments.

虽然我们的讨论到目前为止只集中在单个交叉口上，但 \(FRAP\) 对城市范围内的交通信号控制做出了根本性的贡献，因为单个交叉口的良好学习模型是城市范围内交通信号控制的基础单元。此外，我们证明，即使没有明确的协调，\(FRAP\) 在多交叉环境中也能很好地工作(见实验)。

5 EXPERIMENT

5.1 Experiment Settings

遵循交通信号控制研究[38]的传统，我们在模拟平台 CityFlow 中进行实验，该平台是为大规模交通信号控制设计的开源交通模拟器[42]。模拟器以交通数据作为输入，车辆根据模拟设置行驶到目的地。模拟器可以为交通信号控制方法提供交通状况的观察，并执行信号控制动作。类似于现实世界，每个绿色信号后设置一个3秒的黄色信号和一个2秒的全红色信号。

在交通数据集中，每辆车被描述为 \((o，t，d)\) ，其中 \(o\) 是起点位置，\(t\) 是时间，\(d\) 是终点位置。位置 \(o\) 和 \(d\) 都是道路网上的位置。交通数据作为模拟器的输入。

在多交叉口网络设置中，我们使用真实的道路网络来定义模拟器中的网络。对于单个交叉口，除非另有规定，否则道路网络设置为四向交叉口，有四个300米长的路段。

5.2 Datasets

我们使用来自中国济南和杭州的两个私有真实世界数据集，以及来自美国亚特兰大的一个公共数据集。济南：我们从济南的合作者那里收集十字路口附近监控摄像头的数据。共有7个交叉口，单个交叉口控制的摄像机记录相对完整。该数据集中的每条记录都包含摄像机位置、一辆车到达十字路口的时间以及车辆信息。这些记录是通过先进的计算机技术从摄像机记录中恢复出来的。在我们的实验中，我们在记录的到达时间将车辆送到十字路口。

杭州：该数据集由杭州市2018年4月1日至2018年4月30日的监控摄像机采集。总共有6个路口有相对完整的摄像记录。这些记录的处理与济南的数据类似。

亚特兰大：2006年11月8日，八台摄像机从佐治亚州亚特兰大桃树街的主干道上采集了这些公共数据集。该车辆轨迹数据集提供了研究区域内每辆车的精确位置，总共考虑了五个交叉口。

5.3 Methods for Comparison

为了评估我们模型的有效性和效率，我们将它与以下经典和最新的方法进行比较。我们分别调整每种方法的参数，并获得的最佳性能。

• Fixedtime [23]:固定时间控制采用预先确定的周期和阶段时间计划，广泛应用于稳定的交通流中。进行网格搜索以找到最佳周期。
• SOTL [11]:自组织交通灯控制是一种基于等待车辆数量的手动调节阈值自适应调节交通灯的方法。

• Formula：该方法根据交通状况计算出合理的交通信号周期长度，即均匀交通流的预设流量。然后分配给每个阶段的时间由交通量比率决定。
• DRL [32]：该方法利用DQN框架进行交通灯控制，并以描述车辆在道路上的位置的图像作为状态。
• IntelliLight [38]：这是另一种深度强化学习方法，具有更复杂的网络架构。这是最先进的反向链路方法，在两相信号控制中表现出良好的性能。
• A2C [10]：该方法采用最先进的优势评价框架，利用等待时间和车辆数量来描述交通状态。

5.4 Parameter Settings

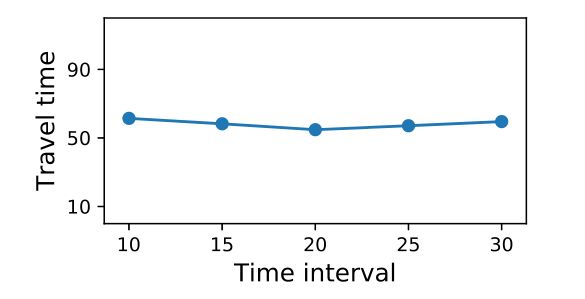
为了训练我们的模型，一些超参数被调整为最佳性能。我们采用了学习率为 \(1e-3\) 的 \(Adam\) 优化器。对于每一轮训练，从存储器中采样1000个状态转换，并以 \(batch\) 大小 \(20\) 进行训练。三个 actor 并行运行以实现 Ape-X DQN 框架。对于两个连续动作之间的时间间隔，我们进行了一个简单的实验，发现模型性能对这个参数不敏感。如图7所示，出行时间受时间间隔影响不大。因此，我们只是按照最近一部作品[14]中的建议将其设置为10秒。

5.5 Evaluation Metrics

基于现有的交通信号控制的研究，我们选择了一个有代表性的指标，交通时间，以供评估。该指标被定义为车辆在接近车道上花费的平均行驶时间(以秒为单位)，这是在交通领域判断性能最常用的衡量标准。

5.6 Overall Performance

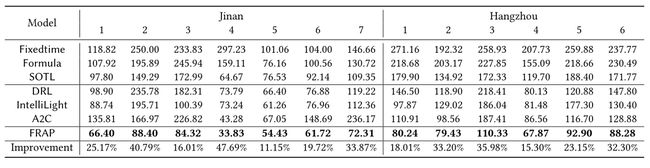
表1和表2报告了采用8阶段设置的所有方法实现的行驶时间。请注意，改进是FRAP超过最佳基线的百分比。我们可以清楚地看到，我们的方法在所有数据集上都明显优于所有其他方法。

正如预期的那样，RL方法往往比固定时间等传统方法表现更好，因为在交叉点捕获实时信息的能力使反向传播方法能够做出更合理的决策。在这些RL方法中，我们的方法不仅在交通时间方面，而且在收敛速度方面都很突出。图8绘制了RL方法的收敛曲线，FRAP有最快的收敛(由于空间限制，我们只显示了一种情况)。这是因为FRAP利用交通信号控制的对称性和Ape-X DQN框架来提高采样效率。

5.7 Model Characteristics

5.7.1 Invariance to flipping & rotation

除了实现更快的旅行时间和收敛速度，FRAP还有另一个优势，它对翻转和旋转的不变性。在现实世界中，人们早上以特定的运动方式开车上班，下午以相反的方向回家是很常见的。图9显示了济南4号交叉口的交通流翻转示例。可以观察到，上午8点左右，西引道的交通量远大于东引道。下午5点，关系颠倒了。

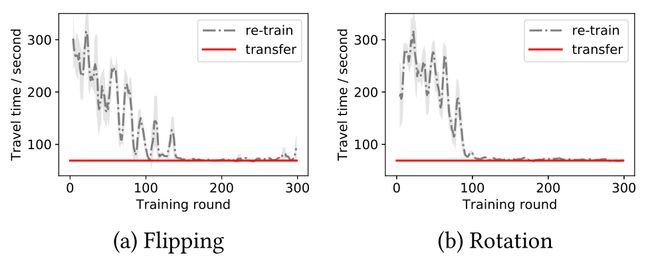
在没有使用交通信号控制的对称性的情况下，先前的RL方法必须在流量剧烈变化(例如翻转和旋转)时重新训练模型。然而，FRAP模型设计保证了我们的方法不太容易受到这种极端变化的影响，这意味着该模型在这些流量下的性能几乎相同。图10显示了FRAP对翻转和旋转的不变性。在这个实验中，我们直接从原始交通流中获取一个训练好的模型，并在翻转和旋转的交通流中进行测试。我们将它的性能与两个重新训练的模型进行比较。从这个图中，我们可以观察到，我们转移的模型实现了与重新训练的模型几乎相同的旅行时间性能，因此节省了额外的训练成本。

5.7.2 Adaptation to different traffic volumes.

在这个实验中，我们说明了FRAP相对于其他RL方法的另一个优点，即它对交通量的适应性。直观地说，如果一个模型在大交通量上训练时探索了足够的状态，它可以适应那些相对较小的交通量。然而，由于大的状态空间，现有的RL方法很难看到足够的样本来传输到不同的交通流。同时，FRAP模型设计利用交通信号控制的对称性来提高数据效率，从而获得更好的可传输性。

在本实验中，我们选择了济南市两个车流量最大的交叉口 2 训练的 FRAP 和 IntelliLight 模型，并评价了它们在交叉口 1 相对较小的交通流下的性能。在这种情况下，两个模型都探索了相似的状态，并收敛到它们可以为交叉点2实现的最佳值。从图11中，我们可以看到FRAP的转移模型与重新训练的模型表现几乎相同，而IntelliLight的重新训练模型和转移模型之间有明显的差距。这表明，所提出的FRAP模型设计显著提高了采样效率，并有助于适应不同的交通流。

5.7.3 Flexibility of the 8-phase setting.

由于交通传统，在现实世界中，四相位设置(相位A、相位D、相位E和相位H)的交叉口也很常见。虽然四相位设置有时简单而有效，但它有一个严重的限制，即在两种相反的方向中，直行或左转信号的绿灯时间总是相同的(左右直行时间总是相同的，当左边直行车多，右边没有直行的车时，就容易产生负面影响)。当这两种方法中的交通量不平衡时，这将对行驶时间产生负面影响，这在实际道路上经常发生。与此同时，8相位设置允许车辆有一种专门通过的方法。在本实验中，我们表明8相位设置比4相位设置更灵活，即在8相位设置下，车辆可以更快、更合理地通过。

如图12所示，当济南1号交叉口西、东进车流量相差较大时，8相位设置下学习到的策略可以相应调整绿灯时间，而4相位设置下的策略浪费了大量时间在车流较少的运动上(如东进车辆交通)。事实上，在8相位设置下，行驶时间仅为66.40秒，但在4相位设置下，行驶时间增加到81.97秒。因此，一般的8相位设置为交通信号控制带来了灵活性，因为它能更好地适应不平衡的交通流。

5.8 Experiment on Different Environments

5.8.1 Experiment on different intersection structures.

我们还评估了我们的方法在不同交叉口结构下的性能(即3、4和5个交叉口)。在本实验中，我们根据济南市交通流的均值和方差，为每个结构合成了一个典型的交通流。

我们修改我们的模型如下。对于三向交叉，我们禁用网络中的一些神经元，使其与该结构兼容。此外，对于不存在的移动，使用零填充来修改输入。对于5-道路结构，我们向模型中添加另一个阶段，然后使用与图4中相同的过程(即相位需求建模、相位对全连接和相位对冲突)来预测所有阶段的Q值。

不同交叉结构的详细结果见表3。我们可以看到，FRAP的性能始终优于其他方法，并且可以轻松地应用于所有结构，而无需进行重大修改。

5.8.2 Extension to a multi-intersection environment.

与单个交叉口相比，人们有时更关心包含多个交叉口的区域的整体交通灯控制。在多路口环境中实现智能交通灯控制的一种简单方法是为每个路口分配一个独立的RL智能体。

为了验证我们的模型在多交叉口环境中的潜力，我们分别在济南、杭州和亚特兰大选取了一个3 × 4、一个4 × 4和一个1 × 5的交叉口网格。济南和杭州数据选自数据覆盖面相对丰富的地区。进行必要的缺失数据填充，对数据进行预处理。不同方法的性能如表4所示。我们可以看到，在这种设置下，FRAP再次在所有交通信号控制方法中脱颖而出。为了进一步改进，相邻交叉口的协调可以被认为是未来工作的一个有前途的方向。

5.9 Interpretation of Learned Policies

为了进一步了解FRAP学到了什么，我们选择了一个交叉点，并以以下方式可视化学到的策略:对于一天中最繁忙的时间上午8点至晚上8点之间的每个小时，我们根据特定的策略计算分配给每个交通方向的绿灯时间，然后对其进行归一化，以获得绿灯时间百分比。同时，我们计算每次交通的车辆数比，以供参考。

如图13所示，FRAP的绿灯时间比率与每小时的交通量百分比很好地同步，而其他基线方法，如SOTL和DRL，会更随机和不规则地为每个运动分配绿灯时间。具体来说，在选定的时间段内，四次左转运动的车辆流量与四次直行运动相比相对较轻。因此，一个好的政策应该是给贯穿运动分配更多的绿色时间。图13显示，FRAP确实将直行和左转运动分为两组，而SOTL和DRL基本上将它们混合在一起。

6 CONCLUSION

本文从冲突性和对称性的普遍原理出发，提出了一种新的用于交通信号控制的RL模型FRAP。我们分析了FRAP相对于其他RL方法在采样效率上的优势，并在三个数据集上进行了综合实验。实验结果表明，该方法收敛速度快，性能优于现有方法。此外，我们展示了我们的模型在处理复杂场景(如不同的交叉路口结构和多交叉路口环境)方面的潜力。对于未来的工作，行人和非机动车辆的模式需要考虑，实地研究可以是我们的模型获得真实世界的反馈和验证所提出的RL的重要一步。

7 ACKNOWLEDGMENTS

这项工作得到了国家自然科学基金#1652525、#1618448和#1639150奖项的部分支持。本文包含的观点和结论是作者的观点和结论，不应被解释为代表任何资助机构。

REFERENCES

[1] Monireh Abdoos, Nasser Mozayani, and Ana LC Bazzan. 2011. Traffic light control in non-stationary environments based on multi agent Q-learning. In Intelligent Transportation Systems (ITSC), 2011 14th International IEEE Conference on. IEEE, 1580–1585.
[2] Monireh Abdoos, Nasser Mozayani, and Ana LC Bazzan. 2014. Hierarchical control of traffic signals using Q-learning with tile coding. Applied intelligence 40, 2 (2014), 201–213.
[3] Baher Abdulhai, Rob Pringle, and Grigoris J Karakoulas. 2003. Reinforcement learning for true adaptive traffic signal control. Journal of Transportation Engi-neering 129, 3 (2003), 278–285.
[4] Mohammad Aslani, Mohammad Saadi Mesgari, Stefan Seipel, and Marco Wiering. 2018. Developing adaptive traffic signal control by actor–critic and direct exploration methods. In Proceedings of the Institution of Civil Engineers-Transport. Thomas Telford Ltd, 1–10.
[5] Mohammad Aslani, Mohammad Saadi Mesgari, and Marco Wiering. 2017. Adaptive traffic signal control with actor-critic methods in a real-world traffic network with different traffic disruption events. Transportation Research Part C: Emerging Technologies 85 (2017), 732–752.
[6] Bram Bakker, M Steingrover, Roelant Schouten, EHJ Nijhuis, LJHM Kester, et al. Cooperative multi-agent reinforcement learning of traffic lights. (2005).
[7] Tim Brys, Tong T Pham, and Matthew E Taylor. 2014. Distributed learning and multi-objectivity in traffic light control. Connection Science 26, 1 (2014), 65–83.
[8] Vinny Cahill et al. 2010. Soilse: A decentralized approach to optimization of fluctuating urban traffic using reinforcement learning. In Intelligent Transportation Systems (ITSC), 2010 13th International IEEE Conference on. IEEE, 531–538.
[9] Noe Casas. 2017. Deep Deterministic Policy Gradient for Urban Traffic Light Control. arXiv preprint arXiv:1703.09035 (2017).
[10] Tianshu Chu, Jie Wang, Lara Codecà, and Zhaojian Li. 2019. Multi-Agent Deep Reinforcement Learning for Large-Scale Traffic Signal Control. IEEE Transactions on Intelligent Transportation Systems (2019).
[11] Seung-Bae Cools, Carlos Gershenson, and Bart D’Hooghe. 2013. Self-organizing traffic lights: A realistic simulation. In Advances in applied self-organizing systems. Springer, 45–55.
[12] Samah El-Tantawy and Baher Abdulhai. 2010. An agent-based learning towards decentralized and coordinated traffic signal control. In Intelligent Transportation Systems (ITSC), 2010 13th International IEEE Conference on. IEEE, 665–670.
[13] Samah El-Tantawy and Baher Abdulhai. 2012. Multi-agent reinforcement learning for integrated network of adaptive traffic signal controllers (MARLIN-ATSC). In Intelligent Transportation Systems (ITSC), 2012 15th International IEEE Conference on. IEEE, 319–326.
[14] Samah El-Tantawy, Baher Abdulhai, and Hossam Abdelgawad. 2013. Multiagent reinforcement learning for integrated network of adaptive traffic signal controllers (MARLIN-ATSC): methodology and large-scale application on downtown Toronto. IEEE Transactions on Intelligent Transportation Systems 14, 3 (2013),1140–1150.
[15] Martin Fellendorf. 1994. VISSIM: A microscopic simulation tool to evaluate actuated signal control including bus priority. In 64th Institute of Transportation Engineers Annual Meeting. Springer, 1–9.
[16] Dan Horgan, John Quan, David Budden, Gabriel Barth-Maron, Matteo Hessel, Hado van Hasselt, and David Silver. 2018. Distributed Prioritized Experience Replay. CoRR abs/1803.00933 (2018).
[17] PB Hunt, DI Robertson, RD Bretherton, and M Cr Royle. 1982. The SCOOT online traffic signal optimisation technique. Traffic Engineering & Control 23, 4 (1982).
[18] Lior Kuyer, Shimon Whiteson, Bram Bakker, and Nikos Vlassis. 2008. Multiagent reinforcement learning for urban traffic control using coordination graphs. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 656–671.
[19] Xiaoyuan Liang, Xunsheng Du, Guiling Wang, and Zhu Han. 2018. Deep reinforcement learning for traffic light control in vehicular networks. arXiv preprint arXiv:1803.11115 (2018).
[20] Min Lin, Qiang Chen, and Shuicheng Yan. 2013. Network in network. arXiv preprint arXiv:1312.4400 (2013).
[21] PR Lowrie. 1992. SCATS–a traffic responsive method of controlling urban traffic. Roads and traffic authority. NSW, Australia (1992).
[22] Patrick Mannion, Jim Duggan, and Enda Howley. 2016. An experimental review of reinforcement learning algorithms for adaptive traffic signal control. In Autonomic Road Transport Support Systems. Springer, 47–66.
[23] Alan J. Miller. 1963. Settings for Fixed-Cycle Traffic Signals. Journal of the Operational Research Society 14, 4 (01 Dec 1963), 373–386.
[24] Pitu Mirchandani and Larry Head. 2001. A real-time traffic signal control system: architecture, algorithms, and analysis. Transportation Research Part C: Emerging Technologies 9, 6 (2001), 415–432.
[25] Pitu Mirchandani and Fei-Yue Wang. 2005. RHODES to intelligent transportation systems. IEEE Intelligent Systems 20, 1 (2005), 10–15.
[26] Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Tim-othy Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. 2016. Asyn-chronous methods for deep reinforcement learning. In International conference on machine learning. 1928–1937.
[27] Seyed Sajad Mousavi, Michael Schukat, and Enda Howley. 2017. Traffic light con-trol using deep policy-gradient and value-function-based reinforcement learning. Intelligent Transport Systems (ITS) 11, 7 (2017), 417–423.
[28] Tong Thanh Pham, Tim Brys, Matthew E Taylor, Tim Brys, Madalina M Drugan, PA Bosman, Martine-De Cock, Cosmin Lazar, L Demarchi, David Steenhoff, et al. Learning coordinated traffic light control. In Proceedings of the Adaptive and Learning Agents workshop (at AAMAS-13), Vol. 10. IEEE, 1196–1201.
[29] Roger P Roess, Elena S Prassas, and William R McShane. 2004. Traffic engineering. Pearson/Prentice Hall.
[30] As’ ad Salkham, Raymond Cunningham, Anurag Garg, and Vinny Cahill. 2008. A collaborative reinforcement learning approach to urban traffic control optimization. In Proceedings of the 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology-Volume 02. IEEE Computer Society,
560–566.
[31] Richard S Sutton and Andrew G Barto. 1998. Reinforcement learning: An introduction. Vol. 1. MIT press Cambridge.
[32] van der Pol et al. 2016. Coordinated Deep Reinforcement Learners for Traffic Light Control. NIPS.
[33] Hado Van Hasselt, Arthur Guez, and David Silver. 2016. Deep reinforcement learning with double q-learning. In Thirtieth AAAI Conference on Artificial Intel-ligence.
[34] Ziyu Wang, Tom Schaul, Matteo Hessel, Hado Van Hasselt, Marc Lanctot, and Nando De Freitas. 2015. Dueling network architectures for deep reinforcement learning. arXiv preprint arXiv:1511.06581 (2015).
[35] FV Webster and BM Cobbe. 1966. Traffic Signals. Road Research Technical Paper 56 (1966).
[36] Hua Wei, Nan Xu, Huichu Zhang, Guanjie Zheng, Xinshi Zang, Chacha Chen, Weinan Zhang, Yanmin Zhu, Kai Xu, and Zhenhui Li. 2019. CoLight: Learning Network-level Cooperation for Traffic Signal Control. arXiv preprint arXiv:1905.05717 (2019).
[37] Hua Wei, Guanjie Zheng, Vikash Gayah, and Zhenhui Li. 2019. A Survey on Traffic Signal Control Methods. arXiv preprint arXiv:1904.08117 (2019).
[38] Hua Wei, Guanjie Zheng, Huaxiu Yao, and Zhenhui Li. 2018. IntelliLight: A Reinforcement Learning Approach for Intelligent Traffic Light Control. In ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD).
2496–2505.
[39] MA Wiering. 2000. Multi-agent reinforcement learning for traffic light control. In Machine Learning: Proceedings of the Seventeenth International Conference (ICML’2000). 1151–1158.
[40] Lun-Hui Xu, Xin-Hai Xia, and Qiang Luo. 2013. The study of reinforcement learning for traffic self-adaptive control under multiagent markov game environment. Mathematical Problems in Engineering 2013 (2013).
[41] Nan Xu, Guanjie Zheng, Kai Xu, Yanmin Zhu, and Zhenhui Li. 2019. Targeted Knowledge Transfer for Learning Traffic Signal Plans. In Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, 175–187.
[42] Huichu Zhang, Siyuan Feng, Chang Liu, Yaoyao Ding, Yichen Zhu, Zihan Zhou, Weinan Zhang, Yong Yu, Haiming Jin, and Zhenhui Li. 2019. CityFlow: A Multi-Agent Reinforcement Learning Environment for Large Scale City Traffic Scenario. In The World Wide Web Conference. ACM, 3620–3624.
[43] Guanjie Zheng, Xinshi Zang, Nan Xu, Hua Wei, Zhengyao Yu, Vikash Gayah, Kai Xu, and Zhenhui Li. 2019. Diagnosing Reinforcement Learning for Traffic Signal Control. arXiv preprint arXiv:1905.04716 (2019).