【通俗易懂】从贝叶斯公式到卡尔曼滤波
0x00 序言
本人能力有限，文章有错误还请大佬指出。
卡尔曼滤波是为了解决贝叶斯滤波无穷积分无法求的解析解，而对贝叶斯滤波作假设，使得可以通过复变的留数定理或者傅里叶变换+卷积去算，所以我们想要学好卡尔曼滤波就要先学习贝叶斯滤波。
本文相关公式不做推导，适合想要快速理解kalman的同学学习。
0x01 贝叶斯滤波
2.1 贝叶斯公式
贝叶斯滤波是二维连续随机变量的贝叶斯公式的应用算法，贝叶斯公式是概率论中的一个定理，描述在已知一些先验知识和观测数据下，某事件的发生概率。
这里给出结论：
- 二维离散型随机变量的贝叶斯公式：
二维离散型随机变量的贝叶斯公式可通过作图的方式证得。
- 二维连续型随机变量的贝叶斯公式：
为后验概率密度函数，
为似然概率密度函数，
为先验概率密度函数，其中（X|Y）为二维连续型随机变量，x，y位其上的一个取值，二维连续型随机变量的贝叶斯公式的推导较为复杂，在此不做推导。
因为Y=y跟定的情况下，
与x的取值无关，所以将
写作归一化常量
.
所以可以将连续随机变量的贝叶斯公式写作:
后验概率 = 先验概率*似然概率*
其中归一化常量为
2.2 先验概率，似然概率，后验概率
- 先验概率：先验概率又被称作先测概率，是根据过去的经验判断事件发生的概率。
- 似然概率：似然概率是根据观测值判断事件发生的概率。
- 后验概率：后验概率是根据先验概率和似然概率推断出的事件发生的概率。
举个栗子：
数学考试刚刚结束，你平时学习很差，所以你根据以往的经验认为这次考好的概率不大，但是你感觉这次发挥不错，所以你认为这次考试有可能考的不错，你将以上两方面的信息在脑海中融合，最终得出考的不好不差的概率大一些
在这个栗子里，你根据以往经验得出的考好概率就是先验概率，你根据考试时观测到的感受得出的考好概率就是似然概率，最后你将这两个概率在脑海中融合出的考好概率就是后验概率。
2.3 似然概率模型
世界上不存在绝对精确的传感器，如果你的传感器绝对精准的话你也不会来看这篇文章了。
例如一个ToF传感器误差是±0.02m，它的观测值如果为z，则真实的状态量在z-0.02到z+0.02之间，在贝叶斯滤波中，似然概率密度函数表征传感器精度，对于给定的状态条件 X=x，观测结果 Y=y 的概率分布通常有三种模型：
- 等可能型：
在传感器误差范围之内，似然概率密度函数值为一个常数c，在传感器误差范围之外似然概率密度函数值为0，大致图像函数如
这种模型简单，但是往往并不贴近实际模型
- 阶梯型
阶梯型是等可能型的拓展，中间高两边低。
- 正态分布型
这个是重中之重，卡尔曼滤波器使用的似然概率模型就是正态分布型，
此时似然概率模型为高斯函数： 
其中x为传感器观测值，
为传感器精度。
2.4 数据融合
若同时假定先验概率密度函数为高斯函数，即：
则
由
， 
可知，数据融合后方差变小，说明数据精度提高
2.4.1多传感器数据融合公式
直接上结论（推导比较复杂，感兴趣可以自己推导推导试试）：
有N个传感器，第n个传感器的观测值
，其中x为状态的真实值，
为该传感器的测量精度，则
最优估计值: 
2.5 系统建模
k时刻系统状态量随机变量
，k时刻观测量随机变量
，k时刻过程噪声随机变量
，k时刻观测噪声随机变量
，分别有状态方程和观测方程:
其中
为状态转移函数，
为观测函数
贝叶斯滤波的目标是求出k时刻最优估计值，既状态量随机变量的后验概率密度函数的期望：
![\hat{x}_k=E[f_{X_k}^+(x)]](http://img.e-com-net.com/image/info8/e8f54c5671ed4563ba0fbe6a193365c5.gif)
对于 0 时刻的初始状态量随机变量 
，认为观测值 
即为其真值，其后验概率密度函数即为其先验概率密度函数。我们可以根据经验知识（建模精度和传感器精度）写出 0 时刻的初始状态量随机变量 的后验概率密度函数
、k 时刻过程噪声随机变量 的概率密度函数 
和 k 时刻观测噪声随机变量 的概率密度函数 
。
2.6 贝叶斯滤波过程
1.设初值
初始 0 时刻状态量随机变量 的后验概率密度函数：
2.预测
k 时刻状态量随机变量 的先验概率密度函数：
![f_{X_k}^-(x)=\int_{-\infty}^{+\infty}f_{Q_k}[x-f(v)]f_{X_{k-1}}^+(v)\mathrm{d}v](http://img.e-com-net.com/image/info8/193a534936de4590b23dfe2c8d8df178.gif){kind=small}
3.更新
k 时刻状态量随机变量的后验概率密度函数：
![f_{X_{k}}^{+}(x)=\eta_k\cdot f_{R_k}[y_k-h(x)]\cdot f_{X_k}^-(x)](http://img.e-com-net.com/image/info8/b1506a23e19643709fb2b1b0b62fa4a8.gif){kind=small}
归一化常数
:
![\eta_k=\frac{1}{\int_{-\infty}^{+\infty}f_{R_k}[y_k-h(x)]f_{X_k}^-(x)\mathrm{d}x}](http://img.e-com-net.com/image/info8/99a1ccd356da45edbd81dc17b66720f5.gif){kind=small}
4.求解最优估计值
![\hat{x}_k^+=E[f_{X_k}^+(x)]=\int_{-\infty}^{+\infty}xf_{X_k}^+(x)\mathrm{d}x](http://img.e-com-net.com/image/info8/8f58b8911e924e6b967707a57d47deb7.gif){kind=small}
5.开始下一轮递归
0x02 卡尔曼滤波
3.1 卡尔曼滤波的由来
可以看到，贝叶斯滤波在
求解先验概率密度函数时
、求解归一化常数时
、求解最优估计时
都涉及无穷积分，大部分情况无法求的解析解，使得贝叶斯滤波很难实际应用，针对这个问题，主要有以下解决方法
由图可知卡尔曼滤波是贝叶斯滤波为基础，做了如下假设:
(1) 假设一：状态量服从正态分布
(2) 假设二：观测量服从正态分布
(3) 假设三：过程噪声服从均值为 0 的正态分布
(4) 假设四：观测噪声服从均值为 0 的正态分布
(5) 假设五：状态转移函数为线性函数
其中，
为状态转移比例项，对于单一状态量的卡尔曼滤波中， 为一常数；
为控制比例项，
为控制量，和 的乘积可视为线性状态转移函数中的截距项。在简单的系统中，常常没有控制项 和 。
(6) 假设六：观测函数为线性函数
为观测比例项，对于单一状态量的卡尔曼滤波中，为一常数。
3.2 矩阵形式卡尔曼公式
- 状态量 XX 由随机变量演变为随机向量，随机向量中的每一个分量为一个状态量随机变量。维数为
×1 - 状态转移比例项 FF 演变为矩阵，维数为 ×
- 控制量 演变为矩阵，维数为
×1 - 控制比例项 演变为矩阵，维数为 ×
- 状态量概率密度函数均值
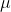演变为矩阵，维数为 ×1 -
状态量概率密度函数方差
不懂协方差矩阵的同学看这里协方差矩阵_百度百科
演变为协方差矩阵，用
表示，维数为 × - 过程噪声方差
演变为协方差矩阵，用
表示，维数为 × - 观测量
由随机变量演变为随机向量，随机向量中的每一个分量为一个观测量随机变量。维数为 
×1 - 观测值 ykyk 由单一值演变为由单一值组成的值矩阵，维数为 ×1
- 观测比例项 演变为矩阵，维数为 ×
- 观测噪声方差
演变为协方差矩阵，用 
表示，维数为 × - 卡尔曼增益系数
演变为矩阵，维数为 ×
卡尔曼滤波五大公式:
即 k 时刻状态量 
的后验估计 
，y
常被称为残差（Residual）或新息（Innovation）；
代表单位矩阵，维数为 ×。
0x03 参考文献
一个例子搞清楚（先验分布/后验分布/似然估计）_你通透就好 别问我是谁的博客-CSDN博客_后验分布
贝叶斯滤波与卡尔曼滤波第七讲 卡尔曼滤波_哔哩哔哩_bilibili
【卡尔曼滤波器】2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题_哔哩哔哩_bilibili
从概率学看卡尔曼滤波_踏雪飞鸿Jaf的博客-CSDN博客
从概率到贝叶斯滤波 | 朝花夕拾
从贝叶斯滤波到卡尔曼滤波 | 朝花夕拾