感知机和BP神经网络
神经网络(Neurual Network) 技术是模仿生物体的神经网络设计而成的，又称人工神经网络(Artificial Neurual Network) ，ANN人工神经网络，模仿生物体的神经网络设计而成。
神经网络既可以用于回归，也可以用于分类。
目录
一、感知机——MLP(BP神经网络)
1，介绍
2，激活函数
1，sigmoid
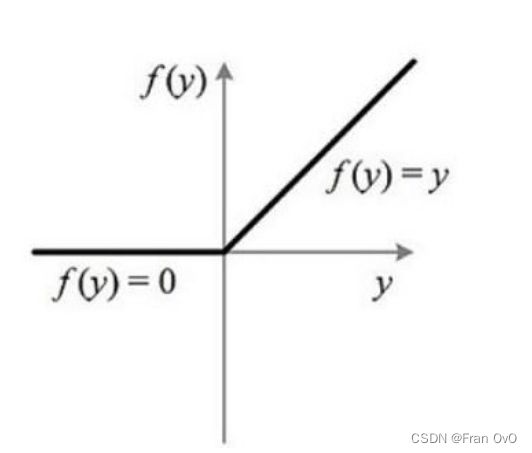
2，relu
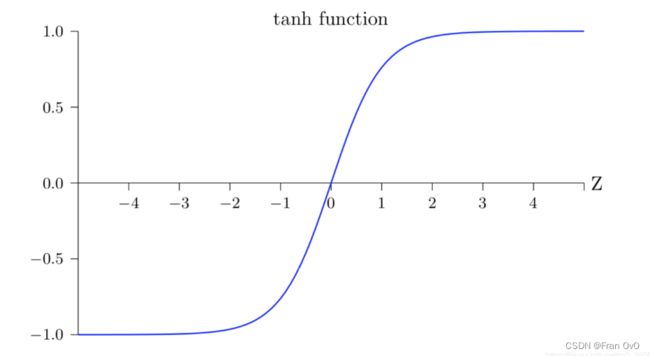
3，tanh
3，BP神经网络结构——多层感知机
4，题目复习
1，eg1
2，eg2
3，eg3
4，eg4
5，eg5
6，eg6
7，eg7
8，eg8
9，eg9
10，eg10
二、感知机的使用
1.导入数据
2.sklearn感知机
3，感知机局限性;
三，神经网络（BP神经网络）
1，sklearn——MLPClassifier
2，手写数字识别
1,获取数据
2，数据预处理
3，利用通道训练手写数据
一、感知机——MLP(BP神经网络)
1，介绍
-
生物上的神经元就是接收四面八方的刺激（输入），然后做出反应（输出），给它一点刺激就灿烂。
- 仿生的ANN一样，整进去一些特征出来一个预测值或者类别。。。
2，激活函数
以西瓜数据为例，我们希望构建一个感知机模型，根据色泽、根蒂、敲声这三个特征，来判断是好瓜还是坏瓜。
感知机模型会将每一个特征值 
乘以一个对应的权重 
，再加上一个偏置 b 。所得到的值如果大于等于 0 ，则判断为 1 类别，即为好瓜；如果得到的值小于 0 ，则判断为 0 类别，即不是好瓜。
其中
为第i个特征值，为第i个特征所对应的的权重，b为偏置。
其中的act函数就是激活函数。
如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。只能对线性数据进行分类：
如果使用激活函数，可以给神经元引入非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中，对非线性数据进行分类：
1，sigmoid
sigmoid 函数是一条平滑的曲线，输出随着输入发生连续的变化。而阶跃函数以 0 为界，输出发生急剧性的变化。 sigmoid 函数的平滑性对神经网络的学习具有重要意义。
1/(1+np.exp(-z))2，relu
sigmoid 函数在 x 过大或过小时，函数变化非常小，即梯度非常接近 0 ，容易产生梯度消失，随着神经网络的加深，在使用梯度下降方法的时候，由于梯度接近 0 ，参数更新接近 0 ，网络开始学不到东西，即梯度消失，对于深度网络训练不太适合。所以现在常使用 relu 激活函数，函数公式如下：
a[a<0]=0
return a3，tanh
tanh为双切正切曲线，过（0,0）点。相比Sigmoid函数，更倾向于用tanh函数
(np.exp(a)-np.exp(-a))/(np.exp(a)+np.exp(-a))3，BP神经网络结构——多层感知机
输入层：信息的输入端，上图中 输入层 只有 1 个节点（一个圈圈），实际的网络中可能有很多个
隐藏层：信息的处理端，用于模拟一个计算的过程，上图中，隐藏层只有三层，节点数为 【3，3，1】 个。
输出层：信息的输出端，也就是我们要的结果，上图中，y 就是输出层的唯一一个节点，实际上可能有很多个输出节点。
权重：连接每层信息之间的参数，上图中只是通过乘机的方式来体现。
4，题目复习
1，eg1
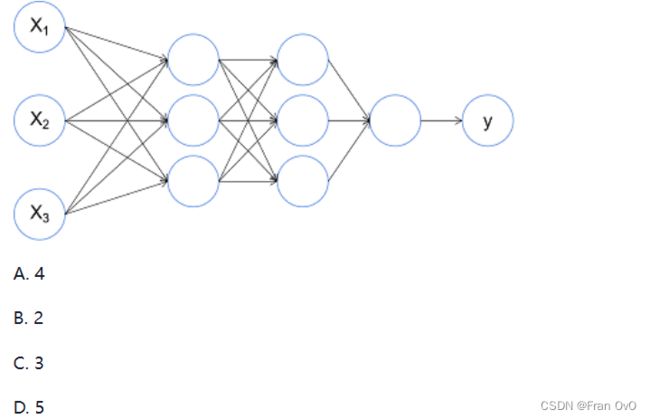
下图是一个神经网络，这个神经网络有多少隐藏层？
A
2，eg2
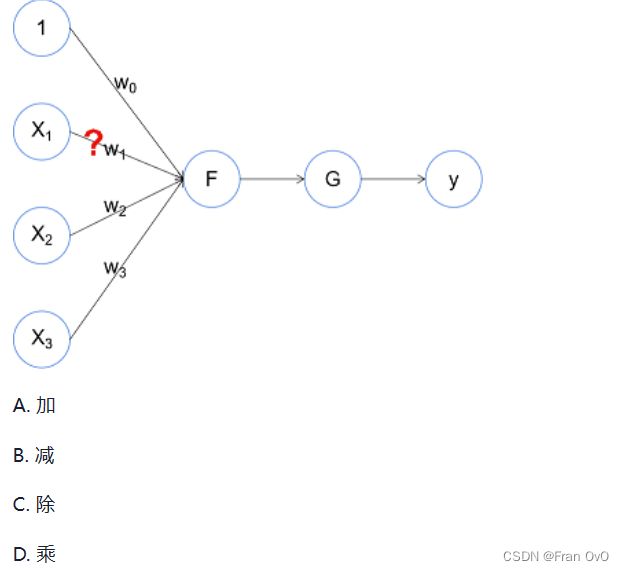
下面是关于感知机的示意图，那么问号处表示x1和w1进行了什么操作？
D.乘
3，eg3
下面是关于感知机的示意图，其中问号的地方数字1表示什么意思？
B，就是个常数项
4，eg4
下面是关于感知机的示意图，其中问号的地方G表示什么功能？
C,激活函数
5，eg5
下图是一个神经网络，这个神经网络有多少参数层？
C,就是全连接之间的权重w，这里由三层参数
6，eg6
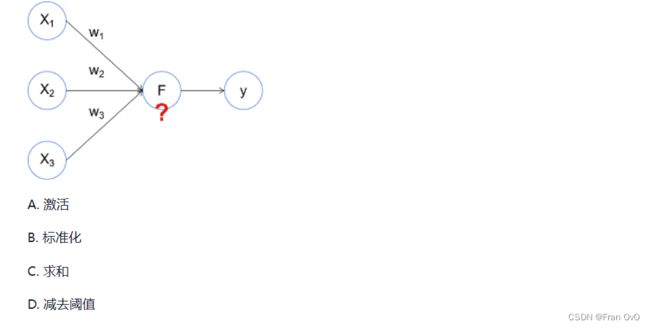
下面是关于感知机的示意图，问号处F应该是一个什么操作？
A，求和
7，eg7
这是经典的感知机模型的示意图。按照这个示意图，图中问号处F单元包括了哪些功能？
ACD
减去阈值就是激活函数的一种，达到阈值则激活
8，eg8
9，eg9
10，eg10
输入——>输出是一个感知机
这就是一个感知机。
题目中可以数出来有7个
二、感知机的使用
1.导入数据
2.sklearn感知机
from sklearn.linear_model import Perceptron
model = Perceptron(penalty='l2',alpha=0.001,max_iter=100)
model.fit(X, y)
model.score(X, y)（linear_model全连接模型）
Perceptron()感知机
参数：
1，penalty：默认=None，即不加惩罚项，‘l2’（L2正则） or ‘l1’（L1正则） or ‘elasticnet’（混合正则）
2，alpha：正则化项需要乘上这个数，在多元回归里面讲过
3，max_iter：最大迭代次数
3，感知机局限性;
X = np.array([[0,0], [1,1], [1,0], [0,1]], dtype=np.float)
y = np.array([0, 0, 1, 1])
model = Perceptron()
model.fit(X, y)
draw_the_model(model, -1, +2)三，神经网络（BP神经网络）
1，sklearn——MLPClassifier
from sklearn.neural_network import MLPClassifier
model = MLPClassifier(solver='adam', activation='relu', hidden_layer_sizes=(10,))
model.fit(X, y)
score = model.score(X, y)
print(f"acc: {score}")参数：
1，hidden_layer_sizes：tuple，length = n_layers - 2，默认值（100，）第i个元素表示第i个隐藏层中的神经元数量。
2，activation：激活函数{‘identity’，‘logistic’，‘tanh’，‘relu’}
默认’relu’ 隐藏层的激活函数：‘identity’，无操作激活，对实现线性瓶颈很有用，返回f（x）= x；
3，slover：{‘lbfgs’，‘sgd’，‘adam’}
’adam’。权重优化的求解器；
'lbfgs’是准牛顿方法族的优化器；
'sgd’指的是随机梯度下降。
2，手写数字识别
1,获取数据
from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data
y = digits.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)2，数据预处理
在神经网络中，数据的预处理非常重要：标准化，归一化
了解量纲：
量纲我觉得最重要的一句话是：物理量的大小与单位有关。
从这句话我们来思考下最核心的两个单词：大小、单位。就是说量纲是有两部分组成：数、单位。就比如1块钱和1分钱，就是两个不同的量纲，因为度量的单位不同了。
1，统计建模中，如回归模型，自变量之间的量纲不一致导致了回归系数无法直接解读或者错误解读；需要将X XX都处理到统一量纲下，这样才可比——去除量纲，统一量纲
2，机器学习任务和统计学任务中有很多地方要用到“距离”的计算，比如PCA，KNN，kmeans等等，假使算欧式距离，不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果——去除量纲，统一量纲
3，参数估计时使用梯度下降，在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。
1，标准化：将数据变换为均值为0，标准差为1的分布切记，并非一定是正态的，
变换后依然保留原数据分布
2，归一化：将一列数据变化到某个固定区间(范围)中，通常，这个区间是[0, 1]，
可以是各种区间，比如映射到[0，1]一样可以继续映射到其他范围，图像中可能会映射到[0,255]，其他情况可能映射到[-1,1]
区别：标准化和归一化本质上都是不改变数据顺序的情况下对数据的线性变化，而它们最大的不同是归一化(Normalization)会将原始数据规定在一个范围区间中，而标准化(Standardization)则是将数据调整为标准差为1，均值为0对分布。
常见归一化和标准化：
1，均值归一化(Mean Normalization)
2，最大最小值归一化(Min-Max Normalization)
3，标准化/z值归一化(Standardization/Z-Score Normalization)
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
std = StandardScaler()#标准化
std_data = std.fit_transform(data)
mm = MinMaxScaler()#归一化
mm_data = mm.fit_transform(data)
3，利用通道训练手写数据
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
p = Pipeline([
('ss', StandardScaler()),#进行标准化
('md', MLPClassifier(solver='adam', activation='relu', hidden_layer_sizes=(150,100))),
])
p.fit(X_train, y_train)
score = p.score(X_test, y_test)
print(f"acc: {score}")