【NumPy库学习】
NumPy库学习
- 1. NumPy数组
- 2. 数据类型
- 3.内存中数组数据的顺序
- 4. 创建数组
-
- 4.1 Meshgrid数组
- 4.2 函数式创建数组
- 5. 数组索引和切片
-
- 5.1 多维数组
- 5.2 数组视图
- 5.3 布尔索引
- 6. 调整形状和大小
- 7. 向量化表达式
-
- 7.1 布尔数组和条件表达式
- 7.2 聚合函数
- 7.3 数组操作
- 8. 矩阵和向量运算
NumPy库(Numerical Python)是Python科学计算环境中最常用的库。它提供了用于处理数组的高效数据结构。Numpy库的核心是使用C语言实现的。
参考资料
NumPy官方网站
在线练习环境
Numpy菜鸟教程
1. NumPy数组
# 为了使用NumPy库,需要先导入它。按照惯例,我们以别名np导入numpy模块。
import numpy as np
NumPy库的核心是表示同质数据的多维数组。数组内所有元素的数据类型是相同的。NumPy中多维数组的主要数据结构是ndarray类(class)。除了保存数组中的数据,这种数据结构还可以包含关于数据的重要描述性的元数据(metaData)。
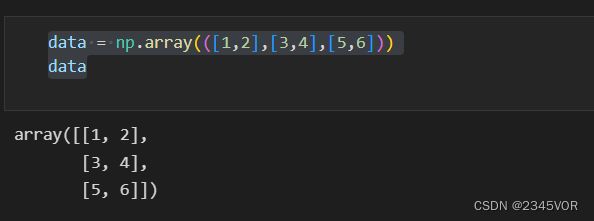
data = np.array(([1,2],[3,4],[5,6]))
data
# 变量类型
print(type(data))
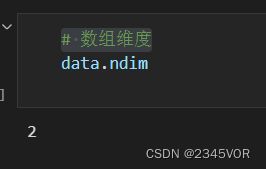
# 数组维度
data.ndim
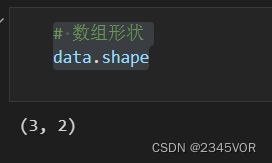
# 数组形状
data.shape
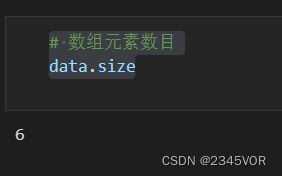
# 数组元素数目
data.size
# 数组元素类型
data.dtype
2. 数据类型
| dtype | 变体 | 说明 |
|---|---|---|
| int | int8, int16, int32, int64 | 整数 |
| unit | unit8, unit16, unit32, unit64 | 无符号整数 |
| bool | bool | 布尔类型 |
| float | float16, float32, float64, float128 | 浮点类型 |
| complex | complex64, complex128, complex256 | 复数浮点类型 |
# 默认数据类型
data = np.array([1,2,3])
print(data.dtype)
# 指定数据类型
data = np.array([1,2,3], dtype=float)
print(data.dtype)
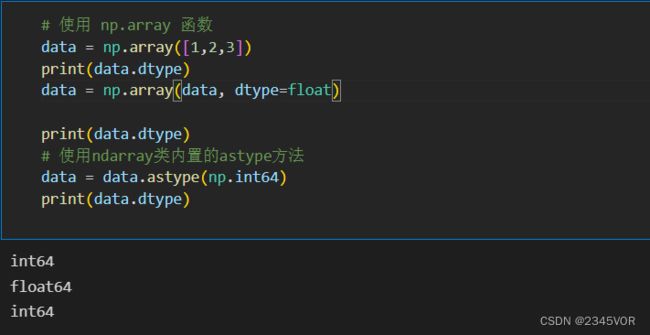
# 使用 np.array 函数
data = np.array([1,2,3])
print(data.dtype)
data = np.array(data, dtype=float)
print(data.dtype)
# 使用ndarray类内置的astype方法
data = data.astype(np.int64)
print(data.dtype)
data = np.array([-1,0,1])
np.sqrt(data)
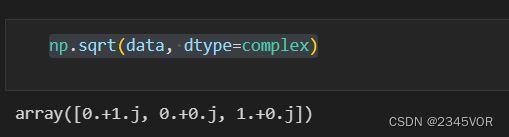
np.sqrt(data, dtype=complex)
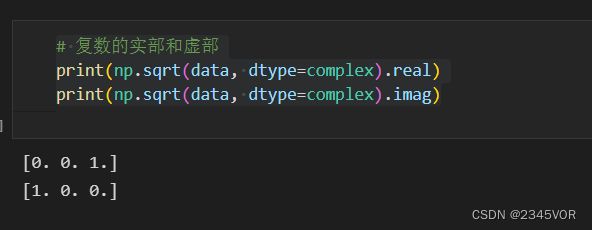
# 复数的实部和虚部
print(np.sqrt(data, dtype=complex).real)
print(np.sqrt(data, dtype=complex).imag)
3.内存中数组数据的顺序
对于包含行列的二维数据:一种可能的方式是按顺序逐行存储数据;一种可能的方式是按列存储数据。前者为行主序(row-major),后者为列主序(column-major)。C语言使用行主序,Fortran和MATLAB使用列主序。
NumPy数组默认使用行主序,创建数组时可以使用关键词参数order='C'或者order='F'设置。当使用借助C或者Fortran编写的接口时,需要特别注意NumPy数组的排序方式。
4. 创建数组
| 函数名 | 说明 |
|---|---|
| np.zeros | 指定维度和类型,以0填充 |
| np.ones | 指定维度和类型,以1填充 |
| np.empty | 未初始化数组 |
| np.arange | 创建均匀间隔数组,指定开始值、结束值和增量值 |
| np.linpace | 创建均匀间隔数组,指定开始值、结束值和元素数量 |
| np.random.rand | 创建一个数组,元素为0-1之间均匀分布的随机数 |
| np.zeros_like | 复制一个数组的维度和类型,以0填充 |
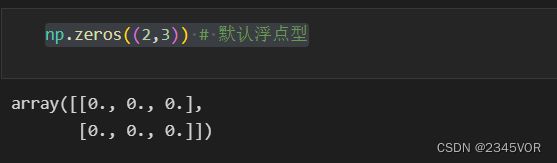
np.zeros((2,3)) # 默认浮点型
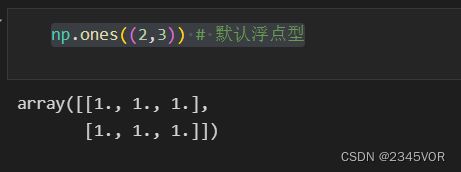
np.ones((2,3)) # 默认浮点型
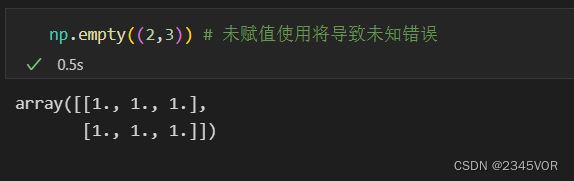
np.empty((2,3)) # 未赋值使用将导致未知错误
# np.arange 不包括结束值
np.arange(0,5,1)
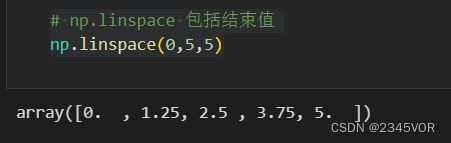
# np.linspace 包括结束值
np.linspace(0,5,5)
4.1 Meshgrid数组
可以使用函数np.meshgrid生成多维坐标网络。
x = np.array([-1, 0, 1])
y = np.array([-2, 0, 2])
X, Y = np.meshgrid(x, y)
print(X)
print(Y)

二维坐标数组的常见应用场景是计算包含两个变量x和y的函数,可以用于绘制包含这两个变量的函数图形,如等高线图。
Z = (X + Y) ** 2
print(Z)
4.2 函数式创建数组
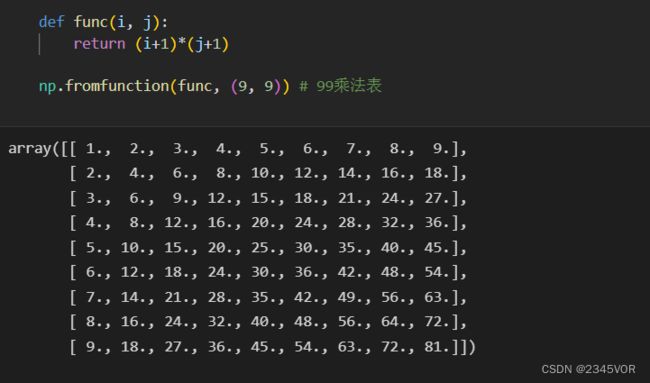
np.fromfunction函数读入多维坐标数组,返回运算结果。
def func(i, j):
return (i+1)*(j+1)
np.fromfunction(func, (9, 9)) # 99乘法表
5. 数组索引和切片
正整数用于从数组开头进行索引(索引开始于0),负整数用于从数组结尾进行索引(索引开始于-1)。
| 函数名 | 说明 |
|---|---|
| a[m] | 选择索引m处的元素,m为整数(从0开始计数) |
| a[-m] | 从数组末尾选择第m个元素,m为负整数(索引开始于-1) |
| a[m:n] | 选择索引为m到n-1的元素 |
| a[:] | 指定维的所有元素,等价为a[0:-1] |
| a[m:n:p] | 选择索引为m到n(不含)的间隔为p的元素 |
| a[::-1] | 逆序选择所有元素 |
a = np.arange(0, 11)
print(a)
print(a[5:])
print(a[::-2])
5.1 多维数组
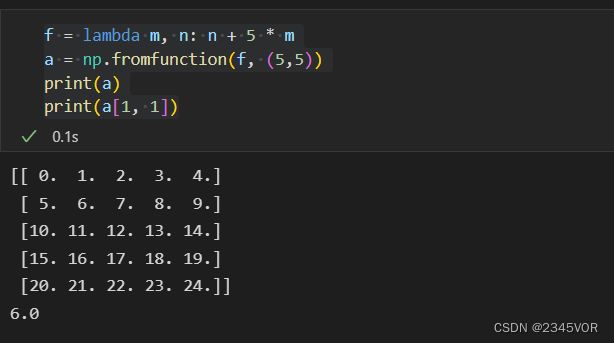
f = lambda m, n: n + 5 * m
a = np.fromfunction(f, (5,5))
print(a)
print(a[1, 1])
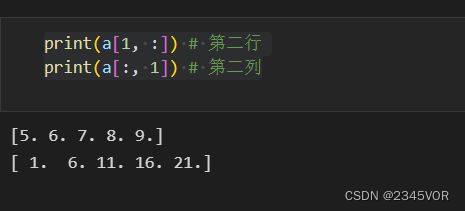
print(a[1, :]) # 第二行
print(a[:, 1]) # 第二列
5.2 数组视图
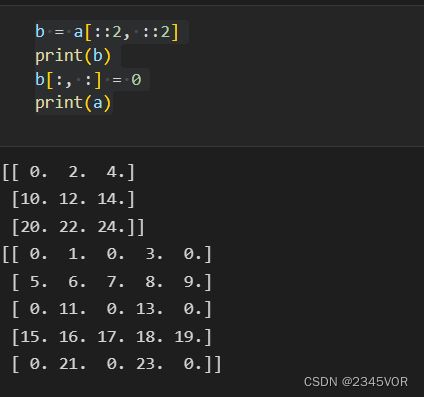
为了提高性能,使用切片操作提取的子数组是内存中同一组数据的不同视图。如果更改视图中的数据,原始数组中的数据也会被修改。如果需要数据的副本,可以使用np.copy()函数。
b = a[::2, ::2]
print(b)
b[:, :] = 0
print(a)
5.3 布尔索引
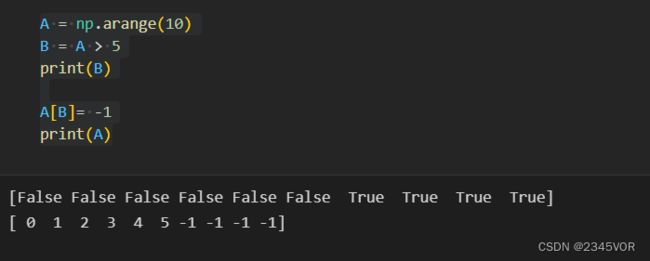
A = np.arange(10)
B = A > 5
print(B)
A[B]= -1
print(A)
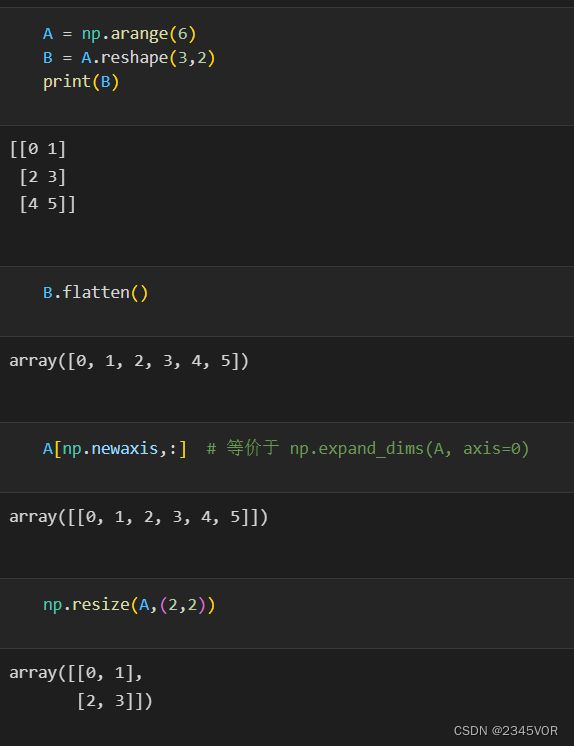
6. 调整形状和大小
| 函数名 | 说明 |
|---|---|
| np.reshape 和 np.ndarray.reshape | 调整N维数组的维度。元素的总数保持不变。 |
| np.resize 和 np.ndarray.resize | 调整N维数组的大小,创建新副本。元素增加则使用原数据填充。 |
| np.ndarray.flatten | 创建N维数组的副本,并折叠成一维数组 |
| np.ndarray.ravel | 创建N维数组的视图,并折叠成一维数组 |
| np.squeeze | 删除长度为1的维度 |
| np.expand_dims 和 np.newaxis | 在数组中增加长度为1的新维度 |
| np.transpose 和 np.ndarray.transpose | 对数组进行转置 |
| np.hstack 和 np.hstack | 对数组进行转水平叠加(沿着轴1)和垂直叠加(沿着轴0) |
| np.append | 在数组中添加元素。该操作会创建一个副本 |
| np.insert 和 np.delete | 在数组中插入和删除元素。该操作会创建一个副本 |
7. 向量化表达式
对标量和数组进行操作,广播会对标量与数组中的每个元素分别进行运算。当两个数组大小不同时,较小的数组通过广播匹配较大的数组。
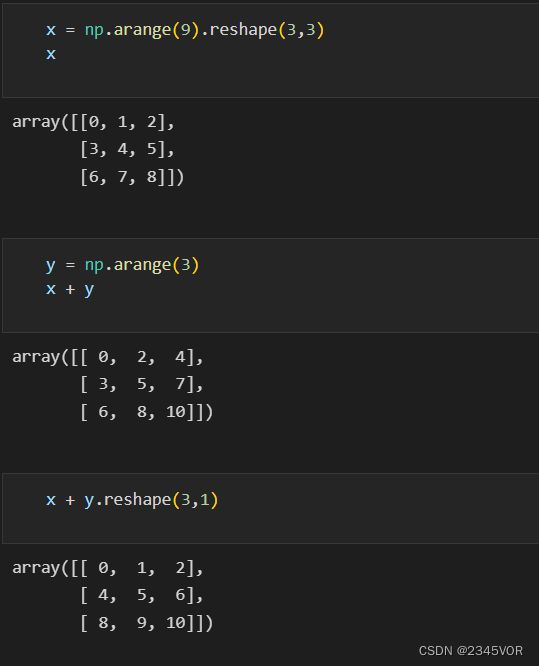
对不兼容大小或形状的数组进行算数运算,则会引发ValueError错误。

7.1 布尔数组和条件表达式
布尔数组和数值数组一起出现时,布尔数组会被转换为数值数组,False和True分别被转换为0和1。

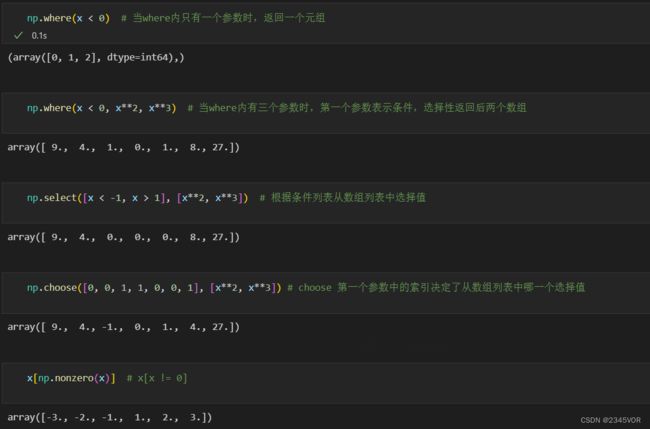
7.2 聚合函数
对数组进行聚合计算,返回一个标量。
| 函数名 | 说明 |
|---|---|
| np.where | 根据条件数组的值从连个数组中选择值 |
| np.choose | 根据给定的索引数组选择 |
| np.select | 根据条件列表从数组中选择 |
| np.nonzero | 返回非0值的索引 |
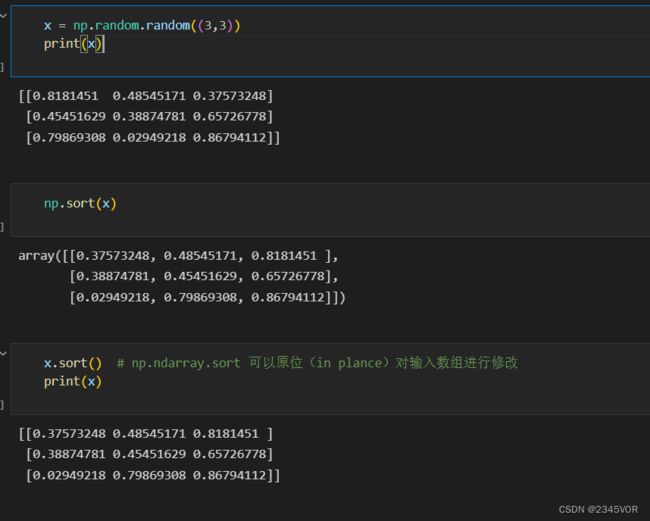
7.3 数组操作
| 函数名 | 说明 |
|---|---|
| np.transpose 和 dp.ndarray.T | 转置 |
| np.fliplr 和 npflipud | 反转每行和每列的元素 |
| np.rot90 | 沿着前两个轴把元素旋转90度 |
| np.sort 和 np.ndarray.sort | 沿着指定轴对元素进行排序 |
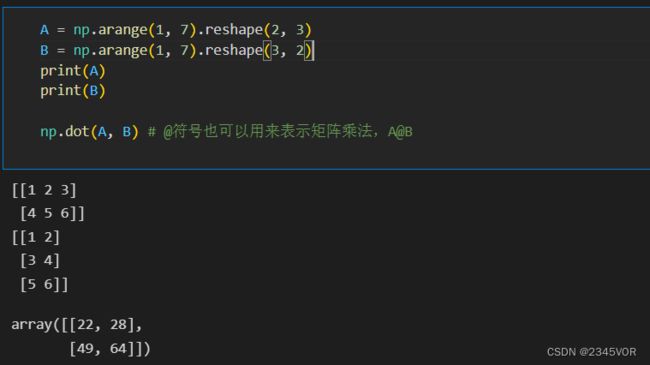
8. 矩阵和向量运算
| 函数名 | 说明 |
|---|---|
| np.dot | 点积 |
| np.inner | 内积 |
| np.cross | 叉积 |
| np.tensordot | 沿着多维数组指定轴进行点积 |
| np.outer | 外积(向量张量积) |
| np.kron | 两个高维数组进行Kronecker积(矩阵张量积) |
| np.einsum | 对多维数组执行爱因斯坦求和约定操作 |
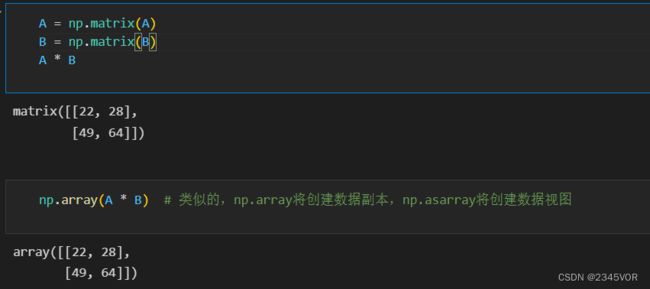
NumPy为ndarray提供另一种数据结构matrix,诸如A * B之类的表达式可以使用matrix乘法表示。逆矩阵表示为 matrix.I,复共轭转置表示为 matrix.H。与np.matrix创建数据副本不同,np.asmatrix函数以np.matrix实例的形式创建原始数组的视图,不增加计算成本。
最后给大家准备一份小册子

参考文献来自桑鸿乾老师的课件:科学计算和人工智能