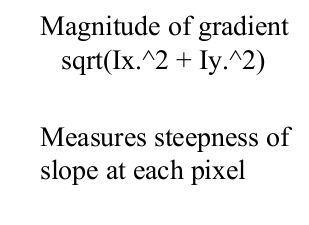opencv轮廓检测之椭圆检测-----算法篇(3)--Sobel

前两篇只是吧水平方向和竖直方向求导进行了线性叠加,

而实际上我们是用梯度大小描述陡峭程度 

#include 

#include 

int main(int argc, char ** argv)

{

    if(argc < 2)

        return -1;

    cv::Mat img = cv::imread(argv[1],0);

    cv::Mat dst1 , dst2, dst3 ,dst;

    cv::Matx33f kernelx(-1,0,1,

                        -2,0,2,

                        -1,0,1);

    cv::Matx33f kernely(-1,-2,-1,

                         0, 0, 0,

                         1, 2, 1);

//    cv::flip(kernelx,kernelx,-1);

//    cv::flip(kernely,kernely,-1);

//    cv::sepFilter2D(img,dst,CV_64F,kernelx,kernely);//kernel.type() == DataType
::type && (kernel.rows == 1 || kernel.cols == 1)) in RowFilter

    cv::filter2D(img,dst1,CV_32F,kernelx);

    cv::filter2D(img,dst2,CV_32F,kernely);

    cv::namedWindow("dst1",cv::WINDOW_AUTOSIZE);

    cv::namedWindow("dst2",cv::WINDOW_AUTOSIZE);

    cv::imshow("dst1",dst1);

    cv::imshow("dst2",dst2);

//    dst3 = dst1 + dst2;

//     cv::convertScaleAbs( dst1, dst1 );

//    cv::convertScaleAbs( dst2, dst2 );

    std::cout << dst1.depth() <<std::endl

              << dst2.depth() << std::endl;

    dst1.convertTo(dst1,CV_32F);

    dst2.convertTo(dst2,CV_32F);

//    addWeighted( dst1, 0.5, dst2, 0.5, 0, dst3 );//dst (I) = saturate ( src1 (I) * alpha + src2 (I) * beta + gamma )

//    cv::magnitude( dst1, dst2, dst3 );   //x – floating-point array of x-coordinates of the vectors.

                                           //y – floating-point array of y-coordinates of the vectors; it must have the same size as x .

                                           // not for 2D image

    cv::pow( dst1, 2, dst1 );

    cv::pow( dst2, 2, dst2 );

    cv::addWeighted( dst1, 1, dst2, 1, 0, dst3 );//dst3= dst1 +dst2;

    cv::sqrt( dst3, dst3);

    cv::filter2D(img,dst,-1,kernelx);

    cv::filter2D(dst,dst,-1,kernely);

    cv::namedWindow("dst3",cv::WINDOW_AUTOSIZE);

    cv::namedWindow("dst",cv::WINDOW_AUTOSIZE);

    cv::imshow("dst3",dst3);

    cv::imshow("dst",dst);

    for(;;)

    {

        if(cv::waitKey(0)==27)

            break;

    }

    return 0;

}

这里将输出像素改为32位浮点数,得到下面

实际上,  将前面两个小节的程序中,  像素深度都改为CV_32F,

效果是一样的.

   看看上面的几幅图,   可见在求导之前滤波有多么重要!

当然,  当应用了二值化,   选择threshold>80

看看效果,   还算可以