dsp复习笔记（奥本海姆离散时间信号处理）

dsp复习

连续时间信号的采样

周期采样

$x[n]=x_c(nT)$

采样的频域表示

$X_s(j\Omega )=\frac{1}{T_s}{\sum }_{k=-\infty }^{+\infty }{X}_c(j\Omega -kj{\Omega }_s)$
不发生混叠的条件：${\Omega }_s>2{\Omega }_N$
采样信号的恢复：一个增益为T的理想滤波器，且满足${\Omega }_N<{\Omega }_c<{\Omega }_s-{\Omega }_N$
奈奎斯特率：$2{\Omega }_N$
离散频率与连续频率的映射关系:$\omega =\Omega T$

由样本重构带限信号

假定${\Omega }_c=\frac{{\Omega }_s}{2}=\frac{\pi }{T}$
重构滤波器：$h_r(t)=\frac{sin\frac{\pi t}{T}}{\frac{\pi t}{T}}$
重构信号在各采样时刻点与原连续信号有着相同的值

连续时间信号的离散时间处理

$H_{eff}(j\Omega )=H(e^{j\Omega T})$ $|\Omega |<\frac{\pi }{T}$

脉冲响应不变

$h[n]=T{h}_c(nT)$
$H(e^{j\omega })=TH(\frac{j\omega }{T})$ $|\omega |\le \pi$

离散时间信号的连续时间处理

实际使用较少，一般用在非整数延迟
$H(e^{j\omega })=H_c(j\frac{\omega }{T})$ $|\omega |\le \pi$

降采样

M倍降采样：$X_d(e^{j\omega })=\frac{1}{M}{\sum }_{i=0}^{M-1}X(e^{j(\frac{\omega -2\pi i}{M})})$
需满足${\omega }_{N}M<\pi$,否则就会混叠
需要在降采样操作前加一个离散时间滤波器

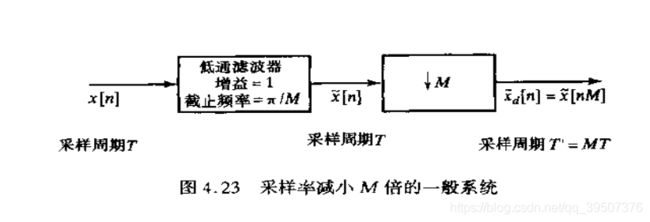
升采样

$X_e(e^{j\omega })=X(e^{j\omega L})$
升采样会产生镜像
镜像滤波器：增益为L，截止频率$\frac{\pi }{L}$

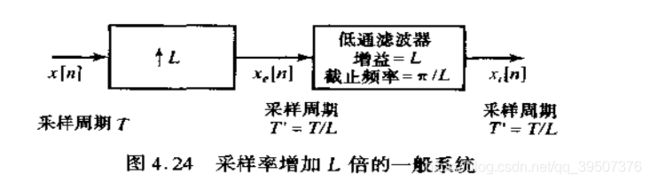
采样率按非整数因子变换

线性时不变系统的变换分析

LTI系统的频率响应

$Y(e^{j\omega })=H(e^{j\omega })X(e^{j\omega })$
幅度和相位满足：
$|Y(e^{j\omega })|=|H(e^{j\omega })||X(e^{j\omega })|$
$argY(e^{j\omega })=argH(e^{j\omega })+argX(e^{j\omega })$

理想选频滤波器

LPF:$h[n]=\frac{sin{\omega }_{c}n}{\pi n}$
HPF:$h[n]=\delta [n]-\frac{sin{\omega }_{c}n}{\pi n}$

群延迟

$\tau (w)=-\frac{d}{d\omega }grd[H(e^{j\omega })]$

线性常系数差分方程表征的系统函数

稳定性：收敛域包括单位圆
因果性：右边序列

逆系统

$H_i(z)=\frac{1}{H(z)}$
逆系统的收敛域必须与原系统有公共部分

如果要求因果稳定系统的逆系统也因果稳定，则所有的零点和极点都必须在单位圆内（最小相位系统）

IIR和FIR

IIR系统：H(z)至少有一个非零极点
FIR系统：没有0和无穷以外的极点

幅度与相位之间的关系

$|H(e^{j\omega }){|}^2=H(e^{j\omega })H^{\ast }(e^{j\omega })=H(z)H^{\ast }(\frac{1}{z^{\ast }})$

全通系统

零点和极点互为共轭倒数
$H(z)=\frac{z^{-1}-a^{\ast }}{1-a{z}^{-1}}$
一般系统可分解为最小相位系统和全通系统的级联，由于全通系统的群延迟大于等于0，因此最小相位系统的群延迟也最小。

最小相位系统

最小相位和全通分解

假设零点$z=\frac{1}{c^{\ast }}$在单位圆外
$H(z)=H_1(z)(1-c{z}^{-1})\frac{z^{-1}-c^{\ast }}{1-c{z}^{-1}}$

频率响应的补偿

$H_d(z)=H_{dmin}(z)H_{ap}(z)$
补偿系统函数$H_c(z)=\frac{1}{H_{dmin}(z)}$

最小相位系统的性质

最小相位滞后，最小群延迟，最小能量延迟

广义线性相位的线性系统

线性相位系统

即理想群延迟
$H_{id}(e^{j\omega })=e^{-j\omega \alpha }$ $|\omega |<\pi$
$\alpha$是实数但不一定是整数

广义线性相位

$H(e^{j\omega })=A(e^{j\omega })e^{-j\alpha \omega +j\beta }$
序列必须对称

因果广义线性相位系统

第I类：M为偶数，偶对称
第II类：M为奇数，偶对称（-1）
第III类：M为偶数，奇对称（-1，1）
第IV类：M为奇数，奇对称（1）

离散时间系统结构

方框图表示

三种基本运算：相加，相乘

IIR

直接I型
直接II型：延迟单元合并
级联型
并联型

FIR

直接型
并联型
线性相位

滤波器设计方法

脉冲响应不变法

$h[n]=T_d{h}_c(n{T}_d)$
$H(e^{j\omega })=H_c(j\frac{\omega }{T_d})$ $|\omega |\le \pi$
$\omega =\Omega T_d$
连续域的极点$s_k$映射到离散域为$e^{s_{k}T}$
能保证线性关系，但可能会混叠，不能用于设计高通滤波器等

双线性变换法

$s=\frac{2}{T_d}\frac{1-z^{-1}}{1+z^{-1}}$
$\Omega =\frac{2}{T_d}\tan \frac{\omega }{2}$
避免了混叠，但是会产生畸变

窗函数法

本质：利用时域乘积，频域卷积的性质
先由最大误差确定窗的种类，再根据主瓣宽度确定窗长

矩形窗可以得到最小的均方逼近

离散傅里叶变换

离散傅里叶级数

$X[k]={\sum }_{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn}$=${\sum }_{n=0}^{N-1}x[n]W_N^{kn}$
$x[n]=\frac{1}{N}{\sum }_{k=0}^{N-1}X[k]W_N^{-kn}$

离散傅里叶级数的性质

线性
$x[n-m]:W_N^{km}X[k]$
$W_N^{-nl}x[n]:X[k-l]$
对偶性
$X[n]:Nx[-k]$
周期卷积
${\sum }_{m=0}^{N-1}{x}_1[m]x_2[n-m]:X_1[k]X_2[k]$
$x_1[n]x_2[n]:\frac{1}{N}{\sum }_{l=0}^{N-1}{X}_1[l]X_2[n-l]$
共轭对称
$x^{\ast }[n]:X^{\ast }[k]$
以及奇部和偶部的对称关系

周期信号

$X(e^{j\omega })={\sum }_{k=-\infty }^{+\infty }\frac{2\pi }{N}X[k]\delta (\omega -\frac{2\pi k}{N})$

有限长序列的离散傅里叶变换

$X[k]={\sum }_{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn}$=${\sum }_{n=0}^{N-1}x[n]W_N^{kn}$
$x[n]=\frac{1}{N}{\sum }_{n=0}^{N-1}X[k]W_N^{-kn}$

离散傅里叶变换的性质

线性
循环移位 $x[((n-m){)}_N]:W_N^{mk}X[k]$
对偶性 $X[n]:x[((-k){)}_N]$
对称性 $x^{\ast }[n]:X^{\ast }[((-k){)}_N]$
循环卷积 ${\sum }_{m=0}^{N-1}{x}_1[m]x_2[((n-m){)}_N]:X_1[k]X_2[k]$
$x_1[n]x_2[n]:\frac{1}{N}{\sum }_{l=0}^{N-1}{X}_1[l]X_2[((k-l){)}_N]$

离散傅里叶变换实现线性卷积

DFT点数大于线性卷积序列长度

DFT实现LTI系统

假定脉冲响应$h[n]$长度为P，$x[n]$的长度远大于P，可以分成长度为L的小段，
重叠相加：
直接将每一段$x_k[n]$补零到L+P-1

重叠保留：每段向前补P-1个点，输入L-P+1个新点

离散傅里叶变换的计算（FFT）

复数乘法：$\frac{N}{2}lo{g}_{2}N$
复数加法： $Nlo{g}_{2}N$
蝶形数目：$\frac{N}{2}$
级数：$lo{g}_{2}N$

按时间抽取的FFT算法

推导过程
$X[k]={\sum }_{n为偶数}x[n]W_N^{kn}+{\sum }_{n为奇数}x[n]W_N^{kn}$
$={\sum }_{r=0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+W_N^k{\sum }_{r=0}^{\frac{N}{2}-1}x[2r+1]W_N^{2rk}$
$=G[k]+W_N^{k}H[k]$
可以分解为两个新的$\frac{N}{2}$点序列
蝶形图：

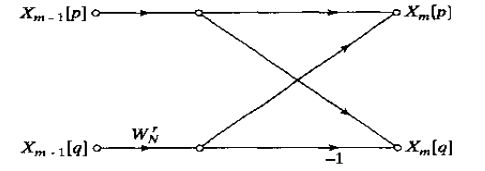
倒序输入，顺序输出（标准情形下，实际可能有变化）

按频率抽取的FFT算法

$X[2r]={\sum }_{n=0}^{N-1}x[n]W_N^{2rn}$
$={\sum }_{n=0}^{\frac{N}{2}-1}x[n]W_N^{2rn}+{\sum }_{n=\frac{N}{2}}^{N-1}x[n]W_N^{2rn}$
$={\sum }_{n=0}^{\frac{N}{2}-1}(x[n]+x[n+\frac{N}{2}])W_{\frac{N}{2}}^{rn}$
同理可得
$X[2r+1]={\sum }_{n=0}^{N-1}x[n]W_N^{2rn}{W}_N^n$
$={\sum }_{n=0}^{\frac{N}{2}-1}(x[n]-x[n+\frac{N}{2}])W_{\frac{N}{2}}^{rn}{W}_N^n$
蝶形图：

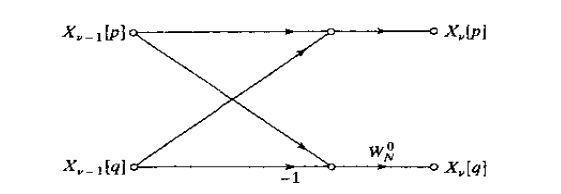
恰好为DIT-FFT的转置

顺序输入，倒序输出

利用离散傅里叶变换的信号傅里叶分析

${\Omega }_k=\frac{2\pi k}{NT}$